1.5: Restar números enteros (Parte 1)
- Page ID
- 114229
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Usar notación de resta
- Modelo de resta de números enteros
- Restar números enteros
- Traducir frases de palabras a notación matemática
- Restar números enteros en aplicaciones
Antes de comenzar, toma este cuestionario de preparación.
- Modelar\(3 + 4\) usando bloques de base diez. Si te perdiste este problema, revisa la Sección 1.2: Agregar números enteros
- Agregar:\(324 + 586\). Si te perdiste este problema, revisa el Ejemplo 1.2.9.
Usar notación de resta
Supongamos que hay siete plátanos en un bol. Elana usa tres de ellos para hacer un batido. ¿Cuántos plátanos quedan en el bol? Para responder a la pregunta, restamos tres de siete. Cuando restamos, le quitamos un número a otro para encontrar la diferencia. La notación que usamos para\(3\) restar\(7\) es
\[7-3 \nonumber\]
Leemos\(7 − 3\) como siete menos tres y el resultado es la diferencia de siete y tres.
Para describir la resta, podemos usar símbolos y palabras.
| Operación | Notación | Expresión | Leer como | Resultado |
|---|---|---|---|---|
| Resta | - | 7 - 3 | siete menos tres | la diferencia de 7 y 3 |
Traducir de la notación matemática a las palabras:
- \(8 − 1\)
- \(26 − 14\)
Solución
- Leemos esto como ocho menos uno. El resultado es la diferencia de ocho y uno.
- Leemos esto como veintiséis menos catorce. El resultado es la diferencia de veintiséis y catorce.
Traducir de la notación matemática a las palabras:
- \(12 − 4\)
- \(29 − 11\)
- Contestar a
-
doce menos cuatro; la diferencia de doce y cuatro
- Respuesta b
-
veintinueve menos once; la diferencia de veintinueve y once
Traducir de la notación matemática a las palabras:
- \(11 − 2\)
- \(29 − 12\)
- Contestar a
-
once menos dos; la diferencia de once y dos
- Respuesta b
-
veintinueve menos doce; la diferencia de veintinueve y doce
Modelo de resta de números enteros
Un modelo puede ayudarnos a visualizar el proceso de resta tanto como lo hizo con la suma. Nuevamente, usaremos\(10\) bloques base. Recuerde que un bloque representa\(1\) y una varilla representa\(10\). Empecemos modelando la expresión de resta que acabamos de considerar,\(7 − 3\).
| Comenzamos modelando el primer número, 7. |  |
| Ahora llévate el segundo número, 3. Daremos un círculo de 3 cuadras para demostrar que nos los estamos llevando. |  |
| Contar el número de bloques restantes. |  |
| Quedan 4 unas cuadras. | Hemos demostrado que 7 − 3 = 4. |
Modelar la resta:\(8 − 2\).
Solución
| 8 − 2 significa la diferencia de 8 y 2. | |
| Modelar el primero, 8. |  |
| Quita el segundo número, 2. |  |
| Contar el número de bloques restantes. |  |
| Quedan 6 unas cuadras. | Hemos demostrado que 8 − 2 = 6. |
Modelo:\(9 − 6\).
- Contestar
-
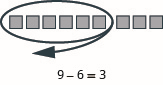
Modelo:\(6 − 1\).
- Contestar
-
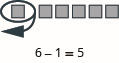
Modelar la resta:\(13 − 8\).
Solución
| Modele el primer número, 13. Utilizamos 1 diez y 3 unos. |  |
| Llévate el segundo número, 8. No obstante, no hay 8, por lo que cambiaremos el 1 diez por 10. |  |
| Ahora podemos llevarnos 8. |  |
| Contar los bloques restantes. |  |
| Quedan cinco. | Hemos demostrado que 13 − 8 = 5. |
Como hicimos con adición, podemos describir los modelos como unos bloques y decenas de varillas, o simplemente podemos decir unos y decenas.
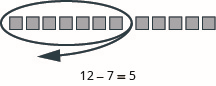
Modelar la resta:\(12 − 7\).
- Contestar
-
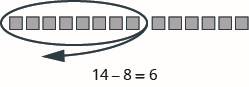
Modelar la resta:\(14 − 8\).
- Contestar
-
Modelar la resta:\(43 − 26\).
Solución
Porque\(43 − 26\) significa\(43\) llevar\(26\), comenzamos por modelar el\(43\).

Ahora, tenemos que llevar\(26\), que son\(2\) decenas y\(6\) unas. No podemos quitarles\(6\) unos a\(3\) unos. Entonces, cambiamos\(1\) diez por\(10\) unos.

Ahora podemos llevarnos\(2\) decenas y\(6\) unas.
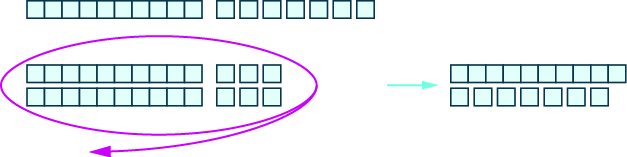
Contar el número de bloques restantes. Hay\(1\) diez y\(7\) unos, que es\(17\).
\[43 − 26 = 17 \nonumber\]
Modelar la resta:\(42 − 27\).
- Contestar
-
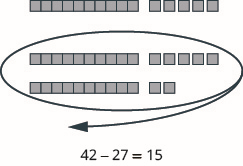
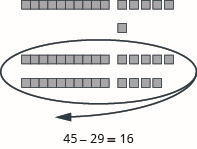
Modelar la resta:\(45 − 29\).
- Contestar
-
Restar números enteros
La suma y la resta son operaciones inversas. La suma deshace la resta y la resta deshace la suma. Sabemos\(7 − 3 = 4\) porque\(4 + 3 = 7\). Conocer todos los hechos del número de suma ayudará con la resta. Entonces podemos verificar la resta sumando. En los ejemplos anteriores, nuestras restaciones se pueden verificar por suma.
\[\begin{split} 7 − 3 = 4 \qquad &\text{because} \qquad 4 + 3 = 7 \\ 13 − 8 = 5 \qquad &\text{because} \qquad 5 + 8 = 13 \\ 43 − 26 = 17 \qquad &\text{because} \qquad 17 + 26 = 43 \end{split}\]
Restar y luego verificar agregando:
- \(9 − 7\)
- \(8 − 3\)
Solución
| 9 - 7 | |
| Resta 7 de 9. | 2 |
| Consultar con adición. 2 + 7 = 9 ✓ |
| 8 - 3 | |
| Resta 3 de 8. | 5 |
| Consultar con adición. 5 + 3 = 8 ✓ |
Restar y luego verificar agregando:\(7 − 0\)
- Contestar
-
\(7-0=7; 7+0=7\)
Restar y luego verificar agregando:\(6 − 2\)
- Contestar
-
\(6-2=4; 2+4=6\)
Para restar números con más de un dígito, suele ser más fácil escribir los números verticalmente en columnas tal como lo hicimos para la suma. Alinea los dígitos por valor posicionar, y luego restar cada columna comenzando por los unos y luego trabajando a la izquierda.
Restar y luego verificar sumando:\(89 − 61\).
Solución
| Escribe los números para que los dígitos unos y diez se alineen verticalmente. | 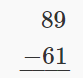 |
|
Restar los dígitos en cada valor posicionar. Restar los unos: 9 - 1 = 8 Restar las decenas: 8 - 6 = 2 |
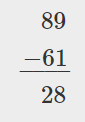 |
| Verifique usando adición. | 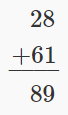 |
Nuestra respuesta es correcta.
Restar y luego verificar sumando:\(86 − 54\).
- Contestar
-
\(86-54=32\)porque\(54+32=86\)
Restar y luego verificar sumando:\(99 − 74\).
- Contestar
-
\(99-74=25\)porque\(74+25=99\)
Cuando modelamos restando\(26\) de\(43\), intercambiamos\(1\) diez por\(10\) unos. Cuando hacemos esto sin el modelo, decimos que tomamos prestado\(1\) del lugar de las decenas y agregamos\(10\) al lugar de unos.
Paso 1. Escribe los números para que cada valor posicional se alinee verticalmente
Paso 2. Restar los dígitos en cada valor posicionar. Trabajar de derecha a izquierda comenzando por el lugar de unos. Si el dígito en la parte superior es menor que el dígito de abajo, tome prestado según sea necesario
Paso 3. Continuar restando cada valor posicional de derecha a izquierda, tomando prestado si es necesario.
Paso 4. Verifique agregando.
Restar:\(43 − 26\).
Solución
| Escribe los números para que cada valor posicional se alinee verticalmente | 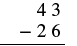 |
| Resta los unos. No podemos restar 6 de 3, así que tomamos prestado 1 diez. Esto hace 3 decenas y 13 unas. Escribimos estos números encima de cada lugar y tachamos los dígitos originales. | 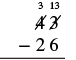 |
| Ahora podemos restar los unos. 13 − 6 = 7. Escribimos el 7 en el lugar de unos en la diferencia. | 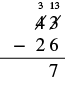 |
| Ahora restamos las decenas. 3 − 2 = 1. Escribimos el 1 en el lugar de las decenas en la diferencia. | 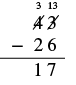 |
| Verifique agregando. | 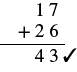 |
Nuestra respuesta es correcta.
Restar y luego verificar sumando:\(93 − 58\).
- Contestar
-
\(93-58=35\)porque\(58+35=93\)
Restar y luego verificar sumando:\(81 − 39\).
- Contestar
-
\(81-39=42\)porque\(42+39=81\)
Restar y luego verificar sumando:\(207 − 64\).
Solución
| Escribe los números para que cada valor posicional se alinee verticalmente | 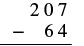 |
| Restar los unos. 7 − 4 = 3. Escribe el 3 en el lugar de unos en la diferencia. Escribe el 3 en el lugar de unos en la diferencia. | 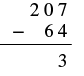 |
| Resta las decenas. No podemos restar 6 de 0 así que pedimos prestado cien y sumamos 10 decenas a las 0 decenas que teníamos. Esto hace un total de 10 decenas. Escribimos 10 por encima del lugar de las decenas y tachamos el 0. Después tachamos los 2 en el lugar de los cientos y escribimos 1 encima de él. | 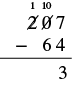 |
| Ahora restamos las decenas. 10 − 6 = 4. Escribimos el 4 en el lugar de las decenas en la diferencia. | 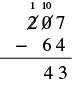 |
| Por último, restar los cientos. No hay dígito en el lugar de cientos en el número inferior así que podemos imaginar un 0 en ese lugar. Desde 1 − 0 = 1, escribimos 1 en el lugar de cientos en la diferencia. | 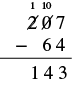 |
| Verifique agregando. | 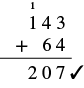 |
Nuestra respuesta es correcta.
Restar y luego verificar sumando:\(439 − 52\).
- Contestar
-
\(439-52=387\)porque\(387+52=439\)
Restar y luego verificar sumando:\(318 − 75\).
- Contestar
-
\(318-75=243\)porque\(243+75=318\)
Restar y luego verificar sumando:\(910 − 586\).
Solución
| Escribe los números para que cada valor posicional se alinee verticalmente. | 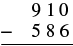 |
| Resta los unos. No podemos restar 6 de 0, así que tomamos prestado 1 diez y sumamos 10 a los 10 que teníamos. Esto hace 10 unos. Escribimos un 0 arriba del lugar de las decenas y tachamos el 1. Escribimos los 10 arriba del lugar unos y tachamos el 0. Ahora podemos restar los unos. 10 − 6 = 4. | 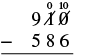 |
| Escribe el 4 en el lugar de la diferencia. | 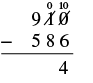 |
| Resta las decenas. No podemos restar 8 de 0, así que tomamos prestado cien y sumamos 10 decenas a las 0 decenas que teníamos, lo que nos da 10 decenas. Escribe 8 arriba del lugar de los cientos y tachar el 9. Escribe 10 arriba del lugar de las decenas. | 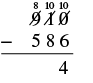 |
| Ahora podemos restar las decenas. 10 − 8 = 2. | 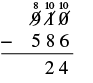 |
| Restar el lugar de los cientos. 8 − 5 = 3. Escribe el 3 en el lugar de los cientos en la diferencia. | 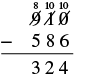 |
| Verifique agregando. |  |
Nuestra respuesta es correcta.
Restar y luego verificar sumando:\(832 − 376\).
- Contestar
-
\(832-376=456\)porque\(456+376=832\)
Restar y luego verificar sumando:\(847 − 578\).
- Contestar
-
\(847-578=269\)porque\(578+269=847\)
Restar y luego verificar sumando:\(2,162 − 479\).
Solución
| Escribe los números para que cada uno de los valores de lugar se alinee verticalmente. | 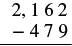 |
| Resta los unos. Ya que no podemos restar 9 de 2, pedir prestado 1 diez y sumar 10 unos a los 2 para hacer 12 unos. Escribe 5 arriba del lugar de las decenas y tachar el 6. Escribe 12 arriba del lugar unos y tachar el 2. | 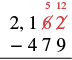 |
| Ahora podemos restar los unos. | 12 - 9 = 3 |
| Escribe 3 en el lugar de unos en la diferencia | 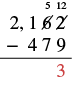 |
| Restar las decenas. Ya que no podemos restar 7 de 5, pedir prestado cien y sumar 10 decenas a las 5 decenas para hacer 15 decenas. Escribe 0 arriba del lugar de los cientos y tachar el 1. Escribe 15 arriba del lugar de las decenas. | 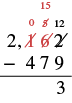 |
| Ahora podemos restar las decenas. | 15 - 7 = 8 |
| Escribe 8 en el lugar de las decenas en la diferencia. | 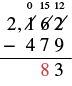 |
| Ahora podemos restar los cientos. | 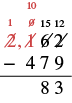 |
| Escribe 6 en el lugar de cientos en la diferencia | 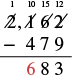 |
| Restar los miles. No hay dígito en el lugar de miles del número inferior, así que imaginamos un 0. 1 − 0 = 1. Escribe 1 en el lugar de miles de la diferencia. | 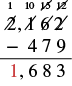 |
| Verifique agregando. | 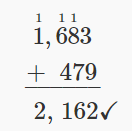 |
Nuestra respuesta es correcta.
Restar y luego verificar sumando:\(4,585 − 697\).
- Contestar
-
\(4,585-697=3,888\)porque\(3,888+697=4,585\)
Restar y luego verificar sumando:\(5,637 − 899\).
- Contestar
-
\(5,637-899=4,738\)porque\(4,738+899=5,637\)


