3.E: Enteros (Ejercicios)
- Page ID
- 114209
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)3.1 - Introducción a los números enteros
Localizar números positivos y negativos en la línea numérica
En los siguientes ejercicios, localice y etiquete el entero en la recta numérica.
- 5
- −5
- −3
- 3
- −8
- −7
Orden de números positivos y negativos
En los siguientes ejercicios, ordene cada uno de los siguientes pares de números, utilizando < or >.
- 4__8
- −6__3
- −5__−10
- −9__−4
- 2__−7
- −3__1
Encuentra opuestos
En los siguientes ejercicios, encuentra lo contrario de cada número.
- 6
- −2
- −4
- 3
En los siguientes ejercicios, simplifique.
- (a) − (8) (b) − (−8)
- (a) − (9) (b) − (−9)
En los siguientes ejercicios, evalúe.
- −x, cuando (a) x = 32 (b) x = −32
- −n, cuando (a) n = 20 (b) n = −20
Simplificar los valores absolutos
En los siguientes ejercicios, simplifique.
- |−21|
- |−42|
- |36|
- −|15|
- |0|
- −|−75|
En los siguientes ejercicios, evalúe.
- |x| cuando x = −14
- −|r| cuando r = 27
- −|−y| cuando y = 33
- |−n| cuando n = −4
En los siguientes ejercicios, rellene <, > o = para cada uno de los siguientes pares de números.
- −|−4|__4
- −2__|−2|
- −|−6|__−6
- −|−9|__|−9|
En los siguientes ejercicios, simplifique.
- − (−55) y − |−55|
- − (−48) y − |−48|
- |12 − 5|
- |9 + 7|
- 6|−9|
- |14−8| − |−2|
- |9 − 3| − |5 − 12|
- 5 + 4|15 − 3|
Traducir frases a expresiones con números enteros
En los siguientes ejercicios, traduzca cada una de las siguientes frases en expresiones con números positivos o negativos.
- lo contrario de 16
- lo contrario de −8
- negativo 3
- 19 menos menos 12
- una temperatura de 10 bajo cero
- una elevación de 85 pies bajo el nivel del mar
3.2 - Agregar números enteros
Adición de modelos de números enteros
En los siguientes ejercicios, modele lo siguiente para encontrar la suma.
- 3 + 7
- −2 + 6
- 5 + (−4)
- −3 + (−6)
Simplificar expresiones con números enteros
En los siguientes ejercicios, simplifique cada expresión.
- 14 + 82
- −33 + (−67)
- −75 + 25
- 54 + (−28)
- 11 + (−15) + 3
- −19 + (−42) + 12
- −3 + 6 (−1 + 5)
- 10 + 4 (−3 + 7)
Evaluar expresiones variables con números enteros
En los siguientes ejercicios, evalúe cada expresión.
- n + 4 cuando (a) n = −1 (b) n = −20
- x + (−9) cuando (a) x = 3 (b) x = −3
- (x + y) 3 cuando x = −4, y = 1
- (u + v) 2 cuando u = −4, v = 11
Traducir frases de palabras a expresiones algebraicas
En los siguientes ejercicios, traducir cada frase en una expresión algebraica y luego simplificar.
- la suma de −8 y 2
- 4 más de −12
- 10 más que la suma de −5 y −6
- la suma de 3 y −5, incrementada en 18
Agregar números enteros en aplicaciones
En los siguientes ejercicios, resuelve.
- Temperatura El lunes, la temperatura alta en Denver fue de −4 grados. La temperatura alta del martes fue de 20 grados más. ¿Cuál fue la alta temperatura del martes?
- Crédito Frida adeudaba 75 dólares en su tarjeta de crédito. Después cobró 21 dólares más. ¿Cuál era su nuevo saldo?
3.3 - Restar enteros
Modelo de resta de números enteros
En los siguientes ejercicios, modele lo siguiente.
- 6 − 1
- −4 − (−3)
- 2 − (−5)
- −1 − 4
Simplificar expresiones con números enteros
En los siguientes ejercicios, simplifique cada expresión.
- 24 − 16
- 19 − (−9)
- −31 − 7
- −40 − (−11)
- −52 − (−17) − 23
- 25 − (−3 − 9)
- (1 − 7) − (3 − 8)
- 3 2 − 7 2
Evaluar expresiones variables con números enteros
En los siguientes ejercicios, evalúe cada expresión.
- x − 7 cuando (a) x = 5 (b) x = −4
- 10 − y cuando (a) y = 15 (b) y = −16
- 2n 2 − n + 5 cuando n = −4
- −15 − 3u 2 cuando u = −5
Traducir frases a expresiones algebraicas
En los siguientes ejercicios, traducir cada frase en una expresión algebraica y luego simplificar.
- la diferencia de −12 y 5
- restar 23 de −50
Restar enteros en aplicaciones
En los siguientes ejercicios, resolver las aplicaciones dadas.
- Temperatura Una mañana la temperatura en Bangor, Maine era de 18 grados. Por la tarde, había bajado 20 grados. ¿Cuál era la temperatura de la tarde?
- Temperatura El 4 de enero, la temperatura alta en Laredo, Texas, fue de 78 grados, y la alta en Houlton, Maine, fue de −28 grados. ¿Cuál fue la diferencia de temperatura de Laredo y Houlton?
3.4 - Multiplicar y dividir enteros
Multiplicar enteros
En los siguientes ejercicios, multiplicar.
- −9 • 4
- 5 (−7)
- (−11) (−11)
- −1 • 6
Dividir enteros
En los siguientes ejercicios, divide.
- 56 ÷ (−8)
- −120 ÷ (−6)
- −96 ÷ 12
- 96 ÷ (−16)
- 45 ÷ (−1)
- −162 ÷ (−1)
Simplificar expresiones con números enteros
En los siguientes ejercicios, simplifique cada expresión.
- 5 (−9) − 3 (−12)
- (−2) 5
- −3 4
- (−3) (4) (−5) (−6)
- 42 − 4 (6 − 9)
- (8 − 15) (9 − 3)
- −2 (−18) ÷ 9
- 45 ÷ (−3) − 12
Evaluar expresiones variables con números enteros
En los siguientes ejercicios, evalúe cada expresión.
- 7x − 3 cuando x = −9
- 16 − 2n cuando n = −8
- 5a + 8b cuando a = −2, b = −6
- x 2 + 5x + 4 cuando x = −3
Traducir frases de palabras a expresiones algebraicas
En los siguientes ejercicios, traduzca a una expresión algebraica y simplifique si es posible.
- el producto de −12 y 6
- el cociente de 3 y la suma de −7 y s
3.5 - Resolver ecuaciones usando números enteros; La propiedad de división de igualdad
Determinar si un número es una solución de una ecuación
En los siguientes ejercicios, determinar si cada número es una solución de la ecuación dada.
- 5x − 10 = −35
- x = −9
- x = −5
- x = 5
- 8u + 24 = −32
- u = −7
- u = −1
- u = 7
Uso de las Propiedades de Suma y Resta de Igualdad
En los siguientes ejercicios, resuelve.
- a + 14 = 2
- b − 9 = −15
- c + (−10) = −17
- d − (−6) = −26
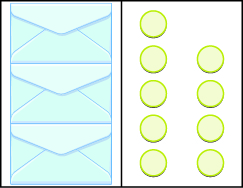
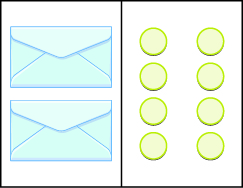
Modelar la División Propiedad de Igualdad
En los siguientes ejercicios, escribe la ecuación modelada por los sobres y contadores. Entonces resolverlo.
Resolver ecuaciones usando la propiedad de división de igualdad
En los siguientes ejercicios, resuelve cada ecuación usando la propiedad de división de igualdad y verifica la solución.
- 8p = 72
- −12q = 48
- −16r = −64
- −5s = −100
Traducir a una Ecuación y Resolver.
En los siguientes ejercicios, traduzca y resuelva.
- El producto de −6 e y es −42
- La diferencia de z y −13 es −18.
- Cuatro más de m es −48.
- El producto de −21 y n es 63.
Matemáticas cotidianas
- Describe cómo has usado dos temas de este capítulo en tu vida fuera de tu clase de matemáticas durante el mes pasado.
PRUEBA DE PRÁCTICA
- Localice y etiquete 0, 2, −4 y −1 en una recta numérica.
En los siguientes ejercicios, compare los números, usando < or > o =.
- (a) −6__3 (b) −1__−4
- (a) −5__|−5| (b) −|−2|__−2
En los siguientes ejercicios, encuentra lo contrario de cada número.
- (a) −7 (b) 8
En los siguientes ejercicios, simplifique.
- − (−22)
- |4 − 9|
- −8 + 6
- −15 + (−12)
- −7 − (−3)
- 10 − (5 − 6)
- −3 • 8
- −6 (−9)
- 70 ÷ (−7)
- (−2) 3
- −4 2
- 16−3 (5−7)
- |21 − 6| − |−8|
En los siguientes ejercicios, evalúe.
- 35 − a cuando a = −4
- (−2r) 2 cuando r = 3
- 3m − 2n cuando m = 6, n = −8
- −|−y| cuando y = 17
En los siguientes ejercicios, traducir cada frase en una expresión algebraica y luego simplificar, si es posible.
- la diferencia de −7 y −4
- el cociente de 25 y la suma de m y n.
En los siguientes ejercicios, resuelve.
- Temprano una mañana, la temperatura en Siracusa era de −8°F. Al mediodía, había subido 12°. ¿Cuál era la temperatura al mediodía?
- Collette debía 128 dólares en su tarjeta de crédito. Después cobró 65 dólares. ¿Cuál era su nuevo saldo?
En los siguientes ejercicios, resuelve.
- n + 6 = 5
- p − 11 = −4
- −9r = −54
En los siguientes ejercicios, traduzca y resuelva.
- El producto de 15 y x es 75.
- Ocho menos que y es −32.