Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

4.E: Fracciones (Ejercicios)

Última actualización

30 oct 2022
Guardar como PDF
- 4.9: Suma y resta fracciones con diferentes denominadores (Parte 2)
- 4.S: Fracciones (Resumen)

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

4.1 - Visualizar fracciones

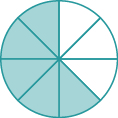
En los siguientes ejercicios, nombra la fracción de cada figura que esté sombreada.

$Se muestra un círculo. Se divide en 8 piezas iguales. 5 piezas están sombreadas.$
$Se muestra un cuadrado. Se divide en 9 piezas iguales. 5 piezas están sombreadas.$

En los siguientes ejercicios, nombra las fracciones impropias. Después escribe cada fracción impropia como un número mixto.

$Se muestran dos cuadrados. Ambos se dividen en cuatro piezas iguales. El cuadrado de la izquierda tiene las 4 piezas sombreadas. El cuadrado de la derecha tiene una pieza sombreada.$
$Se muestran dos círculos. Ambos se dividen en dos piezas iguales. El círculo de la izquierda tiene ambas piezas sombreadas. El círculo de la derecha tiene una pieza sombreada.$

En los siguientes ejercicios, convertir la fracción impropia a un número mixto.

$\dfrac{58}{15}$
$\dfrac{63}{11}$

En los siguientes ejercicios, convertir el número mixto a una fracción impropia.

$12 \dfrac{1}{4}$
$9 \dfrac{4}{5}$
Encuentra tres fracciones equivalentes a $\dfrac{2}{5}$ . Muestra tu obra, usando figuras o álgebra.
Encuentra tres fracciones equivalentes a $− \dfrac{4}{3}$ . Muestra tu obra, usando figuras o álgebra.

En los siguientes ejercicios, ubique los números en una recta numérica.

$\dfrac{5}{8}, \dfrac{4}{3}, 3 \dfrac{3}{4}$ , 4
$\dfrac{1}{4}, − \dfrac{1}{4}, 1 \dfrac{1}{3}, −1 \dfrac{1}{3}, \dfrac{7}{2}, − \dfrac{7}{2}$

En los siguientes ejercicios, ordene cada par de números, utilizando < or >.

−1___ $− \dfrac{2}{5}$
$−2 \dfrac{1}{2}$ ___−3

4.2 - Multiplicar y dividir fracciones

En los siguientes ejercicios, simplifique.

$− \dfrac{63}{84}$
$− \dfrac{90}{120}$
$− \dfrac{14a}{14b}$
$− \dfrac{8x}{8y}$

En los siguientes ejercicios, multiplicar.

$\dfrac{2}{5} \cdot \dfrac{8}{13}$
$− \dfrac{1}{3} \cdot \dfrac{12}{7}$
$\dfrac{2}{9} \cdot \left(− \dfrac{45}{32}\right)$
6m $\cdot \dfrac{4}{11}$
$− \dfrac{1}{4}$ (−32)
$3 \dfrac{1}{5} \cdot 1 \dfrac{7}{8}$

En los siguientes ejercicios, encuentra el recíproco.

$\dfrac{2}{9}$
$\dfrac{15}{4}$
3
$− \dfrac{1}{4}$
Rellene la tabla.

	Opuesto	Valor Absoluto	recíproco
$- \dfrac{5}{13}$
$\dfrac{3}{10}$
$\dfrac{9}{4}$
-12

En los siguientes ejercicios, divide.

$\dfrac{2}{3} \div \dfrac{1}{6}$
$\left(− \dfrac{3x}{5}\right) \div \left(− \dfrac{2y}{3}\right)$
$\dfrac{4}{5} \div$ 3
8 $\div 2 \dfrac{2}{3}$
$8 \dfrac{2}{3} \div 1 \dfrac{1}{12}$

4.3 - Multiplicar y dividir números mixtos y fracciones complejas

En los siguientes ejercicios, realice la operación indicada.

$3 \dfrac{1}{5} \cdot 1 \dfrac{7}{8}$
$−5 \dfrac{7}{12} \cdot 4 \dfrac{4}{11}$
8 $\div 2 \dfrac{2}{3}$
$8 \dfrac{2}{3} \div 1 \dfrac{1}{12}$

En los siguientes ejercicios, traducir la frase en inglés a una expresión algebraica.

el cociente de 8 e y
el cociente de V y la diferencia de h y 6

En los siguientes ejercicios, simplificar la fracción compleja.

$\dfrac{\dfrac{5}{8}}{\dfrac{4}{5}}$
$\dfrac{\dfrac{8}{9}}{−4}$
$\dfrac{\dfrac{n}{4}}{\dfrac{3}{8}}$
$\dfrac{−1 \dfrac{5}{6}}{− \dfrac{1}{12}}$

En los siguientes ejercicios, simplifique.

$\dfrac{5 + 16}{5}$
$\dfrac{8 \cdot 4 − 5^{2}}{3 \cdot 12}$
$\dfrac{8 \cdot 7 + 5(8 − 10)}{9 \cdot 3 − 6 \cdot 4}$

4.4 - Suma y resta fracciones con denominadores comunes

En los siguientes ejercicios, agregue.

$\dfrac{3}{8} + \dfrac{2}{8}$
$\dfrac{4}{5} + \dfrac{1}{5}$
$\dfrac{2}{5} + \dfrac{1}{5}$
$\dfrac{15}{32} + \dfrac{9}{32}$
$\dfrac{x}{10} + \dfrac{7}{10}$

En los siguientes ejercicios, restar.

$\dfrac{8}{11} − \dfrac{6}{11}$
$\dfrac{11}{12} − \dfrac{5}{12}$
$\dfrac{4}{5} − \dfrac{y}{5}$
$− \dfrac{31}{30} − \dfrac{7}{30}$
$\dfrac{3}{2} − \left(\dfrac{3}{2}\right)$
$\dfrac{11}{15} − \dfrac{5}{15} − \left(− \dfrac{2}{15}\right)$

4.5 - Suma y resta fracciones con diferentes denominadores

En los siguientes ejercicios, encuentra el mínimo denominador común.

$\dfrac{1}{3}$ y $\dfrac{1}{12}$
$\dfrac{1}{3}$ y $\dfrac{4}{5}$
$\dfrac{8}{15}$ y $\dfrac{11}{20}$
$\dfrac{3}{4}, \dfrac{1}{6}$ , y $\dfrac{5}{10}$

En los siguientes ejercicios, cambie a fracciones equivalentes usando el LCD dado.

$\dfrac{1}{3}$ y $\dfrac{1}{5}$ , LCD = 15
$\dfrac{3}{8}$ y $\dfrac{5}{6}$ , LCD = 24
$− \dfrac{9}{16}$ y $\dfrac{5}{12}$ , LCD = 48
$\dfrac{1}{3}, \dfrac{3}{4}$ y $\dfrac{4}{5}$ , LCD = 60

En los siguientes ejercicios, realizar las operaciones indicadas y simplificar.

$\dfrac{1}{5} + \dfrac{2}{3}$
$\dfrac{11}{12} − \dfrac{2}{3}$
$− \dfrac{9}{10} − \dfrac{3}{4}$
$− \dfrac{11}{36} − \dfrac{11}{20}$
$− \dfrac{22}{25} + \dfrac{9}{40}$
$\dfrac{y}{10} − \dfrac{1}{3}$
$\dfrac{2}{5} + \left(− \dfrac{5}{9}\right)$
$\dfrac{4}{11} \div \dfrac{2}{7d}$
$\dfrac{2}{5} + \left(− \dfrac{3n}{8}\right) \left(− \dfrac{2}{9n}\right)$
$\dfrac{\left(\dfrac{2}{3}\right)^{2}}{\left(\dfrac{5}{8}\right)^{2}}$
$\left(\dfrac{11}{12} + \dfrac{3}{8}\right) \div \left(\dfrac{5}{6} − \dfrac{1}{10}\right)$

En los siguientes ejercicios, evalúe.

y − $\dfrac{4}{5}$ cuando (a) y = $− \dfrac{4}{5}$ (b) y = $\dfrac{1}{4}$
6mn ² cuando m = $\dfrac{3}{4}$ y n = $− \dfrac{1}{3}$

4.6 - Suma y resta números mixtos

En los siguientes ejercicios, realice la operación indicada.

$4 \dfrac{1}{3} + 9 \dfrac{1}{3}$
$6 \dfrac{2}{5} + 7 \dfrac{3}{5}$
$5 \dfrac{8}{11} + 2 \dfrac{4}{11}$
$3 \dfrac{5}{8} + 3 \dfrac{7}{8}$
$9 \dfrac{13}{20} − 4 \dfrac{11}{20}$
$2 \dfrac{3}{10} − 1 \dfrac{9}{10}$
$2 \dfrac{11}{12} − 1 \dfrac{7}{12}$
$8 \dfrac{6}{11} − 2 \dfrac{9}{11}$

4.7 - Resolver ecuaciones con fracciones

En los siguientes ejercicios, determinar si cada número es una solución de la ecuación dada.

x − $\dfrac{1}{2}$ = $\dfrac{1}{6}$ :
1. x = 1
2. x = $\dfrac{2}{3}$
3. x = $− \dfrac{1}{3}$
y + $\dfrac{3}{5}$ = $\dfrac{5}{9}$ :
1. y = $\dfrac{1}{2}$
2. y = $\dfrac{52}{45}$
3. y = $− \dfrac{2}{45}$

En los siguientes ejercicios, resuelve la ecuación.

n + $\dfrac{9}{11}$ = $\dfrac{4}{11}$
x − $\dfrac{1}{6}$ = $\dfrac{7}{6}$
h − $\left(- \dfrac{7}{8}\right)$ = $− \dfrac{2}{5}$
$\dfrac{x}{5}$ = −10
−z = 23

En los siguientes ejercicios, traduzca y resuelva.

La suma de dos tercios y n es $− \dfrac{3}{5}$ .
La diferencia de q y una décima es $\dfrac{1}{2}$ .
El cociente de p y −4 es −8.
Tres octavos de y es 24.

PRUEBA DE PRÁCTICA

Convertir la fracción impropia a un número mixto.

$\dfrac{19}{5}$

Convertir el número mixto en una fracción impropia.

$3 \dfrac{2}{7}$

Localice los números en una recta numérica.

$\dfrac{1}{2}, 1 \dfrac{2}{3}, −2 \dfrac{3}{4}$ , y $\dfrac{9}{4}$

En los siguientes ejercicios, simplifique.

$\dfrac{5}{20}$
$\dfrac{18r}{27s}$
$\dfrac{1}{3} \cdot \dfrac{3}{4}$
$\dfrac{3}{5} \cdot$ 15
−36u $\left(− \dfrac{4}{9}\right)$
$−5 \dfrac{7}{12} \cdot 4 \dfrac{4}{11}$
$− \dfrac{5}{6} \div \dfrac{5}{12}$
$\dfrac{7}{11} \div \left(− \dfrac{7}{11}\right)$
$\dfrac{9a}{10} \div \dfrac{15a}{8}$
$−6 \dfrac{2}{5} \div$ 4
$\left(−15 \dfrac{5}{6}\right) \div \left(−3 \dfrac{1}{6}\right)$
$\dfrac{−6}{\dfrac{6}{11}}$
$\dfrac{\dfrac{p}{2}}{\dfrac{q}{5}}$
$\dfrac{− \dfrac{4}{15}}{−2 \dfrac{2}{3}}$
$\dfrac{9^{2} − 4^{2}}{9 − 4}$
$\dfrac{2}{d} + \dfrac{9}{d}$
$− \dfrac{3}{13} + \left(− \dfrac{4}{13}\right)$
$− \dfrac{22}{25} + \dfrac{9}{40}$
$\dfrac{2}{5} + \left(− \dfrac{7}{5}\right)$
$− \dfrac{3}{10} + \left(- \dfrac{5}{8}\right)$
$− \dfrac{3}{4} \div \dfrac{x}{3}$
$\dfrac{2^{3} − 2^{2}}{\left(\dfrac{3}{4}\right)^{2}}$
$\dfrac{\dfrac{5}{14} + \dfrac{1}{8}}{\dfrac{9}{56}}$

Evaluar.

x + $\dfrac{1}{3}$ cuando (a) x = $\dfrac{2}{3}$ (b) x = $− \dfrac{5}{6}$

En los siguientes ejercicios, resuelve la ecuación.

y + $\dfrac{3}{5}$ = $\dfrac{7}{5}$
a − $\dfrac{3}{10}$ = $− \dfrac{9}{10}$
f + $\left(− \dfrac{2}{3}\right)$ = $\dfrac{5}{12}$
$\dfrac{m}{−2}$ = −16
$− \dfrac{2}{3}$ c = 18
Traducir y resolver: El cociente de p y −4 es −8. Resolver para p.

Colaboradores y Atribuciones

Template:ContribOpenStaxPreAlgebra

4.1 - Visualizar fracciones

4.2 - Multiplicar y dividir fracciones

4.3 - Multiplicar y dividir números mixtos y fracciones complejas

4.4 - Suma y resta fracciones con denominadores comunes

4.5 - Suma y resta fracciones con diferentes denominadores

4.6 - Suma y resta números mixtos

4.7 - Resolver ecuaciones con fracciones

PRUEBA DE PRÁCTICA

Colaboradores y Atribuciones

Support Center

How can we help?