7.5: Hipérbolas
- Page ID
- 119462
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)En la definición de elipse, Definición 7.4, fijamos dos puntos llamados focos y miramos puntos cuyas distancias a los focos siempre se sumaban a una distancia constante\(d\). Aquellos propensos a retoques sintácticos pueden preguntarse qué curva, si la hubiera, generaríamos si reemplazáramos sumado por restado. La respuesta es una hipérbola.
Dados dos puntos distintos\(F_{1}\) y\(F_{2}\) en el plano y una distancia fija\(d\), una hipérbola es el conjunto de todos los puntos\((x, y)\) en el plano tal que el valor absoluto de la diferencia de cada una de las distancias desde\(F_{1}\) y\(F_{2}\) hacia\((x, y)\) es\(d\). Los puntos\(F_{1}\) y\(F_{2}\) se llaman los focos de la hipérbola.
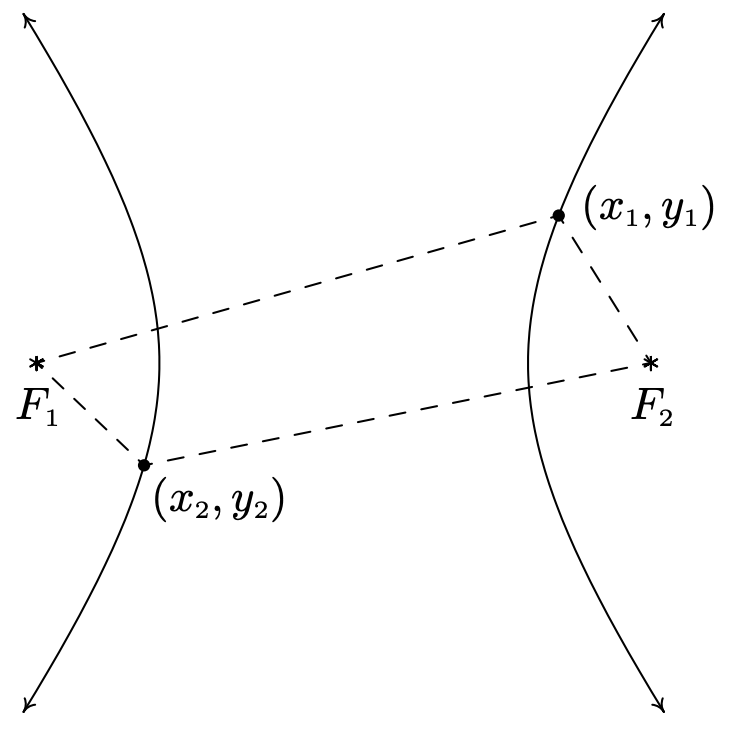
En la figura anterior:
\[\begin{array}{rclr} \mbox{the distance from $F_1$ to $(x_1, y_1)$} - \mbox{the distance from $F_2$ to $(x_1, y_1)$} & = & d & \\ \end{array}\nonumber\]
y
\[\begin{array}{rclr} \mbox{the distance from $F_2$ to $(x_2, y_2)$} - \mbox{the distance from $F_1$ to $(x_2, y_2)$} & = & d & \\ \end{array}\nonumber\]
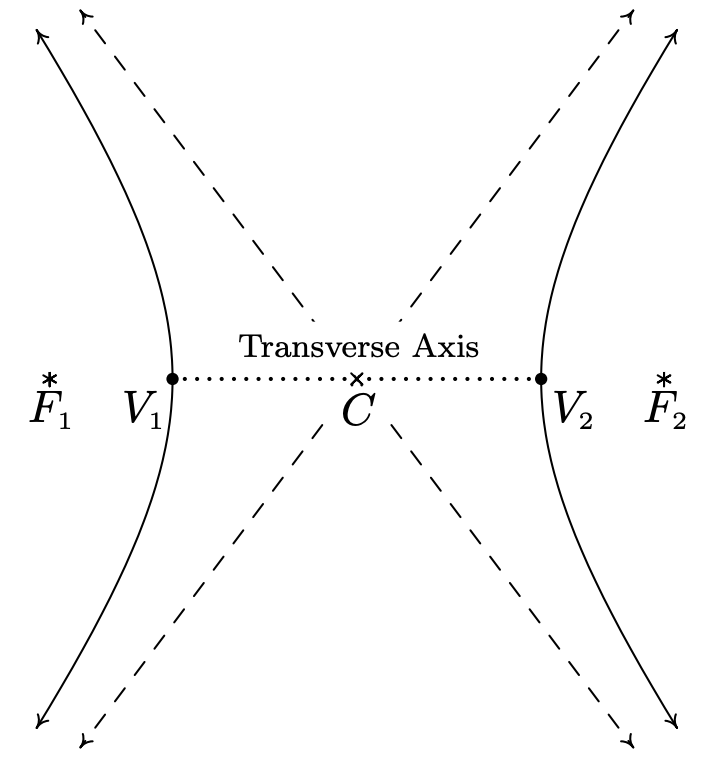
Tenga en cuenta que la hipérbola tiene dos partes, llamadas ramas. El centro de la hipérbola es el punto medio del segmento lineal que conecta los dos focos. El eje transversal de la hipérbola es el segmento lineal que conecta dos extremos opuestos de la hipérbola que también contiene el centro y los focos. Los vértices de una hipérbola son los puntos de la hipérbola que se encuentran en el eje transversal. Además, mostraremos momentáneamente que existen líneas llamadas asíntotas a las que se acercan las ramas de la hipérbola para grandes\(x\) y\(y\) valores. Sirven como guías para la gráfica. En imágenes,
Antes de derivar la ecuación estándar de la hipérbola, necesitamos discutir otro parámetro, el eje conjugado de la hipérbola. El eje conjugado de una hipérbola es el segmento lineal a través del centro que es perpendicular al eje transversal y tiene la misma longitud que el segmento lineal a través de un vértice que conecta las asíntotas. En fotos tenemos
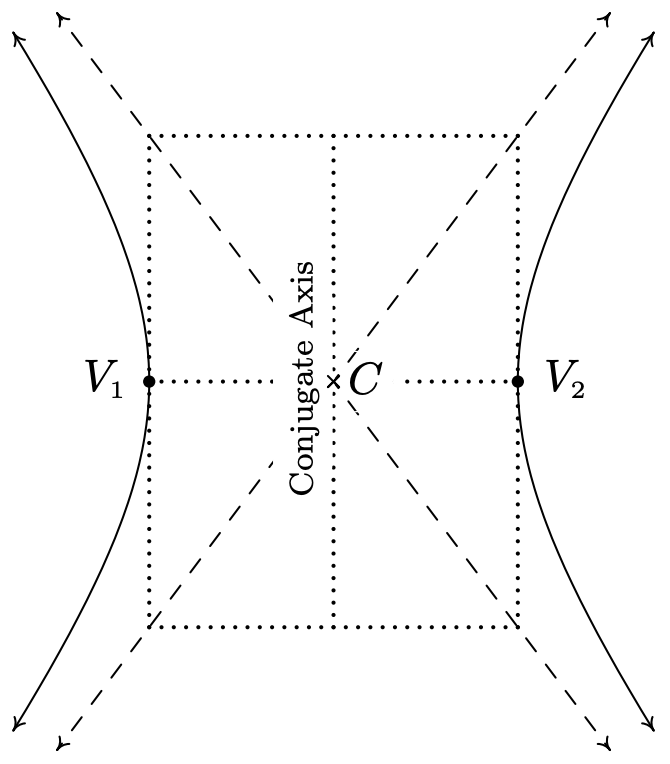
Obsérvese que en el diagrama, podemos construir un rectángulo utilizando segmentos de línea con longitudes iguales a las longitudes de los ejes transversal y conjugado cuyo centro es el centro de la hipérbola y cuyas diagonales están contenidas en las asíntotas. Este rectángulo guía, muy parecido al que vimos Sección 7.4 para ayudarnos a graficar elipses, nos ayudará a graficar hipérbolas.
Supongamos que deseamos derivar la ecuación de una hipérbola. Por simplicidad, asumiremos que el centro es\((0,0)\), los vértices son\((a,0)\) y\((-a,0)\) y los focos son\((c,0)\) y\((-c,0)\). Etiquetamos los puntos finales del eje conjugado\((0,b)\) y\((0,-b)\). (Aunque\(b\) no entra en nuestra derivación, tendremos que justificar esta elección como verá más adelante.) Como antes, suponemos\(a\),\(b\), y\(c\) son todos números positivos. Esquemáticamente tenemos
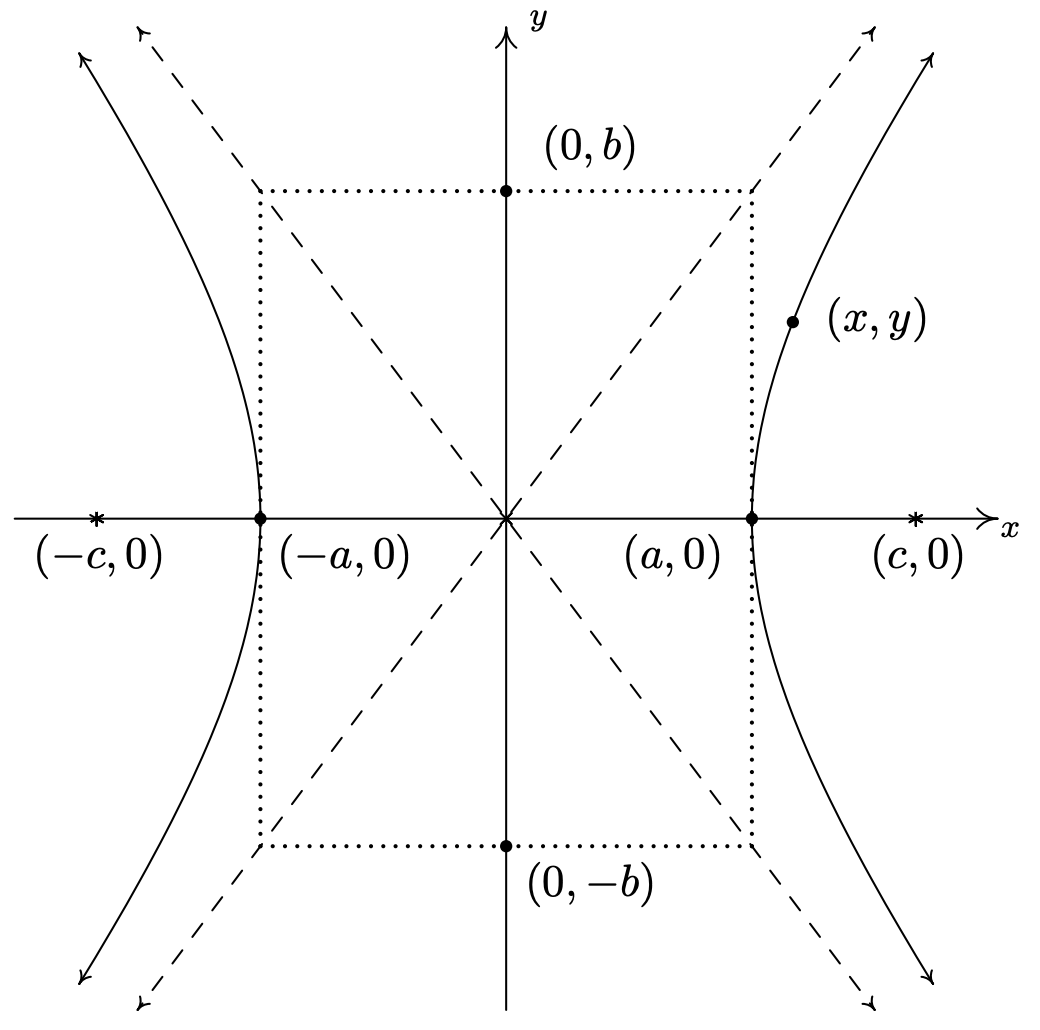
Ya que\((a,0)\) está en la hipérbola, debe cumplir las condiciones de la Definición 7.6. Es decir, la distancia de\((-c,0)\) a\((a,0)\) menos la distancia de\((c,0)\) a\((a,0)\) debe ser igual a la distancia fija\(d\). Dado que todos estos puntos se encuentran en el\(x\) eje, obtenemos
\[\begin{array}{rclr} \mbox{distance from $(-c,0)$ to $(a,0)$} - \mbox{distance from $(c,0)$ to $(a,0)$} & = & d & \\ (a+c) - (c-a) & = & d & \\ 2a & = & d \\ \end{array}\nonumber\]
En otras palabras, ¡la distancia fija\(d\) desde la definición de la hipérbola es en realidad la longitud del eje transversal! (¿Dónde hemos visto antes ese tipo de coincidencia?) Consideremos ahora un punto\((x,y)\) sobre la hipérbola. Aplicando la Definición 7.6, obtenemos
\[\begin{array}{rclr} \mbox{distance from $(-c,0)$ to $(x,y)$} - \mbox{distance from $(c,0)$ to $(x,y)$} & = & 2a & \\ \sqrt{(x-(-c))^2+(y-0)^2} - \sqrt{(x-c)^2+(y-0)^2} & = & 2a & \\ \sqrt{(x+c)^2+y^2} - \sqrt{(x-c)^2+y^2} & = & 2a \\ \end{array}\nonumber\]
Usando el mismo arsenal de armamento de Álgebra Intermedia que usamos para derivar la fórmula estándar de una elipse, Ecuación 7.4, llegamos a lo siguiente. 1
\[\begin{array}{rclr} \left(a^2 - c^2\right) x^2 +a^2 y^2 & = & a^2 \left(a^2 - c^2\right) & \end{array}\nonumber\]
Lo que queda es determinar la relación entre\(a\),\(b\) y\(c\). Para ello, observamos que desde\(a\) y\(c\) son ambos números positivos con\(a < c\), obtenemos\(a^2 < c^2\) así que ese\(a^2 - c^2\) es un número negativo. De ahí,\(c^2 - a^2\) es un número positivo. Por razones que pronto quedarán claras, reescribimos la ecuación resolviendo\(y^2/x^2\) para obtener
\[\begin{array}{rclr} \left(a^2 - c^2\right) x^2 +a^2 y^2 & = & a^2 \left(a^2 - c^2\right) & \\ -\left(c^2 - a^2\right) x^2 +a^2 y^2 & = & -a^2 \left(c^2 - a^2\right) & \\ a^2 y^2 & = & \left(c^2 - a^2\right) x^2 - a^2\left(c^2 - a^2\right)& \\ \dfrac{y^2}{x^2} & = & \dfrac{\left(c^2 - a^2\right)}{a^2} - \dfrac{\left(c^2 - a^2\right)}{x^2}& \\ \end{array}\nonumber\]
Como\(x\) y\(y\) alcanzar valores muy grandes, la cantidad\(\frac{\left(c^2 - a^2\right)}{x^2} \rightarrow 0\) para que\(\frac{y^2}{x^2} \rightarrow \frac{\left(c^2 - a^2\right)}{a^2}\). Al establecer\(b^{2} = c^{2} - a^{2}\) obtenemos\(\frac{y^2}{x^2} \rightarrow \frac{b^2}{a^2}\). Esto demuestra que a\(y \rightarrow \pm \frac{b}{a} x\) medida que\(|x|\) crece grande. Así\(y = \pm \frac{b}{a} x\) son las asíntotas a la gráfica como se predijo y se justifica nuestra elección de etiquetas para los puntos finales del eje conjugado. En nuestra ecuación de la hipérbola podemos sustituir\(a^2 - c^2 = -b^2\) qué rendimientos
\[\begin{array}{rclr} \left(a^2 - c^2\right) x^2 +a^2 y^2 & = & a^2 \left(a^2 - c^2\right) &\\ -b^2 x^2 +a^2 y^2 & = & - a^2 b^2 & \\ \dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} & = & 1 & \end{array}\nonumber\]
La ecuación anterior es para una hipérbola cuyo centro es el origen y que se abre a la izquierda y a la derecha. Si la hipérbola estuviera centrada en un punto\((h,k)\), obtendríamos lo siguiente.
La Ecuación Estándar de una Hipérbola Horizontal Para números positivos\(a\) y\(b\), la ecuación de una hipérbola horizontal con centro\((h,k)\) es
\[\dfrac{(x-h)^2}{a^2} - \dfrac{(y-k)^2}{b^2} = 1\nonumber\]
a Es decir, una hipérbola cuyas ramas se abren a la izquierda y a la derecha
Si los papeles de\(x\) y\(y\) se intercambiaran, entonces las ramas de la hipérbola se abrirían hacia arriba y hacia abajo y obtendríamos una hipérbola 'vertical'.
La ecuación estándar de una hipérbola vertical Para números positivos\(a\) y\(b\), la ecuación de una hipérbola vertical con centro\((h,k)\) es:
\[\dfrac{(y-k)^2}{b^2} - \dfrac{(x-h)^2}{a^2} = 1\nonumber\]
Los valores de\(a\) y\(b\) determinan qué tan lejos en las\(y\) direcciones\(x\) y, respectivamente, se cuenta desde el centro para determinar el rectángulo a través del cual pasan las asíntotas. En ambos casos, la distancia desde el centro a los focos\(c\), como se ve en la derivación, se puede encontrar por la fórmula\(c = \sqrt{a^2 + b^2}\). Por último, tenga en cuenta que podemos distinguir rápidamente la ecuación de una hipérbola de la de un círculo o elipse porque la fórmula de la hipérbola implica una diferencia de cuadrados donde las fórmulas círculo y elipse involucran la suma de cuadrados.
Grafica la ecuación\(\frac{(x-2)^2}{4} -\frac{y^2}{25} = 1.\) Encuentra el centro, las líneas que contienen los ejes transversal y conjugado, los vértices, los focos y las ecuaciones de las asíntotas.
Solución
Primero vemos que esta ecuación se nos da en la forma estándar de la Ecuación 7.6. Aquí\(x-h\) es\(x-2\) así\(h = 2\), y\(y-k\) es\(y\) así\(k = 0\). De ahí que nuestra hipérbola se centre en\((2,0)\). Vemos eso\(a^2 = 4\) así\(a = 2\), y\(b^2 = 25\) así\(b=5\). Esto significa que movemos\(2\) unidades a la izquierda y derecha del centro y\(5\) unidades arriba y abajo desde el centro para llegar a puntos en el rectángulo guía. Las asíntotas pasan por el centro de la hipérbola así como las esquinas del rectángulo. Esto arroja la siguiente puesta en marcha.
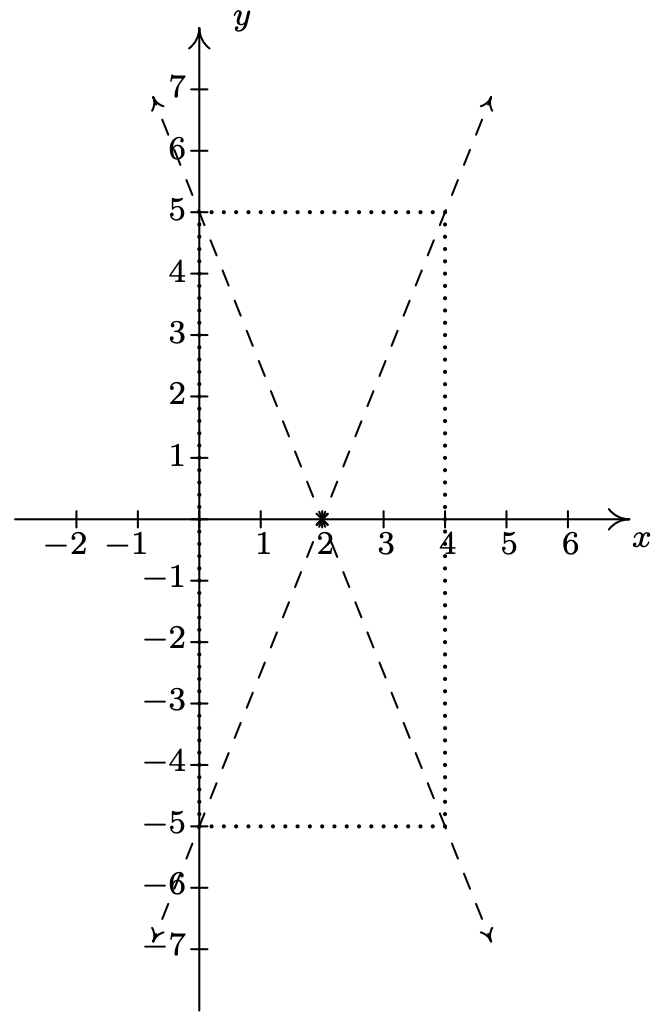
Ya que el\(y^2\) término se está restando del\(x^2\) término, sabemos que las ramas de la hipérbola se abren a izquierda y derecha. Esto significa que el eje transversal se encuentra a lo largo del\(x\) eje. De ahí que el eje conjugado se encuentre a lo largo de la línea vertical\(x = 2\). Dado que los vértices de la hipérbola son donde la hipérbola se cruza con el eje transversal, obtenemos que los vértices son\(2\) unidades a la izquierda y derecha de\((2,0)\) at\((0,0)\) y\((4,0)\). Para encontrar los focos, necesitamos\(c = \sqrt{a^2 + b^2} = \sqrt{4+25} = \sqrt{29}\). Dado que los focos se encuentran en el eje transversal, movemos\(\sqrt{29}\) las unidades a la izquierda y derecha de\((2,0)\) para llegar a\((2 - \sqrt{29},0)\) (aproximadamente\((-3.39, 0)\)) y\((2 + \sqrt{29}, 0)\) (aproximadamente\((7.39, 0)\)). Para determinar las ecuaciones de las asíntotas, recordemos que las asíntotas pasan por el centro de la hipérbola\((2,0)\), así como las esquinas del rectángulo guía, por lo que tienen pendientes de\(\pm \frac{b}{a} = \pm \frac{5}{2}\). Usando la ecuación punto-pendiente de una línea, Ecuación 2.2\(y -0 = \pm \frac{5}{2} (x - 2)\), rinde, así obtenemos\(y = \frac{5}{2}x - 5\) y\(y = -\frac{5}{2}x + 5\). Poniéndolo todo junto, obtenemos
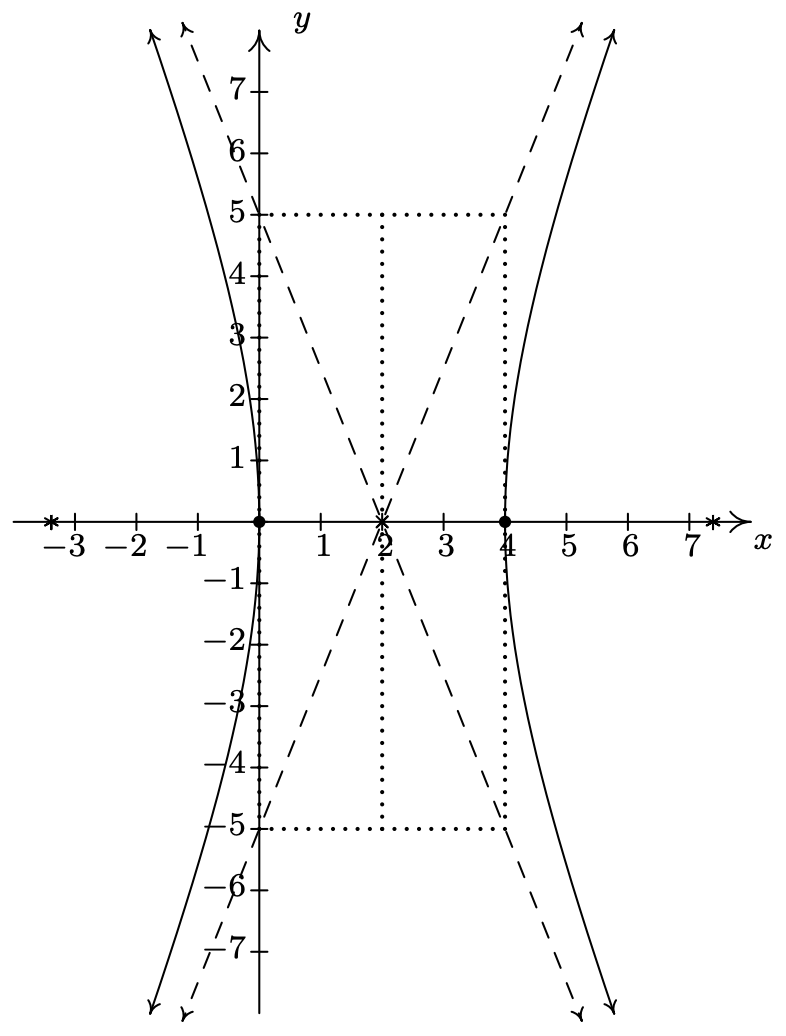
Encuentra la ecuación de la hipérbola con asíntotas\(y= \pm 2x\) y vértices\((\pm 5,0)\).
Solución
Trazar los datos que nos han dado, tenemos
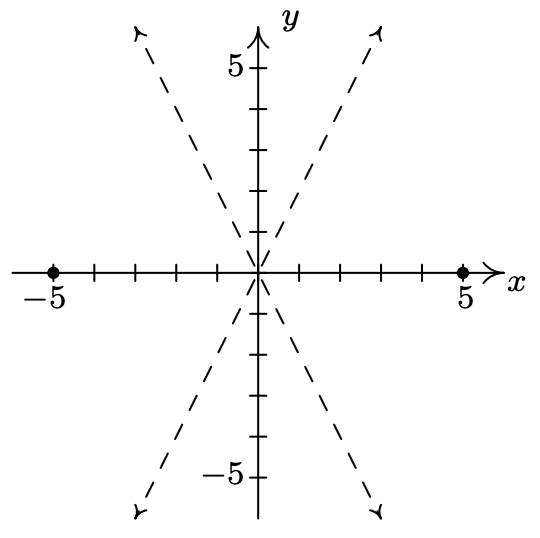
Esta gráfica no sólo nos dice que las ramas de la hipérbola se abren a la izquierda y a la derecha, también nos dice que el centro es\((0,0)\). De ahí que nuestra forma estándar sea\(\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1\). Ya que los vértices son\((\pm 5, 0)\),\(a=5\) así lo tenemos\(a^2 = 25\). Para determinar\(b^2\), recordamos que las laderas de las asíntotas son\(\pm \frac{b}{a}\). Ya que\(a = 5\) y la pendiente de la línea\(y=2x\) es\(2\), tenemos eso\(\frac{b}{5} = 2\), así\(b=10\). De ahí,\(b^2 = 100\) y nuestra respuesta final es\(\frac{x^2}{25} - \frac{y^2}{100} = 1\).
Al igual que con las otras secciones cónicas, una ecuación cuya gráfica es una hipérbola puede no darse en ninguna de las formas estándar. Para rectificar eso, tenemos lo siguiente.
Escribir la ecuación de una hipérbola en forma estándar
- Agrupar las mismas variables en un lado de la ecuación y posicionar la constante en el otro lado
- Completar el cuadrado en ambas variables según sea necesario
- Divide ambos lados por el término constante para que la constante en el otro lado de la ecuación se convierta\(1\)
Considera la ecuación\(9y^2-x^2-6x=10\). Poner esta ecuación en forma estándar y graficar. Encuentra el centro, las líneas que contienen los ejes transversales y conjugados, los vértices, los focos y las ecuaciones de las asíntotas.
Solución
Solo necesitamos completar el cuadrado en\(x\):
\[\begin{array}{rclr} 9y^2-x^2-6x & = & 10 & \\[5pt] 9y^2-1\left(x^2+6x\right) & = & 10 & \\[5pt] 9y^2-\left(x^2+6x + 9\right) & = & 10 - 1(9) & \\[5pt] 9y^2-(x+3)^2 & = & 1 & \\[4pt] \dfrac{y^2}{\frac{1}{9}} - \dfrac{(x+3)^2}{1} & = & 1 & \end{array}\nonumber\]
Ahora que esta ecuación está en la forma estándar de la Ecuación 7.7, vemos que\(x-h\) es\(x+3\) así\(h = -3\), y\(y-k\) es\(y\) así\(k = 0\). De ahí que nuestra hipérbola se centre en\((-3, 0)\). Nos parece que\(a^2 = 1\) así\(a=1\), y\(b^2 = \frac{1}{9}\) así\(b=\frac{1}{3}\). Esto significa que movemos\(1\) unidad a la izquierda y derecha del centro y\(\frac{1}{3}\) unidades arriba y abajo desde el centro para llegar a puntos en el rectángulo guía. Ya que el\(x^2\) término se está restando del\(y^2\) término, sabemos que las ramas de la hipérbola se abren hacia arriba y hacia abajo. Esto significa que el eje transversal se encuentra a lo largo de la línea vertical\(x=-3\) y el eje conjugado se encuentra a lo largo del\(x\) eje. Dado que los vértices de la hipérbola son donde la hipérbola se cruza con el eje transversal, obtenemos que los vértices son\(\frac{1}{3}\) de una unidad por encima y por debajo\((-3, 0)\) en\(\left(-3, \frac{1}{3}\right)\) y\(\left(-3, -\frac{1}{3}\right)\). Para encontrar los focos, utilizamos\[c = \sqrt{a^2 + b^2} = \sqrt{\frac{1}{9} + 1} = \frac{\sqrt{10}}{3}\nonumber\] Dado que los focos se encuentran en el eje transversal, movemos\(\frac{\sqrt{10}}{3}\) unidades arriba y abajo\((-3, 0)\) para llegar a\(\left(-3, \frac{\sqrt{10}}{3}\right)\) y\(\left(-3, -\frac{\sqrt{10}}{3}\right)\). Para determinar las asíntotas, recordemos que las asíntotas pasan por el centro de la hipérbola\((-3,0)\),, así como las esquinas del rectángulo guía, por lo que tienen pendientes de\(\pm \frac{b}{a} = \pm \frac{1}{3}\). Usando la ecuación punto-pendiente de una línea, Ecuación 2.2, obtenemos\(y = \frac{1}{3}x + 1\) y\(y = -\frac{1}{3}x - 1\). Poniéndolo todo junto, obtenemos
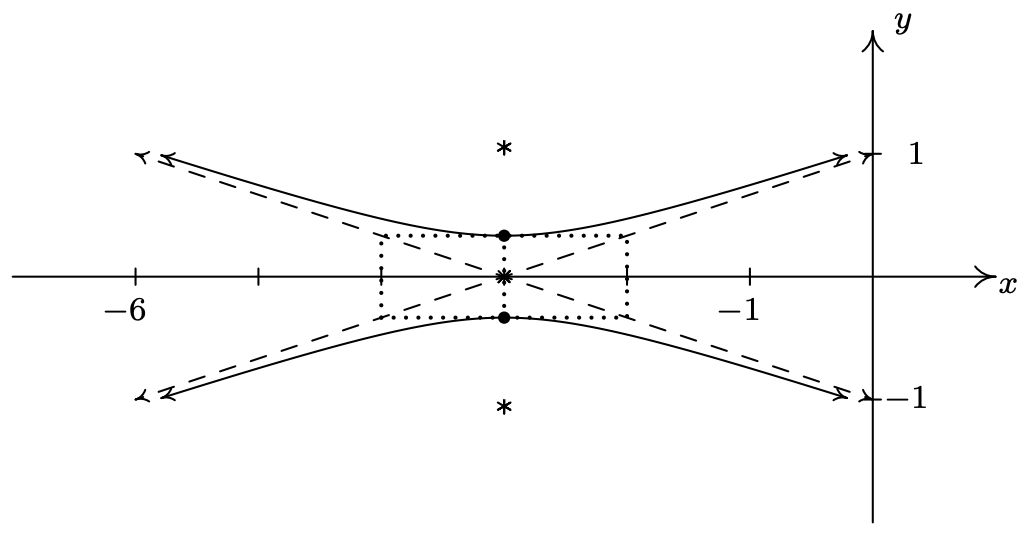
Las hipérbolas se pueden utilizar en los llamados problemas de 'trilateración' o 'posicionamiento'. El procedimiento esbozado en el siguiente ejemplo es la base del sistema LONG Range Aid to Navigation (LORAN para abreviar) (ahora prácticamente desaparecido). 2
Jeff está estacionado\(10\) millas al oeste de Carl en un bosque vacío en un intento de localizar a un esquivo Sasquatch. Al golpe de medianoche, Jeff graba una llamada de Sasquatch\(9\) segundos antes que Carl. Si la velocidad del sonido esa noche es de\(760\) millas por hora, determine un camino hiperbólico a lo largo del cual debe ubicarse Sasquatch.
Solución
Ya que Jeff escucha a Sasquatch antes, está más cerca de Jeff que de Carl. Dado que la velocidad del sonido es de\(760\) millas por hora, podemos determinar cuánto más cerca está Sasquatch de Jeff multiplicando\[760 \, \frac{\mbox{miles}}{\mbox{hour}} \times \frac{ 1 \, \mbox{hour}}{ 3600 \, \mbox{seconds}} \times 9 \, \mbox{seconds} = 1.9 \, \mbox{miles}\nonumber\] Esto significa que Sasquatch está\(1.9\) millas más cerca de Jeff que de Carl. Es decir, Sasquatch debe estar en un camino donde\[\text{(the distance to Carl)} - \text{(the distance to Jeff)} = 1.9\nonumber\] Esta es exactamente la situación en la definición de una hipérbola, Definición 7.6. En este caso, Jeff y Carl se encuentran en los focos, 3 y nuestra distancia fija\(d\) es 1.9. Por simplicidad, asumimos que la hipérbola se centra en\((0,0)\) con sus focos en\((-5, 0)\) y\((5, 0)\). Esquemáticamente, tenemos

Estamos buscando una curva de la forma\(\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1\) en la que se encuentre la distancia desde el centro a cada foco\(c = 5\). Como vimos en la derivación de la ecuación estándar de la hipérbola, Ecuación 7.6,\(d = 2a\), así que\(2a = 1.9\), o\(a = 0.95\) y\(a^2 = 0.9025\). Todo lo que queda es encontrar\(b^2\). Para ello, lo recordamos\(a^2 + b^2 = c^2\) así\(b^2 = c^2 - a^2 = 25 - 0.9025 = 24.0975\). Dado que Sasquatch está más cerca de Jeff que de Carl, debe estar en la rama occidental (mano izquierda) de\(\frac{x^2}{0.9025} - \frac{y^2}{24.0975} = 1\).
En nuestro ejemplo anterior, no teníamos suficiente información para precisar la ubicación exacta de Sasquatch. Para lograrlo, necesitaríamos un tercer observador.
Por un golpe de suerte, Kai también estuvo acampando en el bosque durante los eventos del ejemplo anterior. Fue localizado\(6\) millas al norte de Jeff y escuchó la llamada de Sasquatch\(18\) segundos después de que Jeff lo hiciera. Utilice esta información agregada para localizar a Sasquatch.
Solución
Kai y Jeff son ahora los focos de una segunda hipérbola donde se\(d\) puede determinar la distancia fija como antes\[760 \, \dfrac{\mbox{miles}}{\mbox{hour}} \times \dfrac{ 1 \, \mbox{hour}}{ 3600 \, \mbox{seconds}} \times 18 \, \mbox{seconds} = 3.8 \, \mbox{miles}\nonumber\] Desde que Jeff se posicionó en\((-5, 0)\), colocamos a Kai en\((-5, 6)\). Esto pone el centro de la nueva hipérbola en\((-5, 3)\). Trazar la posición de Kai y el nuevo centro nos da el siguiente diagrama a la izquierda. La segunda hipérbola es vertical, por lo que debe ser de la forma\(\frac{(y-3)^2}{b^2} - \frac{(x+5)^2}{a^2} = 1\). Como antes, la distancia\(d\) es la longitud del eje mayor, que en este caso lo es\(2b\). Nos ponemos\(2b = 3.8\) así que\(b = 1.9\) y\(b^2 = 3.61\). Con Kai\(6\) millas al norte de Jeff, tenemos que la distancia desde el centro hasta el foco es\(c = 3\). Ya que\(a^2 + b^2 = c^2\), obtenemos\(a^2 = c^2 - b^2 = 9 - 3.61 = 5.39\). Kai escuchó el llamado de Sasquatch después de Jeff, así que Kai está más lejos de Sasquatch que Jeff. Así Sasquatch debe estar en la rama sur de la hipérbola\(\frac{(y-3)^2}{3.61} - \frac{(x+5)^2}{5.39} = 1\). Al observar la rama occidental de la hipérbola determinada por Jeff y Carl junto con la rama sur de la hipérbola determinada por Kai y Jeff, vemos que hay exactamente un punto en común, y aquí es donde debió haber estado Sasquatch cuando llamó.
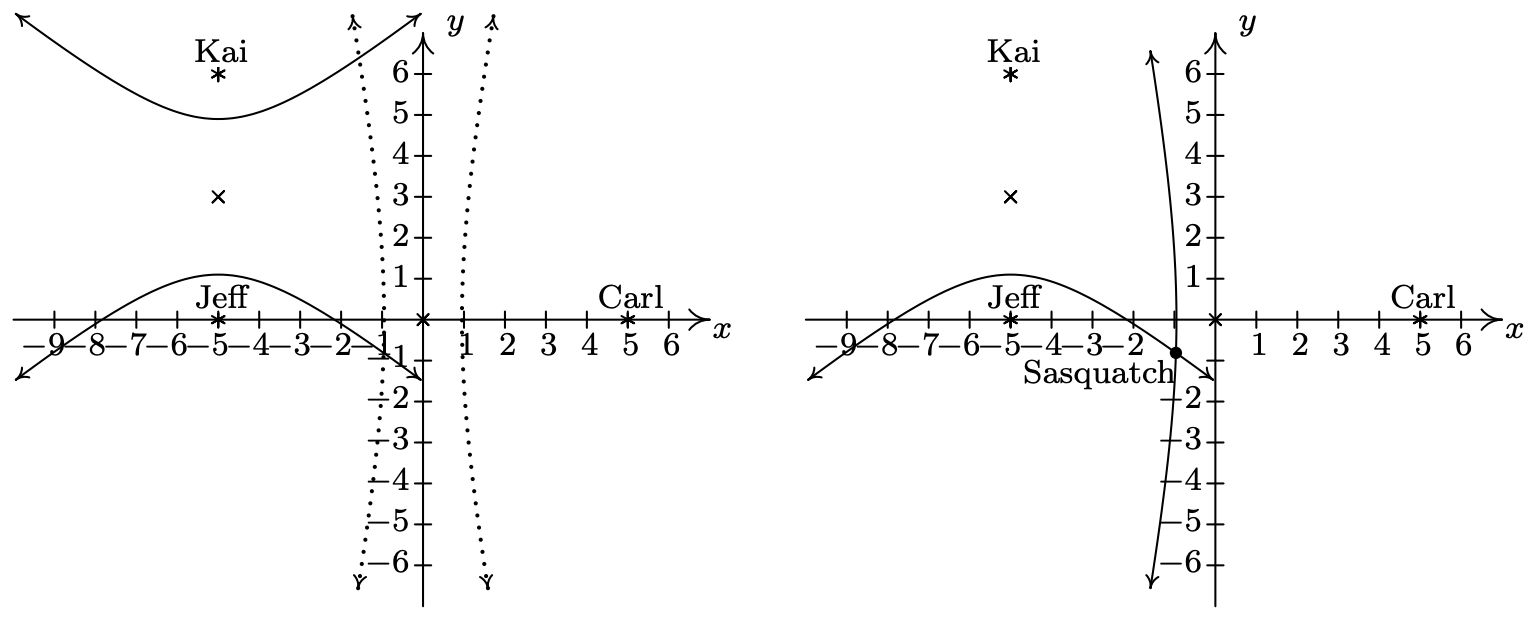
Para determinar exactamente las coordenadas de este punto de intersección, necesitaríamos técnicas para resolver sistemas de ecuaciones no lineales (que no veremos hasta la Sección 8.7), por lo que usamos la calculadora 4 Al hacerlo, obtenemos Sasquatch está aproximadamente a\((-0.9629, -0.8113)\).
Cada una de las secciones cónicas que hemos estudiado en este capítulo resulta de graficar ecuaciones de la forma\(Ax^2 + Cy^2 + Dx + Ey + F = 0\) para diferentes elecciones de\(A\),\(C\),\(D\),\(E\), y 5\(F\). Si bien hemos visto los ejemplos 6 que demuestran cómo convertir una ecuación de esta forma general a una de las formas estándar, cerramos este capítulo con algunos consejos sobre qué forma estándar elegir. 7
Estrategias para identificar secciones cónicas
Supongamos que la gráfica de ecuación\(Ax^2 + Cy^2 + Dx + Ey + F = 0\) es una sección cónica no degenerada. a
- Si solo una variable es cuadrada, la gráfica es una parábola. Poner la ecuación en forma de Ecuación 7.2 (si\(x\) es cuadrada) o Ecuación 7.3 (si\(y\) es cuadrada).
Si ambas variables son al cuadrado, mira los coeficientes de\(x^2\) y\(y^2\),\(A\) y\(B\).
- Si\(A=B\), la gráfica es un círculo. Poner la ecuación en forma de Ecuación 7.1.
- Si\(A \neq B\) pero\(A\) y\(B\) tienen el mismo signo, la gráfica es una elipse. Poner la ecuación en forma de Ecuación 7.4.
- Si\(A\) y\(B\) tienen los diferentes signos, la gráfica es una hipérbola. Poner la ecuación en forma de Ecuación 7.6 o Ecuación 7.7.
a Es decir, una parábola, círculo, elipse o hipérbola — ver Sección 7.1.
7.5.1. Ejercicios
En los Ejercicios 1 - 8, grafica la hipérbola. Encuentra el centro, las líneas que contienen los ejes transversales y conjugados, los vértices, los focos y las ecuaciones de las asíntotas.
- \(\dfrac{x^{2}}{16} - \dfrac{y^{2}}{9} = 1\)
- \(\dfrac{y^{2}}{9} - \dfrac{x^{2}}{16} = 1\)
- \(\dfrac{(x - 2)^{2}}{4} - \dfrac{(y + 3)^{2}}{9} = 1\)
- \(\dfrac{(y - 3)^{2}}{11} - \dfrac{(x - 1)^{2}}{10} = 1\)
- \(\dfrac{(x + 4)^{2}}{16} - \dfrac{(y - 4)^{2}}{1} = 1\)
- \(\dfrac{(x+1)^2}{9} - \dfrac{(y-3)^2}{4} = 1\)
- \(\dfrac{(y+2)^2}{16} - \dfrac{(x-5)^2}{20} = 1\)
- \(\dfrac{(x-4)^2}{8} - \dfrac{(y-2)^2}{18} = 1\)
En los Ejercicios 9 - 12, ponga la ecuación en forma estándar. Encuentra el centro, las líneas que contienen los ejes transversales y conjugados, los vértices, los focos y las ecuaciones de las asíntotas.
- \(12x^{2} - 3y^{2} + 30y - 111 = 0\)
- \(18y^{2} - 5x^{2} + 72y + 30x - 63= 0\)
- \(9x^2-25y^2-54x-50y-169 = 0\)
- \(-6x^2+5y^2-24x+40y+26=0\)
En los Ejercicios 13 - 18, encuentra la forma estándar de la ecuación de la hipérbola que tiene las propiedades dadas.
- Centro\((3, 7)\), Vértice\((3, 3)\), Enfoque\((3, 2)\) [buildhypfirst]
- Vértice\((0, 1)\), Vértice\((8, 1)\), Enfoque\((-3, 1)\)
- Focos\((0, \pm 8)\), Vértices\((0, \pm 5)\).
- Focos\((\pm 5, 0)\), longitud del Eje Conjugado\(6\)
- Vértices\((3,2)\),\((13,2)\); Puntos finales del Eje Conjugado\((8,4)\),\((8,0)\)
- Vértice\((-10, 5)\), asíntotas\(y = \pm \frac{1}{2}(x - 6) + 5\) [buildhyplast]
En los Ejercicios 19 - 28, encuentra la forma estándar de la ecuación usando las pautas de la página y luego grafica la sección cónica.
- \(x^2-2x-4y-11=0\)
- \(x^2 + y^2-8x+4y+11=0\)
- \(9x^2 + 4y^2-36x+24y + 36=0\)
- \(9x^2-4y^2-36x-24y-36=0\)
- \(y^2+8y-4x+16=0\)
- \(4x^2+y^2-8x+4=0\)
- \(4x^2+9y^2-8x+54y+49=0\)
- \(x^2 + y^2-6x+4y+14=0\)
- \(2x^2+ 4y^2+12x-8y+25=0\)
- \(4x^2-5y^2-40x-20y+160=0\)
- La gráfica de una hipérbola vertical u horizontal falla claramente la Prueba de Línea Vertical, Teorema 1.1, por lo que la ecuación de una vertical de hipérbola horizontal no define\(y\) como una función de\(x\). 8 Sin embargo, al igual que con círculos, parábolas horizontales y elipses, podemos dividir una hipérbola en pedazos, cada uno de los cuales\(y\) representaría efectivamente en función de\(x\). Con la ayuda de tus compañeros de clase, usa tu calculadora para graficar las hipérbolas dadas en los Ejercicios 1 - 8 anteriores. ¿Cuántas piezas necesitas para una hipérbola vertical? ¿Cuántos para una hipérbola horizontal?
- La ubicación del epicentro de un sismo,\(-\) el punto en la superficie de la Tierra directamente por encima de donde ocurrió realmente el sismo, se\(-\) puede determinar mediante un proceso similar a como ubicamos a Sasquatch en el Ejemplo 7.5.5. (Como dijimos en el Ejercicio 75 de la Sección 6.1, los sismos son eventos complicados y no es nuestra intención brindar una discusión completa de la ciencia involucrada en ellos. En cambio, remitimos al lector interesado a un curso de Geología o al Programa de Riesgos de Terremotos del Servicio Geológico de Estados Unidos que se encuentra aquí). Nuestra técnica funciona sólo para distancias relativamente pequeñas porque necesitamos asumir que la Tierra es plana para poder utilizar hipérbolas en el plano. 9 Las ondas P (“P” significa Primaria) de un sismo en Sasquatchia viajan a 6 kilómetros por segundo. 10 La Estación A registra primero las olas. Después la Estación B, que está a 100 kilómetros con destino al norte de la Estación A, registra las olas 2 segundos después. La Estación C, que está a 150 kilómetros al oeste de la Estación A registra las olas 3 segundos después de eso (un total de 5 segundos después de la Estación A). ¿Dónde está el epicentro?
- La noción de excentricidad introducida para elipses en la Definición 7.5 en la Sección 7.4 es la misma para las hipérbolas en el sentido de que podemos definir la excentricidad\(e\) de una hipérbola como
\[e = \dfrac{\mbox{distance from the center to a focus}}{\mbox{distance from the center to a vertex}}\nonumber\]
- Con la ayuda de tus compañeros, explica por qué\(e > 1\) para cualquier hipérbola.
- Encuentra la ecuación de la hipérbola con vértices\((\pm 3,0)\) y excentricidad\(e = 2\).
- Con la ayuda de tus compañeros, encuentra la excentricidad de cada una de las hipérbolas en los Ejercicios 1 - 8. ¿Qué papel juega la excentricidad en la forma de las gráficas?
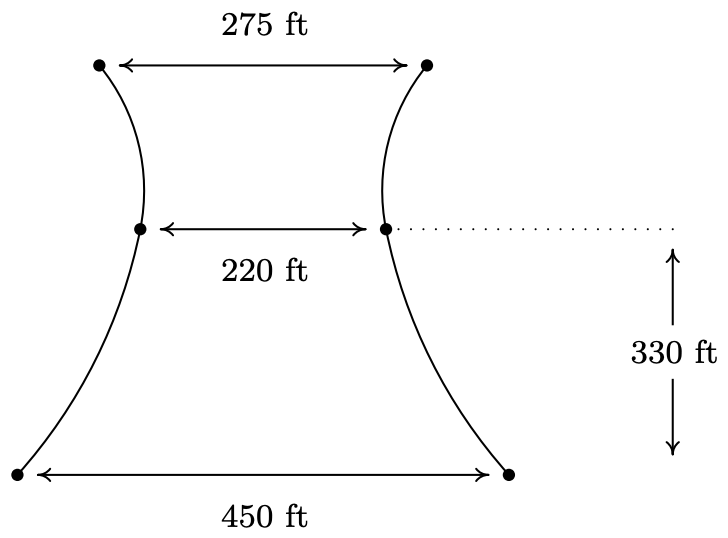
- En la página 510 en la Sección 7.3, discutimos los paraboloides de la revolución al estudiar el diseño de antenas parabólicas y espejos parabólicos. De la misma manera, las torres de enfriamiento de 'tiro natural' suelen tener la forma de hiperboloides de revolución. Cada sección transversal vertical de estas torres es una hipérbola. Supongamos que la torre de enfriamiento de tiro natural tiene la sección transversal a continuación. Supongamos que la torre tiene 450 pies de ancho en la base, 275 pies de ancho en la parte superior y 220 pies en su punto más estrecho (que ocurre 330 pies sobre el suelo). Determinar la altura de la torre al pie más cercano.
- Con la ayuda de tus compañeros, investiga el Telescopio Cassegrain. Utiliza la propiedad reflectante de la hipérbola así como la de la parábola para hacer un ingenioso telescopio.
- [cónicasclasificaciónnoxytermex] Con la ayuda de tus compañeros demuestra que si\(Ax^2 + Cy^2 + Dx + Ey + F = 0\) determina una cónica no degenerada 11 entonces
- \(AC < 0\)significa que la gráfica es una hipérbola
- \(AC = 0\)significa que la gráfica es una parábola
- \(AC > 0\)significa que la gráfica es una elipse o círculo
NOTA: Este resultado será generalizado en el Teorema 11.11 en la Sección 11.6.1.
7.5.2. RESPUESTAS
- \(\dfrac{x^{2}}{16} - \dfrac{y^{2}}{9} = 1\)
Eje\((0, 0)\)
transversal central sobre eje\(y = 0\)
conjugado en\(x = 0\)
vértices\((4, 0), (-4, 0)\)
Focos\((5, 0), (-5, 0)\)
asíntotas\(y = \pm \frac{3}{4} x\)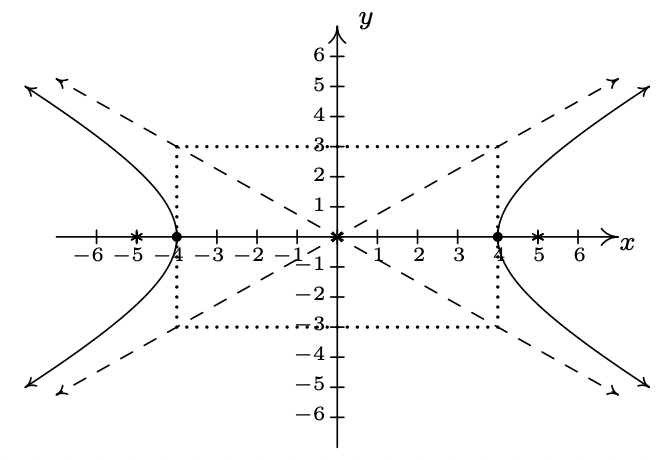
- \(\dfrac{y^{2}}{9} - \dfrac{x^{2}}{16} = 1\)
Eje\((0, 0)\)
transversal central sobre eje\(x = 0\)
conjugado en\(y = 0\)
vértices\((0, 3), (0, -3)\)
Focos\((0, 5), (0, -5)\)
asíntotas\(y = \pm \frac{3}{4} x\)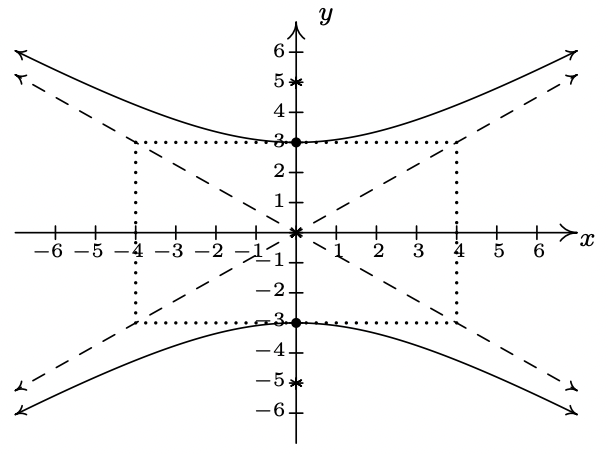
- \(\dfrac{(x - 2)^{2}}{4} - \dfrac{(y + 3)^{2}}{9} = 1\)
Eje\((2, -3)\)
transversal central sobre eje\(y = -3\)
conjugado en\(x = 2\)
vértices\((0, -3), (4, -3)\)
Focos\((2 + \sqrt{13}, -3), (2 - \sqrt{13}, -3)\)
asíntotas\(y = \pm \frac{3}{2}(x - 2) - 3\)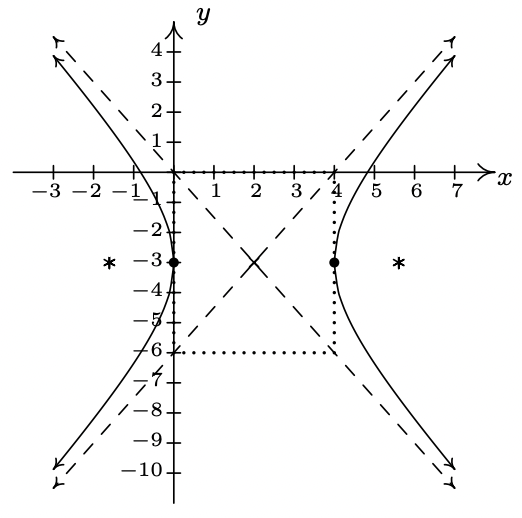
- \(\dfrac{(y - 3)^{2}}{11} - \dfrac{(x - 1)^{2}}{10} = 1\)
Eje\((1, 3)\)
transversal central sobre eje\(x = 1\)
conjugado en\(y = 3\)
vértices\((1, 3 + \sqrt{11}), (1, 3 - \sqrt{11})\)
Focos\((1, 3 + \sqrt{21}), (1, 3 - \sqrt{21})\)
asíntotas\(y = \pm \frac{\sqrt{110}}{10}(x - 1) + 3\)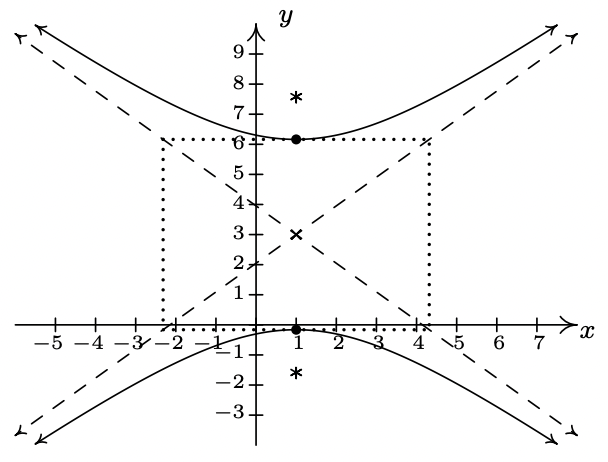
- \(\dfrac{(x + 4)^{2}}{16} - \dfrac{(y - 4)^{2}}{1} = 1\)
Eje\((-4, 4)\)
transversal central sobre eje\(y = 4\)
conjugado en\(x = -4\)
vértices\((-8, 4), (0, 4)\)
Focos\((-4 + \sqrt{17}, 4), (-4 - \sqrt{17}, 4)\)
asíntotas\(y = \pm \frac{1}{4}(x +4) +4\)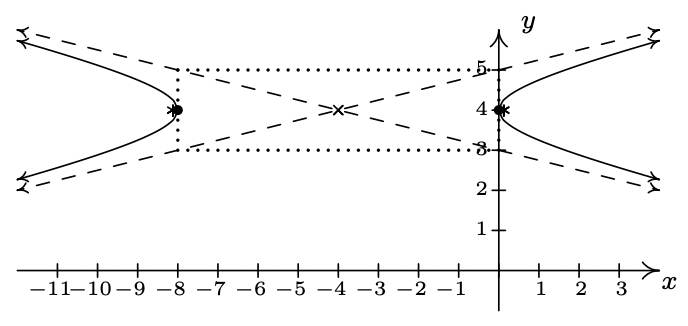
- \(\dfrac{(x+1)^2}{9} - \dfrac{(y-3)^2}{4} = 1\)
Eje\((-1, 3)\)
transversal central sobre eje\(y=3\)
conjugado en\(x=-1\)
vértices\((2, 3), (-4, 3)\)
Focos\(\left(-1+\sqrt{13}, 3\right), \left(-1-\sqrt{13}, 3\right)\)
asíntotas\(y = \pm \frac{2}{3} (x+1)+3\)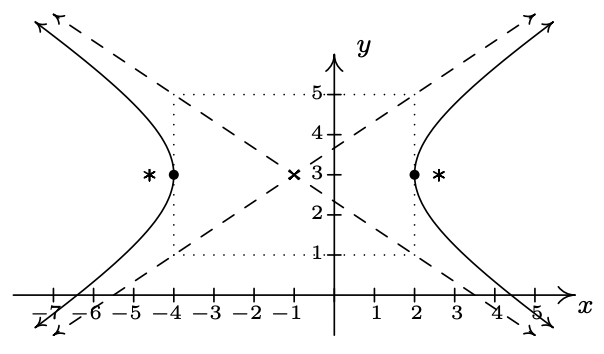
- \(\dfrac{(y+2)^2}{16} - \dfrac{(x-5)^2}{20} = 1\)
Eje\((5, -2)\)
transversal central sobre eje\(x=5\)
conjugado en\(y=-2\)
vértices\((5,2), (5,-6)\)
Focos\(\left(5,4 \right), \left(5,-8\right)\)
asíntotas\(y = \pm \frac{2\sqrt{5}}{5} (x-5)-2\)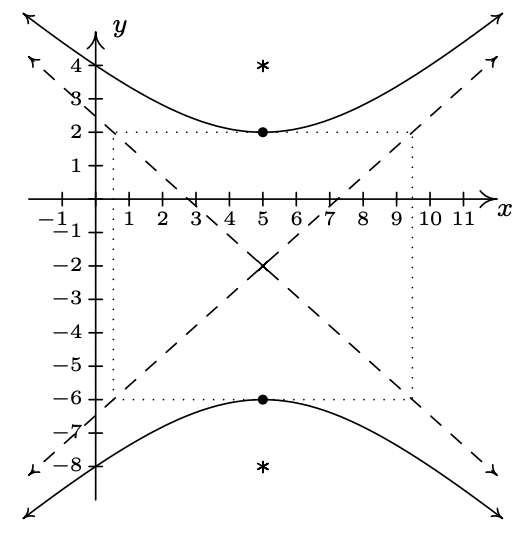
- \(\dfrac{(x-4)^2}{8} - \dfrac{(y-2)^2}{18} = 1\)
Eje\((4, 2)\)
transversal central sobre eje\(y=2\)
conjugado en\(x=4\)
vértices\(\left(4+2\sqrt{2},2\right), \left(4-2\sqrt{2},2\right)\)
Focos\(\left(4+\sqrt{26},2 \right), \left(4-\sqrt{26},2\right)\)
asíntotas\(y = \pm \frac{3}{2} (x-4)+2\)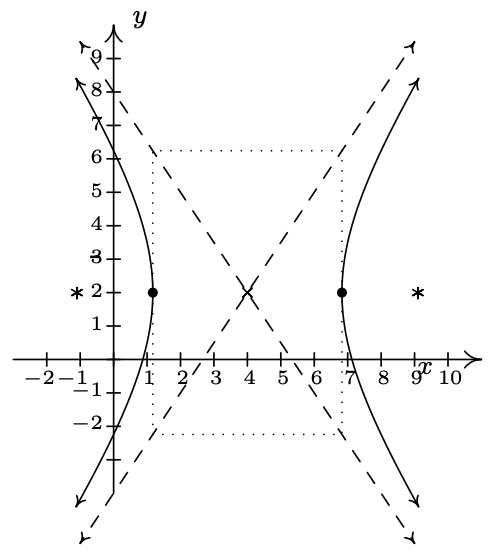
- \(\dfrac{x^{2}}{3} - \dfrac{(y - 5)^{2}}{12} = 1\)
Eje\((0, 5)\)
transversal central sobre eje\(y = 5\)
conjugado en\(x = 0\)
vértices\((\sqrt{3}, 5), (-\sqrt{3}, 5)\)
Focos\((\sqrt{15}, 5), (-\sqrt{15}, 5)\)
asíntotas\(y = \pm 2x + 5\) - \(\dfrac{(y + 2)^{2}}{5} - \dfrac{(x - 3)^{2}}{18} = 1\)
Eje\((3, -2)\)
transversal central sobre eje\(x = 3\)
conjugado en\(y = -2\)
vértices\((3, -2 + \sqrt{5}), (3, -2 - \sqrt{5})\)
Focos\((3, -2 + \sqrt{23}), (3, -2 - \sqrt{23})\)
asíntotas\(y = \pm \frac{\sqrt{10}}{6}(x - 3) - 2\) - \(\dfrac{(x-3)^{2}}{25} - \dfrac{(y+1)^{2}}{9} = 1\)
Eje\((3, -1)\)
transversal central sobre eje\(y=-1\)
conjugado en\(x=3\)
vértices\((8, -1), (-2, -1)\)
Focos\(\left(3+\sqrt{34}, -1 \right), \left(3-\sqrt{34}, -1 \right)\)
asíntotas\(y = \pm \frac{3}{5}(x - 3) - 1\) - \(\dfrac{(y+4)^{2}}{6} - \dfrac{(x+2)^{2}}{5} = 1\)
Eje\((-2, -4)\)
transversal central sobre eje\(x=-2\)
conjugado en\(y=-4\)
vértices\(\left(-2,-4+\sqrt{6} \right), \left(-2,-4-\sqrt{6} \right)\)
Focos\(\left(-2, -4+\sqrt{11} \right), \left(-2, -4-\sqrt{11} \right)\)
asíntotas\(y = \pm \frac{\sqrt{30}}{5}(x + 2) - 4\) - \(\dfrac{(y - 7)^{2}}{16} - \dfrac{(x - 3)^{2}}{9} = 1\)
- \(\dfrac{(x - 4)^{2}}{16} - \dfrac{(y - 1)^{2}}{33} = 1\)
- \(\dfrac{y^{2}}{25} - \dfrac{x^{2}}{39} = 1\)
- \(\dfrac{x^{2}}{16} - \dfrac{y^{2}}{9} = 1\)
- \(\dfrac{(x - 8)^{2}}{25} - \dfrac{(y - 2)^{2}}{4} = 1\)
- \(\dfrac{(x - 6)^{2}}{256} - \dfrac{(y - 5)^{2}}{64} = 1\)
- \((x-1)^2 = 4(y+3)\)
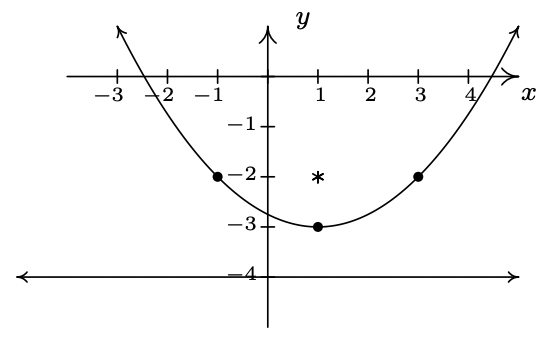
- \((x-4)^2+(y+2)^2 = 9\)
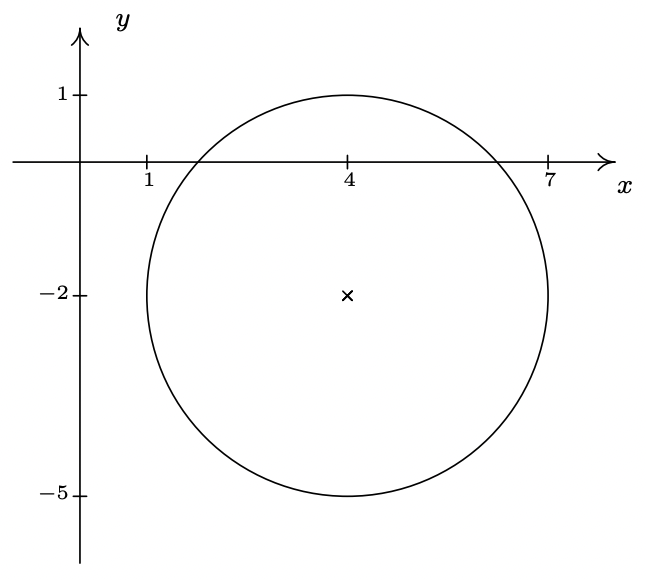
- \(\dfrac{(x - 2)^{2}}{4} + \dfrac{(y + 3)^{2}}{9} = 1\)
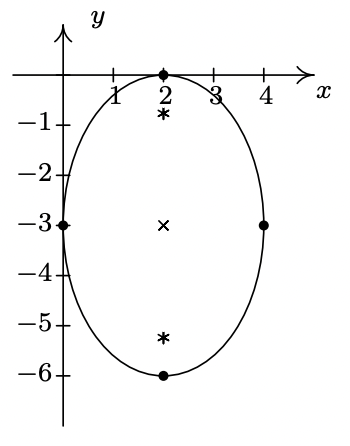
- \(\dfrac{(x - 2)^{2}}{4} - \dfrac{(y + 3)^{2}}{9} = 1\)
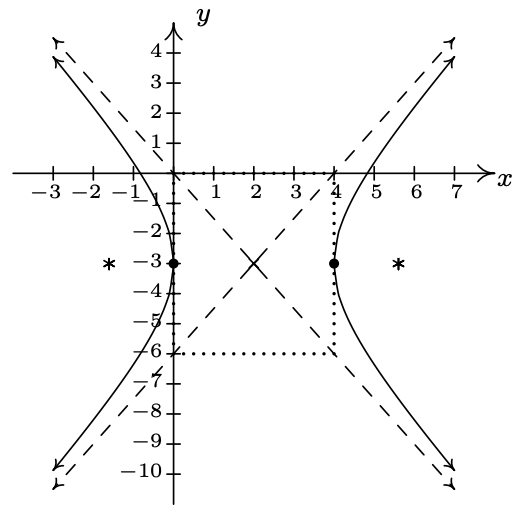
- \((y + 4)^{2} = 4x\)
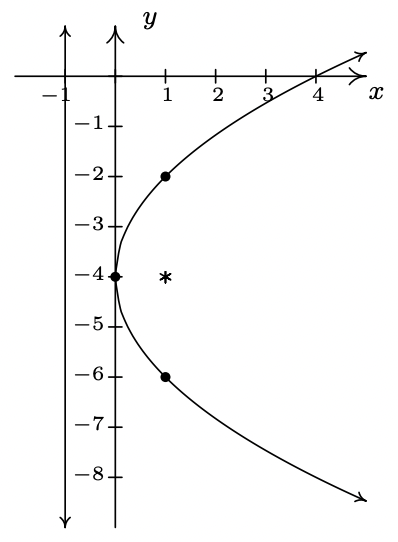
-
\(\dfrac{(x-1)^2}{1}+\dfrac{y^2}{4}=0\)
La gráfica es\((1,0)\) solo el punto. - \(\dfrac{(x-1)^2}{9}+\dfrac{(y+3)^2}{4} = 1\)
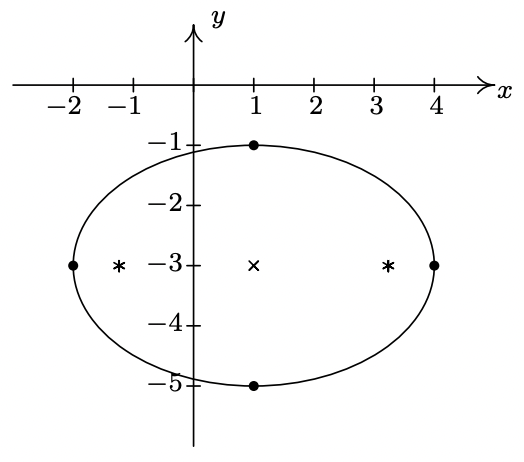
-
\((x-3)^2+(y+2)^2=-1\)
No hay gráfica. -
\(\dfrac{(x+3)^2}{2}+\dfrac{(y-1)^2}{1} = -\dfrac{3}{4}\)
No hay gráfica. - \(\dfrac{(y+2)^2}{16} - \dfrac{(x-5)^2}{20} = 1\)
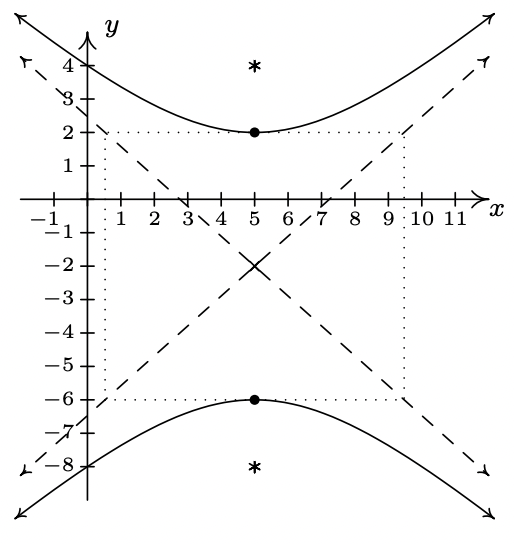
- Al colocar la Estación A en\((0, -50)\) y la Estación B en\((0, 50)\), la diferencia de tiempo de dos segundos produce la hipérbola\(\frac{y^{2}}{36} - \frac{x^{2}}{2464} = 1\) con focos A y B y centro\((0, 0)\). Colocar la Estación C en\((-150, -50)\) y usando los focos A y C nos da un centro de\((-75, -50)\) y la hipérbola\(\frac{(x + 75)^{2}}{225} - \frac{(y + 50)^{2}}{5400} = 1\). El punto de intersección de estas dos hipérbolas que está más cerca de A que B y más cercano a A que C es\((-57.8444, -9.21336)\) así que es el epicentro.
- \(\dfrac{x^2}{9} - \dfrac{y^2}{27} = 1\).
- La torre puede ser modelada (aproximadamente) 12 por\(\frac{x^2}{12100} - \frac{(y-330)^2}{34203} = 1\). Para encontrar la altura, enchufamos en\(x = 137.5\) qué rendimientos\(y \approx 191\) o\(y \approx 469\). Dado que la parte superior de la torre está por encima del punto más estrecho, obtenemos que la torre mide aproximadamente 469 pies de altura.
Referencia
1 Es un buen ejercicio para resolver realmente esto.
2 El GPS ahora gobierna el reino de posicionamiento. ¿Todavía hay lugar para LORAN y otros sistemas terrestres? ¿Los satélites alguna vez funcionan mal?
3 Normalmente nos gusta ser el centro de atención, pero ser el foco de atención funciona igual de bien.
4 Primero resuelve cada hipérbola para\(y\), y elige la ecuación correcta (rama) antes de continuar.
5 Consulte la Sección 11.6 para ver por qué nos saltamos\(B\).
6 Ejemplos 7.2.3, 7.3.4, 7.4.3 y 7.5.3, en particular.
7 Formalizamos esto en el Ejercicio 34.
8 Veremos más adelante en el texto que las gráficas de ciertas hipérbolas giradas pasan la Prueba de Línea Vertical.
9 De vuelta en los Ejercicios en la Sección 1.1 se te pidió que investigaras a personas que creen que el mundo es plano. ¿Qué descubriste?
10 Dependiendo de la composición de la corteza en una ubicación específica, las ondas P pueden viajar entre 5 kps y 8 kps.
11 Recordemos que esto significa que su gráfica es o bien un círculo, una parábola, una elipse o una hipérbola.
12 El valor exacto debajo\((y-330)^{2}\) es\(\frac{52707600}{1541}\) en caso de que necesites más precisión.


