7.4: Elipses

En la definición de círculo, Definición 7.1, fijamos un punto llamado centro y consideramos todos los puntos que estaban a una$r$ distancia fija de ese punto. Para nuestra siguiente sección cónica, la elipse, fijamos dos puntos distintos y una distancia$d$ para usar en nuestra definición.

Definición 7.4

Dados dos puntos distintos$F_{1}$ y$F_{2}$ en el plano y una distancia fija$d$, una elipse es el conjunto de todos los puntos$(x, y)$ en el plano tal que la suma de cada una de las distancias desde$F_{1}$ y$F_{2}$ hacia$(x, y)$ es$d$. Los puntos$F_{1}$ y$F_{2}$ se llaman los focos ^a de la elipse.

---

^a el plural de 'focus'

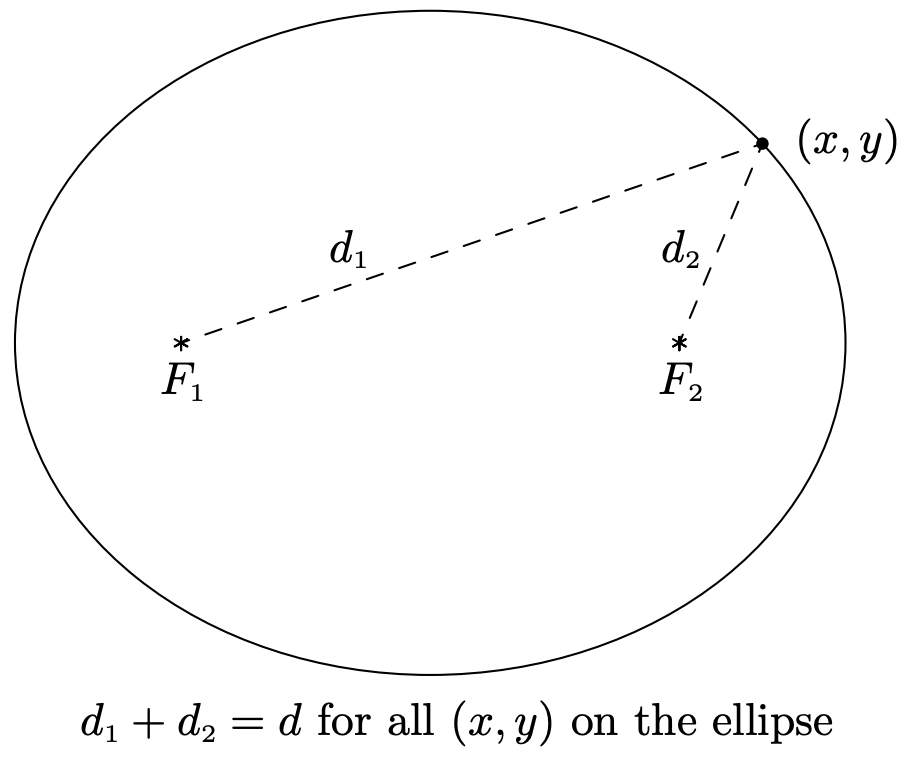
Podemos imaginarnos tomando un largo de cuerda y anclándolo a dos puntos en una hoja de papel. La curva trazada tomando un lápiz y moviéndolo para que la cuerda esté siempre tensa es una elipse.

El centro de la elipse es el punto medio del segmento de línea que conecta los dos focos. El eje principal de la elipse es el segmento de línea que conecta dos extremos opuestos de la elipse que también contiene el centro y los focos. El eje menor de la elipse es el segmento de línea que conecta dos extremos opuestos de la elipse que contiene el centro pero es perpendicular al eje mayor. Los vértices de una elipse son los puntos de la elipse que se encuentran en el eje mayor. Observe que el centro es también el punto medio del eje mayor, de ahí que sea el punto medio de los vértices. En fotos tenemos,

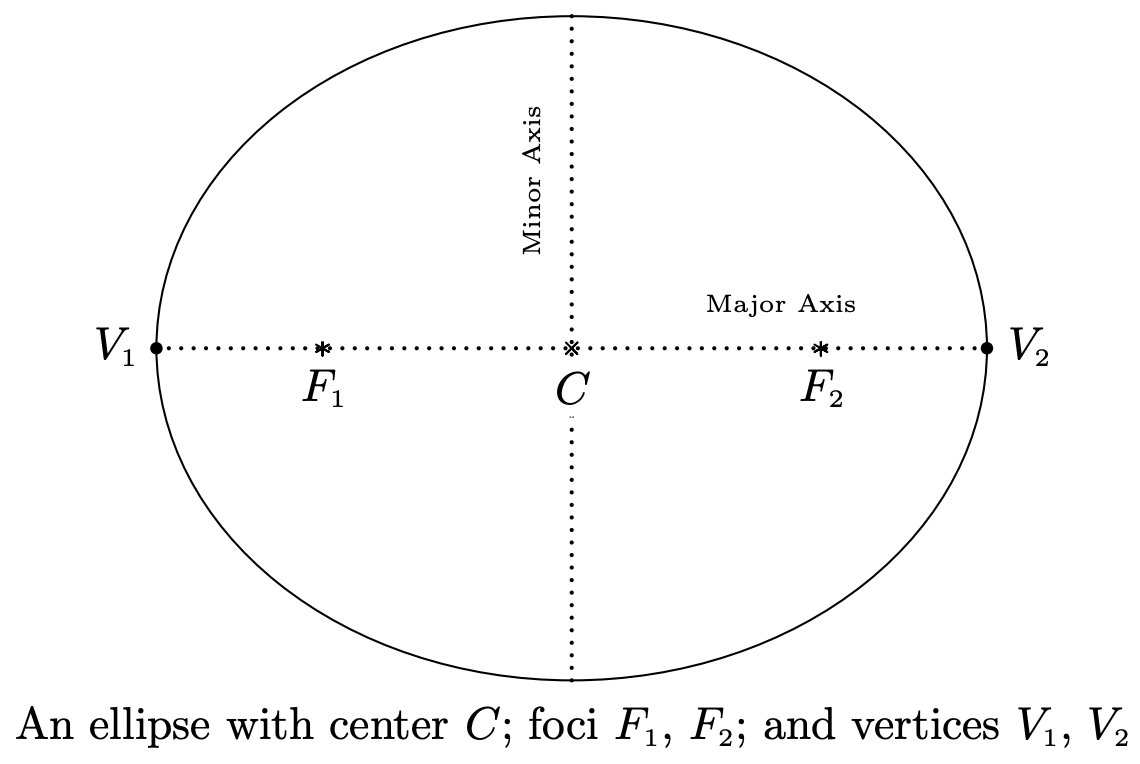
Tenga en cuenta que el eje mayor es el más largo de los dos ejes a través del centro, y de igual manera, el eje menor es el más corto de los dos. Para derivar la ecuación estándar de una elipse, asumimos que la elipse tiene su centro en$(0,0)$, su eje mayor a lo largo del$x$ eje -eje, y tiene focos$(c,0)$ y$(-c,0)$ y vértices$(-a,0)$ y$(a,0)$. Etiquetaremos las$y$ -intercepciones de la elipse como$(0,b)$ y$(0,-b)$ (Asumimos$a$,$b$, y todos$c$ son números positivos.) Esquemáticamente,

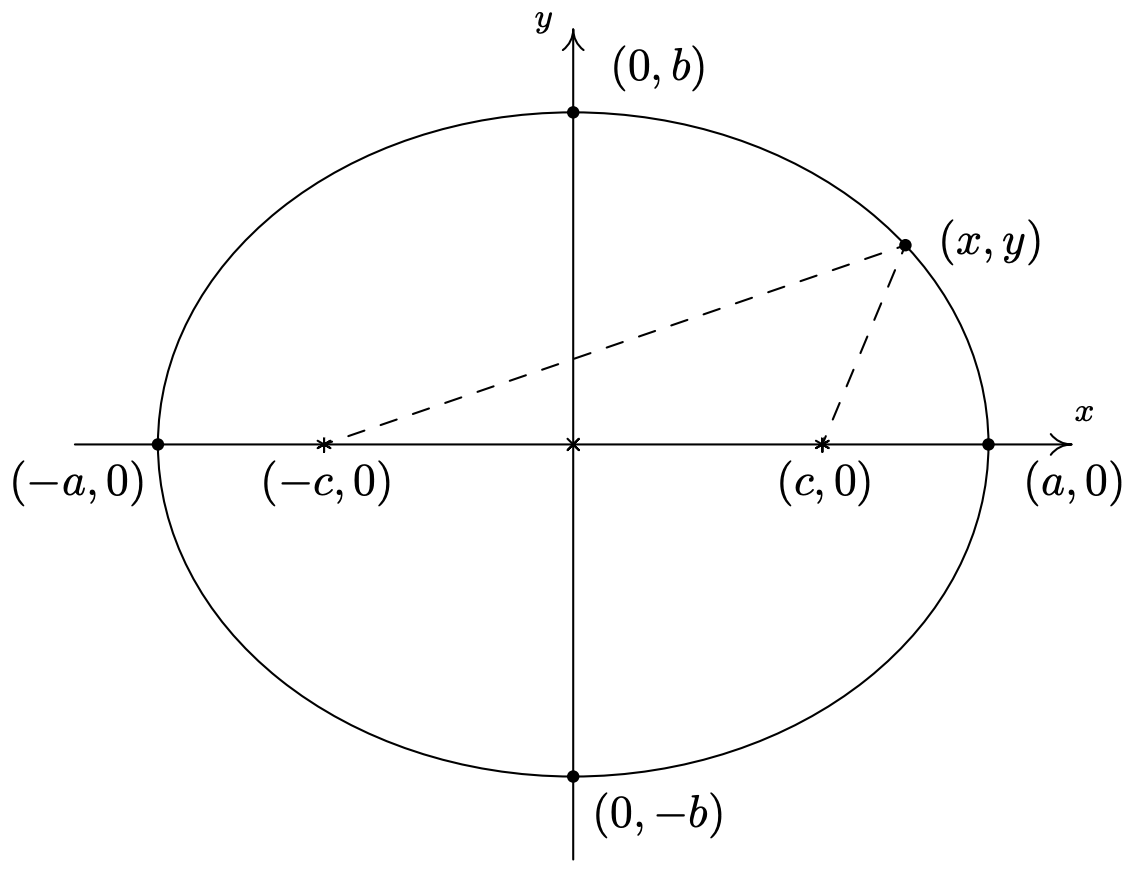
Tenga en cuenta que dado que$(a,0)$ está en la elipse, debe cumplir las condiciones de la Definición 7.4. Es decir, la distancia de$(-c,0)$ a$(a,0)$ más la distancia de$(c,0)$ a$(a,0)$ debe ser igual a la distancia fija$d$. Dado que todos estos puntos se encuentran en el$x$ eje, obtenemos

$$\begin{array}{rclr} \mbox{distance from $(-c,0)$ to $(a,0)$} + \mbox{distance from $(c,0)$ to $(a,0)$} & = & d & \\ (a+c) + (a-c) & = & d & \\ 2a & = & d \\ \end{array}\nonumber$$

Es decir, la distancia fija$d$ mencionada en la definición de elipse no es otra que la longitud del eje mayor. Ahora usamos ese hecho$(0,b)$ está en la elipse, junto con el hecho de que$d=2a$ para obtener

$$\begin{array}{rclr} \mbox{distance from $(-c,0)$ to $(0,b)$} + \mbox{distance from $(c,0)$ to $(0,b)$} & = & 2a & \\ \sqrt{(0-(-c))^2+(b-0)^2} + \sqrt{(0-c)^2+(b-0)^2} & = & 2a & \\ \sqrt{b^2+c^2}+\sqrt{b^2+c^2} & = & 2a \\ 2 \sqrt{b^2+c^2} & = & 2a \\ \sqrt{b^2+c^2} & = & a \end{array}\nonumber$$

A partir de esto, obtenemos$a^2 = b^2 + c^2$, o$b^2 = a^2 - c^2$, que resultará útil más adelante. Ahora considera un punto$(x,y)$ en la elipse. Aplicando la Definición 7.4, obtenemos

$$\begin{array}{rclr} \mbox{distance from $(-c,0)$ to $(x,y)$} + \mbox{distance from $(c,0)$ to $(x,y)$} & = & 2a & \\ \sqrt{(x-(-c))^2+(y-0)^2} + \sqrt{(x-c)^2+(y-0)^2} & = & 2a & \\ \sqrt{(x+c)^2+y^2}+\sqrt{(x-c)^2+y^2} & = & 2a \\ \end{array}\nonumber$$

Para darle sentido a esta situación, necesitamos hacer un buen uso del Álgebra Intermedia.

$$\begin{array}{rclr} \sqrt{(x+c)^2+y^2}+\sqrt{(x-c)^2+y^2} & = & 2a & \\ \sqrt{(x+c)^2+y^2} & = & 2a - \sqrt{(x-c)^2+y^2} & \\ \left(\sqrt{(x+c)^2+y^2}\right)^2 & = & \left(2a - \sqrt{(x-c)^2+y^2}\right)^2 & \\ (x+c)^2+y^2 & = & 4a^2 - 4a\sqrt{(x-c)^2+y^2} + (x-c)^2+y^2 & \\ 4a\sqrt{(x-c)^2+y^2} & = & 4a^2 + (x-c)^2 - (x+c)^2 & \\ 4a\sqrt{(x-c)^2+y^2} & = & 4a^2 - 4cx & \\ a\sqrt{(x-c)^2+y^2} & = & a^2 - cx & \\ \left(a\sqrt{(x-c)^2+y^2}\right)^2 & = & \left(a^2 - cx\right)^2 & \\ a^2\left((x-c)^2+y^2\right) & = & a^4 - 2a^2cx +c^2 x^2 & \\ a^2x^2 - 2a^2cx + a^2c^2+a^2 y^2 & = & a^4 - 2a^2cx +c^2 x^2 & \\ a^2x^2 - c^2 x^2 +a^2 y^2 & = & a^4 - a^2c^2 & \\ \left(a^2 - c^2\right) x^2 +a^2 y^2 & = & a^2 \left(a^2 - c^2\right) & \\ \end{array}\nonumber$$

Estamos casi terminados. Recordemos que$b^2 = a^2 - c^2$ para que

$$\begin{array}{rclr} \left(a^2 - c^2\right)x^2 +a^2 y^2 & = & a^2\left(a^2 - c^2\right) & \\ b^2 x^2 +a^2 y^2 & = & a^2 b^2 & \\ \dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} & = & 1 & \\ \end{array}\nonumber$$

Esta ecuación es para una elipse centrada en el origen. Para obtener la fórmula de la elipse centrada en$(h,k)$, podríamos usar las transformaciones de la Sección 1.7 o volver a derivar la ecuación usando la Definición 7.4 y la fórmula de distancia para obtener la fórmula a continuación.

Ecuación 7.4. La ecuación estándar de una elipse

La ecuación estándar de una elipse: para números desiguales positivos$a$ y$b$, la ecuación de una elipse con centro$(h,k)$ es

$$\dfrac{(x-h)^2}{a^2} + \dfrac{(y-k)^2}{b^2} = 1\nonumber$$

Algunos comentarios sobre la Ecuación 7.4 están en orden. Primero tenga en cuenta que los valores$a$ y$b$ determinan qué tan lejos en las$y$ direcciones$x$ y, respectivamente, se cuenta desde el centro para llegar a puntos en la elipse. También toma nota que si$a > b$, entonces tenemos una elipse cuyo eje mayor es horizontal, y de ahí, los focos se encuentran a la izquierda y derecha del centro. En este caso, como hemos visto en la derivación, la distancia desde el centro hasta el foco,$c$, se puede encontrar por$c = \sqrt{a^2 - b^2}$. Si$b > a$, los roles de los ejes mayor y menor se invierten, y los focos se encuentran por encima y por debajo del centro. En este caso,$c = \sqrt{b^2 - a^2}$. En cualquier caso,$c$ es la distancia desde el centro a cada foco, y$c = \sqrt{\mbox{bigger denominator} - \mbox{smaller denominator}}$. Por último, cabe mencionar que si tomamos la ecuación estándar de un círculo, la Ecuación 7.1, y dividimos ambos lados por$r^2$, obtenemos

Ecuación 7.5. La ecuación estándar alternativa de un círculo

La ecuación estándar alternativa de un círculo: La ecuación de un círculo con centro$(h,k)$ y radio$r >0$ es

$$\dfrac{(x-h)^2}{r^2} + \dfrac{(y-k)^2}{r^2} = 1\nonumber$$

Observe la similitud entre la Ecuación 7.4 y la Ecuación 7.5. Ambas ecuaciones implican una suma de cuadrados igual a$1$; la diferencia es que con un círculo, los denominadores son los mismos, y con una elipse, son diferentes. Si tomamos un enfoque transformacional, podemos considerar tanto las Ecuaciones 7.4 como 7.5 como desplazamientos y estiramientos del Círculo Unitario$x^2 + y^2 = 1$ en la Definición 7.2. Reemplazar$x$ con$(x-h)$ y$y$ con$(y-k)$ causa los habituales desplazamientos horizontales y verticales. Sustituir$x$ con$\frac{x}{a}$ y$y$ con$\frac{y}{b}$ causas los estiramientos verticales y horizontales habituales. En otras palabras, está perfectamente bien pensar en una elipse como la deformación de un círculo en el que el círculo se estira más en una dirección que en la otra. ¹

Ejemplo 7.4.1

Gráfica$\frac{(x+1)^2}{9} + \frac{(y-2)^2}{25} = 1$. Encuentra el centro, las líneas que contienen los ejes mayor y menor, los vértices, los extremos del eje menor y los focos.

Solución

Vemos que esta ecuación está en la forma estándar de la Ecuación 7.4. Aquí$x-h$ es$x+1$ así$h = -1$, y$y-k$ es$y-2$ así$k = 2$. De ahí que nuestra elipse esté centrada en$(-1,2)$. Vemos eso$a^2 = 9$ así$a=3$, y$b^2 = 25$ así$b=5$. Esto significa que movemos$3$ unidades a izquierda y derecha desde el centro y$5$ unidades hacia arriba y hacia abajo desde el centro para llegar a puntos en la elipse. Como ayuda para dibujar, dibujamos un rectángulo que coincide con esta descripción, llamado rectángulo guía, y dibujamos la elipse dentro de este rectángulo como se ve abajo a la izquierda.

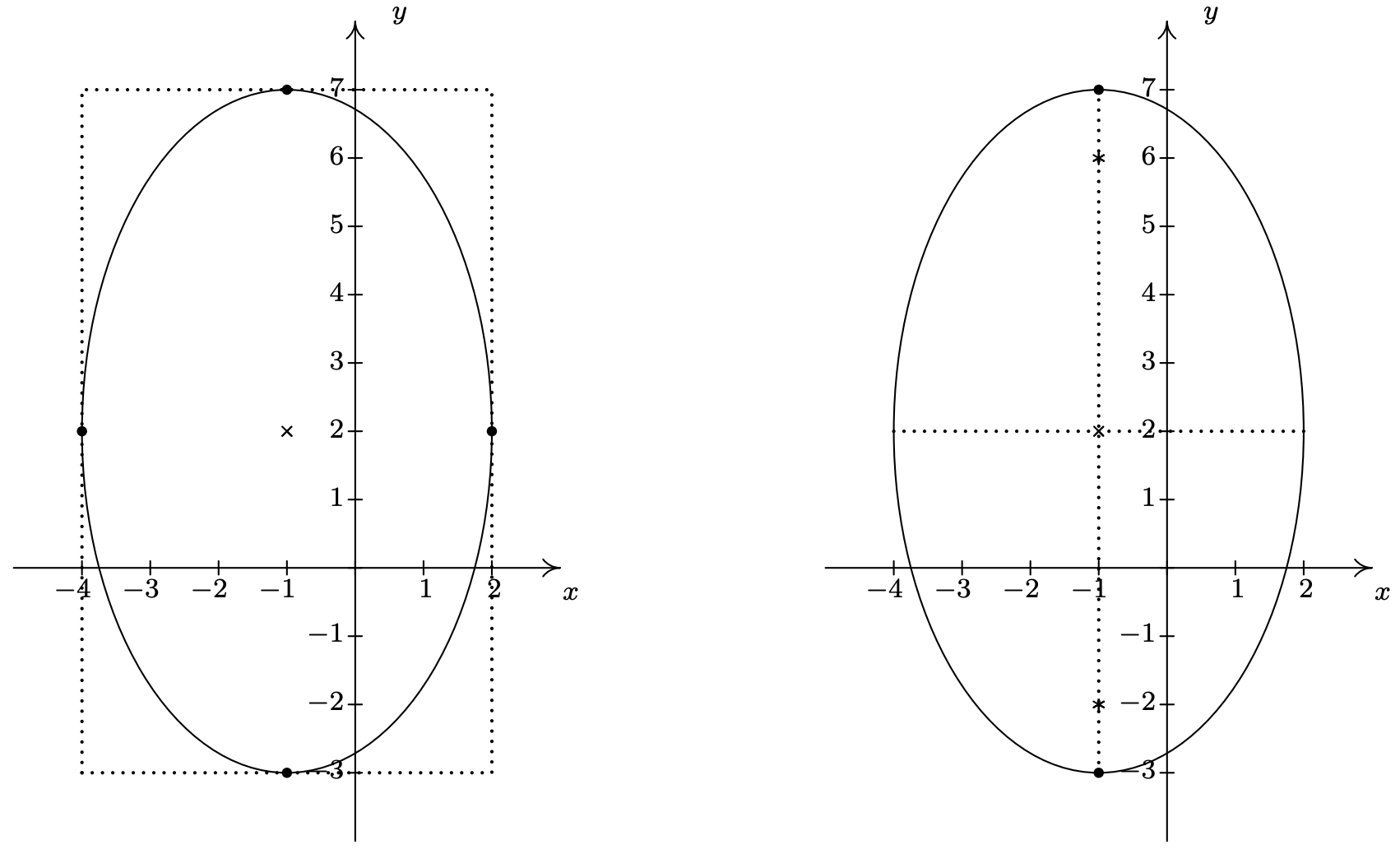
Dado que nos movimos más en la$y$ dirección que en la$x$ dirección, el eje mayor se ubicará a lo largo de la línea vertical$x=-1$, lo que significa que el eje menor se encuentra a lo largo de la línea horizontal,$y = 2$. Los vértices son los puntos en la elipse que se encuentran a lo largo del eje mayor por lo que en este caso, son los puntos$(-1,7)$ y$(-1,-3)$, y los puntos finales del eje menor son$(-4,2)$ y$(2,2)$. (Observe que estos puntos son los cuatro puntos que usamos para dibujar el rectángulo guía). Para encontrar los focos, encontramos$c = \sqrt{25-9} = \sqrt{16} = 4$, lo que significa que los focos se encuentran$4$ unidades desde el centro. Dado que el eje mayor es vertical, los focos se encuentran$4$ unidades por encima y por debajo del centro, en$(-1,-2)$ y$(-1,6)$. Trazar toda esta información da la gráfica que se ve arriba a la derecha.

Ejemplo 7.4.2

Encuentra la ecuación de la elipse con focos$(2,1)$ y$(4,1)$ y vértice$(0,1)$.

Solución

Trazando los datos que nos han dado, tenemos

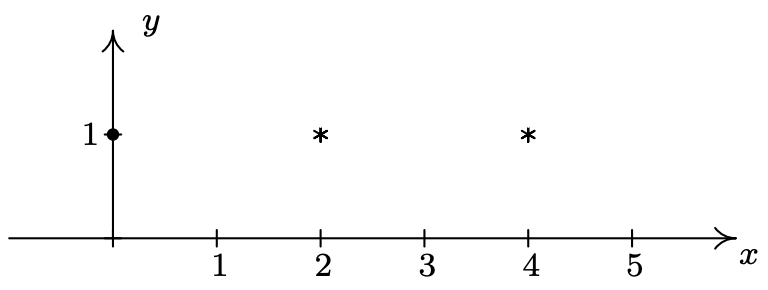
A partir de este bosquejo, sabemos que el eje mayor es horizontal, es decir$a > b$. Ya que el centro es el punto medio de los focos, sabemos que lo es$(3, 1)$. Ya que un vértice es$(0,1)$ tenemos eso$a = 3$, entonces$a^2 = 9$. Todo lo que queda es encontrar$b^2$. Ya que los focos están a$1$ unidad lejos del centro, lo sabemos$c=1$. Ya que$a > b$, tenemos$c = \sqrt{a^2-b^2}$, o$1 = \sqrt{9-b^2}$, así$b^2 = 8$. Sustituyendo todos nuestros hallazgos en la ecuación$\frac{(x-h)^2}{a^2} + \frac{(y-k)^2}{b^2} = 1$, obtenemos nuestra respuesta final para ser$\frac{(x-3)^2}{9}+\frac{(y-1)^2}{8}=1$.

Al igual que con los círculos y las parábolas, se puede dar una ecuación que es una elipse, pero no está en la forma estándar de la Ecuación 7.4. En esos casos, como con círculos y parábolas antes, necesitaremos masajear la ecuación dada en la forma estándar.

Para escribir la ecuación de una elipse en forma estándar

1. Agrupe las mismas variables en un lado de la ecuación y posicione la constante en el otro lado.
2. Completar el cuadrado en ambas variables según sea necesario.
3. Dividir ambos lados por el término constante para que se convierta la constante del otro lado de la ecuación$1$.

Ejemplo 7.4.3

Gráfica$x^2+4y^2-2x+24y+33 = 0$. Encuentra el centro, las líneas que contienen los ejes mayor y menor, los vértices, los extremos del eje menor y los focos.

Solución

Ya que tenemos una suma de cuadrados y los términos cuadrados tienen coeficientes desiguales, es una buena apuesta que tenemos una elipse en nuestras manos. ² Tenemos que completar ambos cuadrados, y luego dividir, si es necesario, para obtener el lado derecho igual a$1$.

$$\begin{array}{rclr} x^2+4y^2-2x+24y+33 & = & 0 & \\ x^2-2x+4y^2+24y & = & -33 & \\ x^2 - 2x + 4\left(y^2+6y\right) & = & - 33 & \\ \left(x^2 - 2x +1\right) + 4\left(y^2+6y+9\right) & = & - 33 + 1 + 4(9)& \\ (x-1)^2 + 4(y+3)^2 & = & 4 & \\[5pt] \dfrac{(x-1)^2 + 4(y+3)^2}{4} & = & \dfrac{4}{4} & \\[10pt] \dfrac{(x-1)^2}{4} + (y+3)^2 & = & 1 & \\[10pt] \dfrac{(x-1)^2}{4} + \dfrac{(y+3)^2}{1} & = & 1 & \\ \end{array}\nonumber$$

Ahora que esta ecuación está en la forma estándar de la Ecuación 7.4, vemos que$x-h$ es$x-1$ así$h = 1$, y$y-k$ es$y+3$ así$k = -3$. De ahí que nuestra elipse esté centrada en$(1,-3)$. Vemos eso$a^2 = 4$ así$a=2$, y$b^2 = 1$ así$b=1$. Esto significa que movemos$2$ las unidades a izquierda y derecha desde el centro y la$1$ unidad hacia arriba y hacia abajo desde el centro para llegar a puntos en la elipse. Dado que nos movimos más en la$x$ dirección que en la$y$ dirección, el eje mayor se ubicará a lo largo de la línea horizontal$y=-3$, lo que significa que el eje menor se encuentra a lo largo de la línea vertical$x = 1$. Los vértices son los puntos en la elipse que se encuentran a lo largo del eje mayor por lo que en este caso, son los puntos$(-1,-3)$ y$(3,-3)$, y los puntos finales del eje menor son$(1,-2)$ y$(1,-4)$. Para encontrar los focos, encontramos$c = \sqrt{4-1} = \sqrt{3}$, lo que significa que los focos se encuentran$\sqrt{3}$ unidades desde el centro. Dado que el eje mayor es horizontal, los focos se encuentran$\sqrt{3}$ unidades a la izquierda y derecha del centro, en$(1-\sqrt{3},-3)$ y$(1+\sqrt{3},-3)$. Trazar toda esta información da

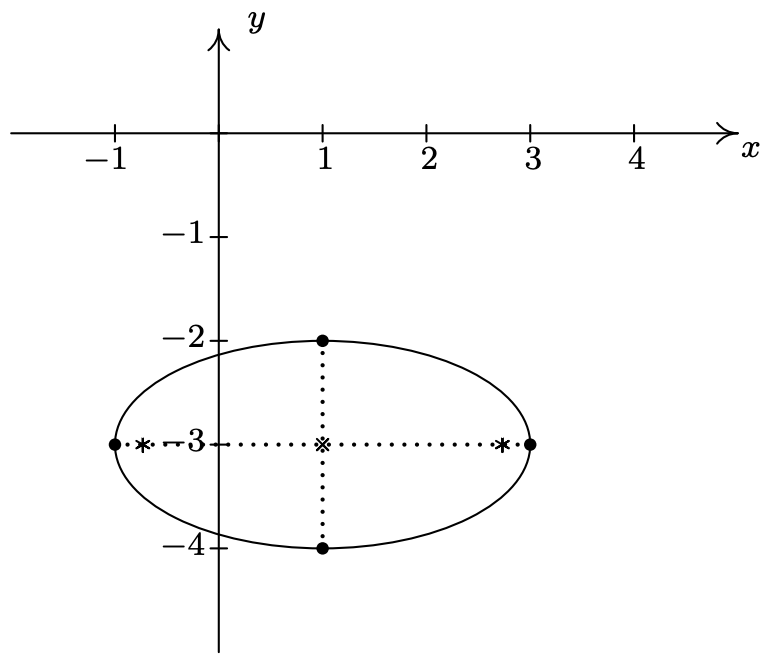
A medida que te encuentres con elipses en los ejercicios de tarea y en la naturaleza, notarás que vienen en todas las formas en tamaños. Compara las dos elipses a continuación.

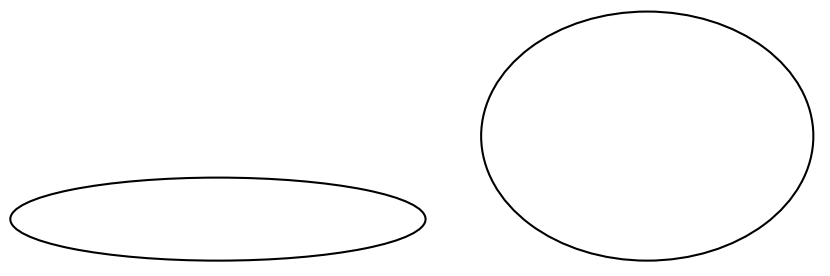
Ciertamente, una elipse es más redonda que la otra. Esta noción de 'redondez' se cuantifica a continuación.

Definición 7.5

La excentricidad de una elipse, denotada$e$, es la siguiente relación:

$$e = \dfrac{\mbox{distance from the center to a focus}}{\mbox{distance from the center to a vertex}}\nonumber$$

En una elipse, los focos están más cerca del centro que los vértices, entonces$0 < e < 1$. La elipse de arriba a la izquierda tiene excentricidad$e \approx 0.98$; para la elipse de arriba a la derecha,$e \approx 0.66$. En general, cuanto más cerca está la excentricidad$0$, más 'circular' es la elipse; cuanto más cerca está la excentricidad$1$, más 'excéntrica' es la elipse.

Ejemplo 7.4.4

Encuentra la ecuación de la elipse cuyos vértices están$(\pm 5,0 )$ con excentricidad$e = \frac{1}{4}$.

Solución

Como antes, trazamos los datos que nos dieron

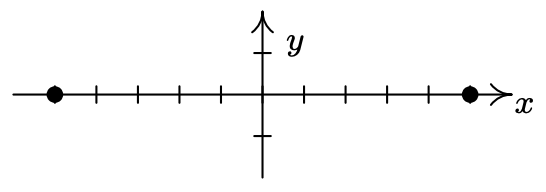
A partir de este bosquejo, sabemos que el eje mayor es horizontal, es decir$a > b$. Con los vértices ubicados en$(\pm 5,0)$,$a = 5$ así lo conseguimos$a^2 = 25$. También sabemos que el centro es$(0,0)$ porque el centro es el punto medio de los vértices. Todo lo que queda es encontrar$b^2$. Para ello, utilizamos el hecho de que la excentricidad$e = \frac{1}{4}$ que significa

$$e = \dfrac{\mbox{distance from the center to a focus}}{\mbox{distance from the center to a vertex}} = \dfrac{c}{a} = \dfrac{c}{5} = \dfrac{1}{4}\nonumber$$

de la que obtenemos$c = \frac{5}{4}$. Para conseguirlo$b^2$, utilizamos el hecho de que$c = \sqrt{a^2 - b^2}$, así$\frac{5}{4} = \sqrt{25-b^2}$ de lo que obtenemos$b^2 = \frac{375}{16}$. Sustituyendo todos nuestros hallazgos en la ecuación$\frac{(x-h)^2}{a^2} + \frac{(y-k)^2}{b^2} = 1$, arroja nuestra respuesta final$\frac{x^2}{25} + \frac{16y^2}{375}=1$.

Al igual que con las paráolas, las elipses tienen una propiedad reflectante. Si imaginamos que las líneas discontinuas de abajo representan ondas sonoras, entonces las ondas que emanan de un foco se reflejan en la parte superior de la elipse y se dirigen hacia el otro foco.

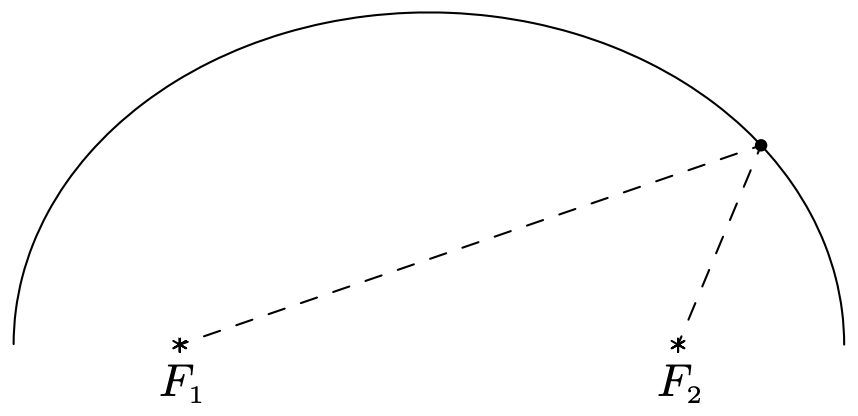
Dicha geometría se explota en la construcción de las llamadas 'Galerías Susurrantes'. Si una persona susurra a un foco, una persona parada en el otro foco escuchará a la primera persona como si estuviera parada justo al lado de ella. Exploramos las Galerías Susurrantes en nuestro último ejemplo.

Ejemplo 7.4.5

Jamie y Jason quieren intercambiar secretos (terribles secretos) desde el otro lado de una concurrida galería de susurros. Recordemos que una galería susurrante es una habitación que, en sección transversal, es la mitad de una elipse. Si la habitación tiene 40 pies de altura en el centro y 100 pies de ancho en el piso, ¿a qué distancia de la pared exterior debe pararse cada una de ellas para que se coloquen en los focos de la elipse?

Solución

Graficando los rendimientos de los datos

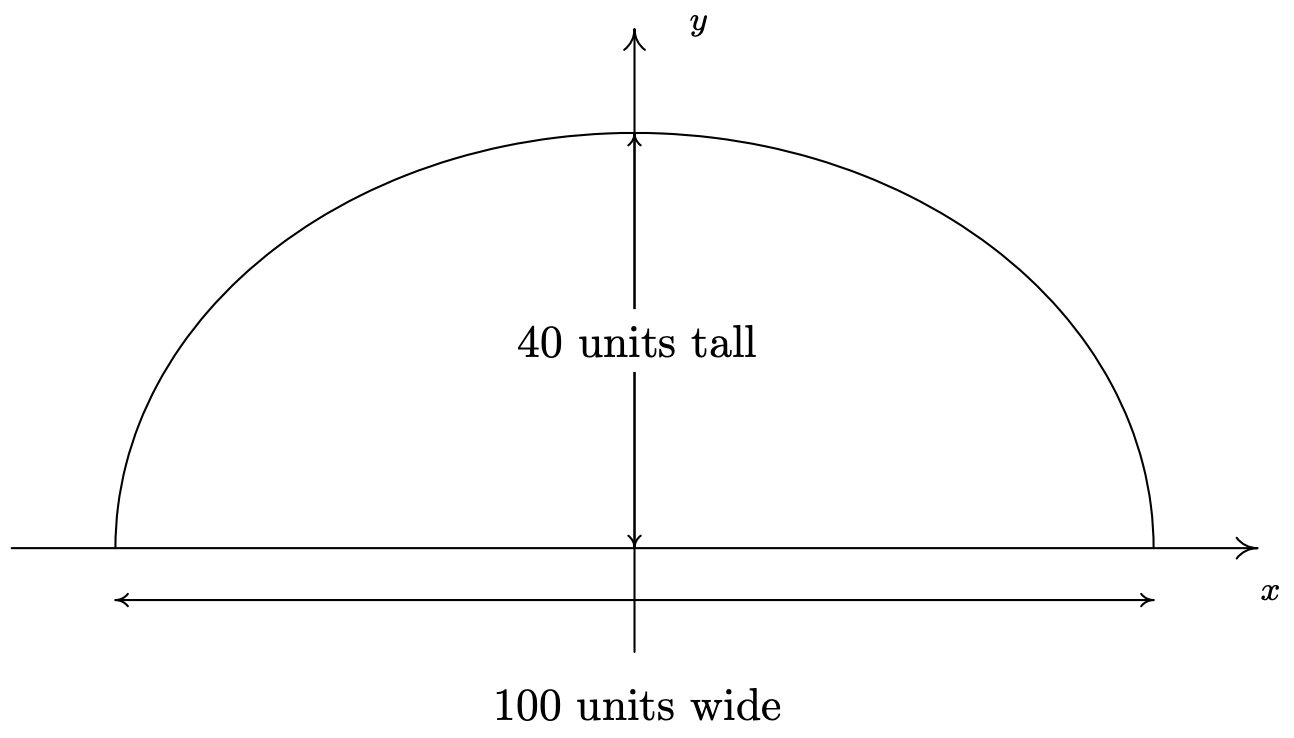
Lo más conveniente es imaginar esta elipse centrada en$(0,0)$. Dado que la elipse es$100$ unidades de ancho y$40$ unidades de alto, obtenemos$a=50$ y$b=40$. De ahí que nuestra elipse tenga la ecuación$\frac{x^2}{50^2}+\frac{y^2}{40^2} = 1$. Estamos buscando los focos, y obtenemos$c = \sqrt{50^2-40^2} = \sqrt{900} = 30$, para que los focos sean$30$ unidades del centro. Eso quiere decir que son$50-30=20$ unidades desde los vértices. De ahí que Jason y Jamie deban pararse a$20$ pies de extremos opuestos de la galería.

7.4.1. Ejercicios

En los Ejercicios 1 - 8, grafica la elipse. Encuentra el centro, las líneas que contienen los ejes mayor y menor, los vértices, los extremos del eje menor, los focos y la excentricidad.

1. $\dfrac{x^{2}}{169} + \dfrac{y^{2}}{25} = 1$
2. $\dfrac{x^2}{9} + \dfrac{y^2}{25} = 1$
3. $\dfrac{(x - 2)^{2}}{4} + \dfrac{(y + 3)^{2}}{9} = 1$
4. $\dfrac{(x + 5)^{2}}{16} + \dfrac{(y - 4)^{2}}{1} = 1$
5. $\dfrac{(x - 1)^{2}}{10} + \dfrac{(y - 3)^{2}}{11} = 1$
6. $\dfrac{(x-1)^2}{9}+\dfrac{(y+3)^2}{4} = 1$
7. $\dfrac{(x+2)^2}{16}+\dfrac{(y-5)^2}{20} = 1$
8. $\dfrac{(x-4)^2}{8} + \dfrac{(y-2)^2}{18} = 1$

En los Ejercicios 9 - 14, ponga la ecuación en forma estándar. Encuentra el centro, las líneas que contienen los ejes mayor y menor, los vértices, los extremos del eje menor, los focos y la excentricidad.

9. $9x^2+25y^2-54x-50y-119=0$
10. $12x^{2} + 3y^{2} - 30y + 39 = 0$
11. $5x^{2} + 18y^{2} - 30x + 72y + 27 = 0$
12. $x^2 - 2x + 2y^2 - 12y + 3 = 0$
13. $9x^2 + 4y^2 - 4y - 8 = 0$
14. $6x^2+5y^2-24x+20y+14=0$

En los Ejercicios 15 - 20, encuentra la forma estándar de la ecuación de la elipse que tiene las propiedades dadas.

15. Centro$(3, 7)$, Vértice$(3, 2)$, Enfoque$(3, 3)$
16. Focos$(0, \pm 5)$, Vértices$(0, \pm 8)$.
17. Focos$(\pm 3, 0)$, longitud del Eje Menor$10$
18. Vértices$(3,2)$,$(13,2)$; Extremos del Eje Menor$(8,4)$,$(8,0)$
19. Centro$(5,2)$, vértice$(0,2)$, excentricidad$\frac{1}{2}$
20. Todos los puntos de la elipse están en el Cuadrante IV excepto$(0, -9)$ y$(8, 0)$. (También se podría decir que la elipse es “tangente a los ejes” en esos dos puntos).
21. Repita el Ejemplo 7.4.5 para una galería susurrante de 200 pies de ancho y 75 pies de alto.
22. Se construye un arco elíptico que mide 6 pies de ancho en la base y 9 pies de alto en el medio. Encuentra la altura del arco exactamente a 1 pie de la base del arco. Compara tu resultado con tu respuesta al Ejercicio 21 en la Sección 7.3.
23. La órbita de la Tierra alrededor del sol es una elipse con el sol en un foco y excentricidad$e \approx 0.0167$. La longitud del eje semimajor (es decir, la mitad del eje mayor) se define como unidad$1$ astronómica (AU). A los vértices de la órbita elíptica se les dan nombres especiales: 'afelio' es el vértice más alejado del sol, y 'perihelio' es el vértice más cercano al sol. Encuentra la distancia en AU entre el sol y el afelio y la distancia en AU entre el sol y el perihelio.
24. La gráfica de una elipse falla claramente la Prueba de Línea Vertical, Teorema 1.1, por lo que la ecuación de una elipse no define$y$ como una función de$x$. Sin embargo, al igual que con los círculos y las parabolas horizontales, podemos dividir una elipse en una mitad superior y una mitad inferior, cada una de las cuales$y$ representaría de hecho en función de$x$. Con la ayuda de tus compañeros de clase, usa tu calculadora para graficar las elipses dadas en los Ejercicios 1 - 8 anteriores. ¿Qué dificultades surgen cuando las planchas en la calculadora?
25. Algunos ejemplos famosos de galerías susurrantes incluyen la Catedral de San Pablo en Londres, Inglaterra, el Salón Nacional de Estatuas en Washington, D.C., y el Cincinnati Museum Center. Con la ayuda de tus compañeros de clase, investiga estas galerías susurrantes. ¿Cómo se compara y contrasta el efecto susurrante con el escenario del Ejemplo 7.4.5?
26. Con la ayuda de tus compañeros, investiga la “litotricia extracorpórea por ondas de choque”. Utiliza la propiedad reflectante del elipsoide para disolver los cálculos renales.

RESPUESTAS

1. $\dfrac{x^{2}}{169} + \dfrac{y^{2}}{25} = 1$

   Centrar eje$(0, 0)$
   mayor a lo largo del eje$y = 0$
   menor a lo largo de$x = 0$
   vértices$(13, 0), \, (-13, 0)$
   Puntos finales del eje menor$(0,-5)$,$(0,5)$
   focos$(12, 0), \, (-12, 0)$
   $e = \frac{12}{13}$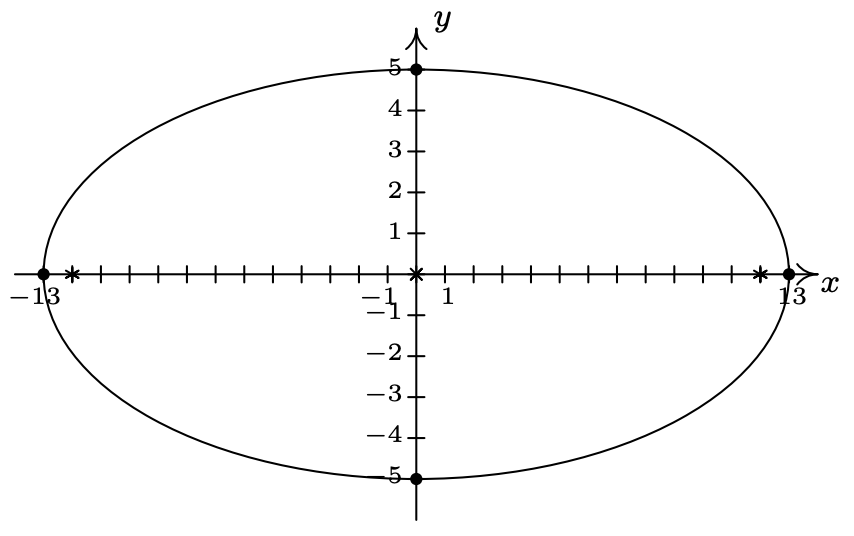

   

2. $\dfrac{x^{2}}{9} + \dfrac{y^{2}}{25} = 1$

   Centrar eje$(0, 0)$
   mayor a lo largo del eje$x = 0$
   menor a lo largo de$y = 0$
   vértices$(0,5), \, (0,-5)$
   Puntos finales del eje menor$(-3,0)$,$(3,0)$
   focos$(0,-4), \, (0,4)$
   $e = \frac{4}{5}$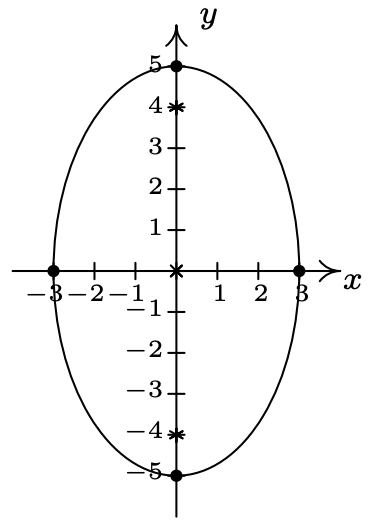

   

3. $\dfrac{(x - 2)^{2}}{4} + \dfrac{(y + 3)^{2}}{9} = 1$

   Centrar eje$(2, -3)$
   mayor a lo largo del eje$x = 2$
   menor a lo largo de$y = -3$
   vértices$(2, 0), \, (2, -6)$
   Puntos finales del eje menor$(0,-3)$,$(4,-3)$
   focos$(2, -3 + \sqrt{5}), \, (2, -3 - \sqrt{5})$
   $e = \frac{\sqrt{5}}{3}$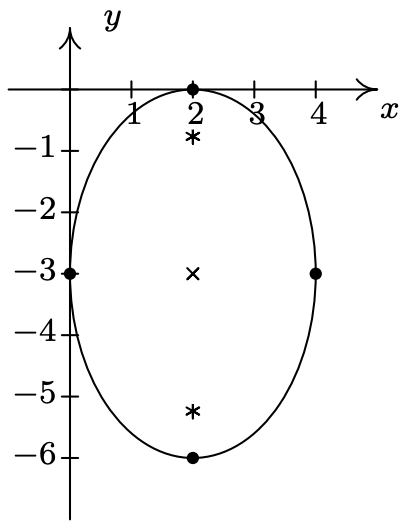

   

4. $\dfrac{(x + 5)^{2}}{16} + \dfrac{(y - 4)^{2}}{1} = 1$

   Centrar eje$(-5, 4)$
   mayor a lo largo del eje$y = 4$
   menor a lo largo de$x = -5$
   vértices$(-9, 4), \, (-1, 4)$
   Puntos finales del eje menor$(-5,3)$,$(-5,5)$
   focos$(-5 + \sqrt{15}, 4), \, (-5 - \sqrt{15}, 4)$
   $e = \frac{\sqrt{15}}{4}$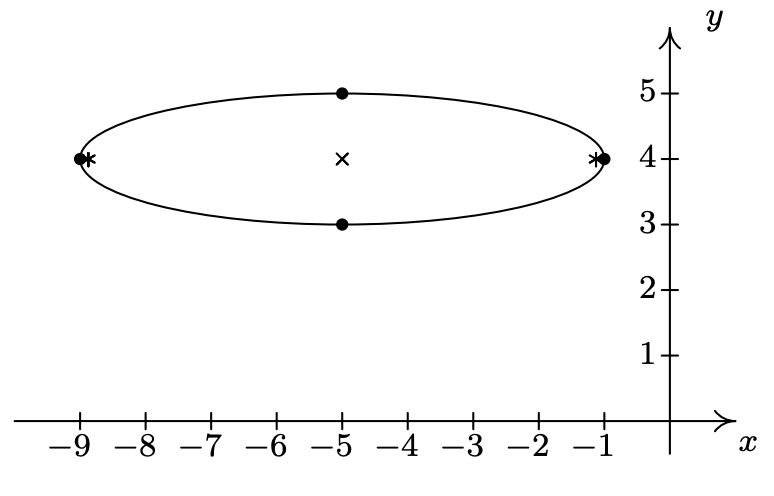

   

5. $\dfrac{(x - 1)^{2}}{10} + \dfrac{(y - 3)^{2}}{11} = 1$

   Centrar eje$(1, 3)$
   mayor a lo largo del eje$x = 1$
   menor a lo largo de$y = 3$
   vértices$(1, 3 + \sqrt{11}), \, (1, 3 - \sqrt{11})$
   Puntos finales de los
   $(1-\sqrt{10}, 3), \, (1+\sqrt{10}, 3)$
   focos del eje menor$(1, 2), \, (1, 4)$
   $e = \frac{\sqrt{11}}{11}$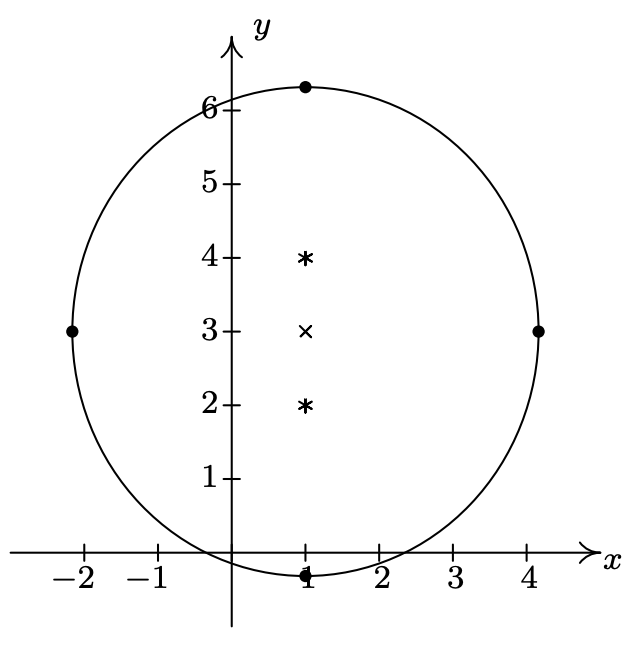

   

6. $\dfrac{(x-1)^2}{9}+\dfrac{(y+3)^2}{4} = 1$

   Centrar el eje$(1, -3)$
   mayor a lo largo del eje$y = -3$
   menor a lo largo de$(4, -3), \, (-2, -3)$
   los$x = 1$
   vértices Puntos finales del eje menor$(1,-1)$,$(1,-5)$
   focos$(1+\sqrt{5}, -3), \, (1-\sqrt{5}, -3)$
   $e = \frac{\sqrt{5}}{3}$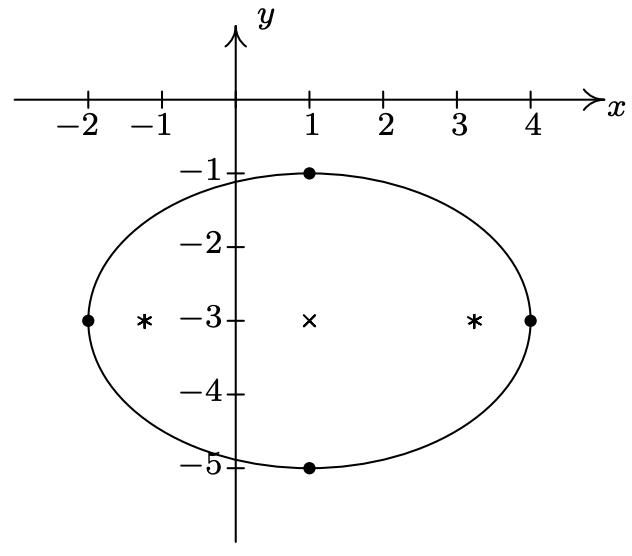

   

7. $\dfrac{(x+2)^2}{16}+\dfrac{(y-5)^2}{20} = 1$

   Centrar el eje$(-2, 5)$
   mayor a lo largo del eje$x = -2$
   menor a lo largo de$(-2, 5 + 2\sqrt{5}), \, (-2, 5 - 2\sqrt{5})$
   los$y = 5$
   vértices Puntos finales del eje menor$(-6,5)$,$(2,5)$ focos$(-2, 7), \, (-2, 3)$
   $e = \frac{\sqrt{5}}{5}$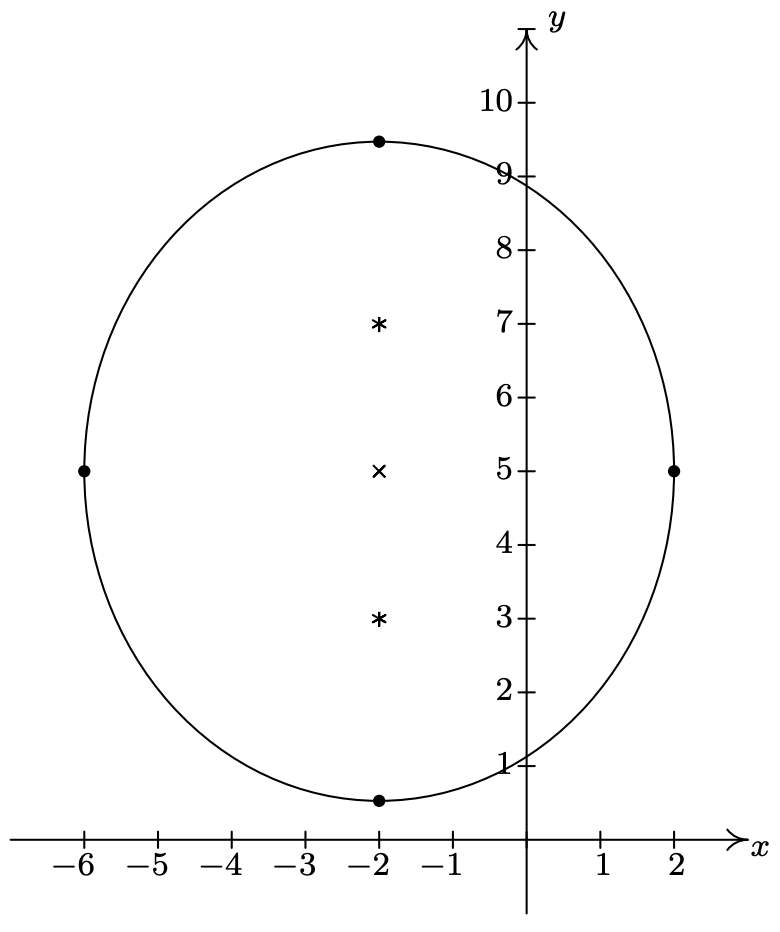

   

8. $\dfrac{(x-4)^2}{8}+\dfrac{(y-2)^2}{18} = 1$

   Centrar el eje$(4, 2)$
   mayor a lo largo del eje$x = 4$
   menor a lo largo de$(4, 2 + 3\sqrt{2}), \, (4, 2 - 3\sqrt{2})$
   los$y = 2$
   vértices Puntos finales del eje menor
   $(4-2\sqrt{2},2)$,$(4+2\sqrt{2},2)$
   focos$(4, 2+\sqrt{10}), \, (4, 2-\sqrt{10})$
   $e = \frac{\sqrt{5}}{3}$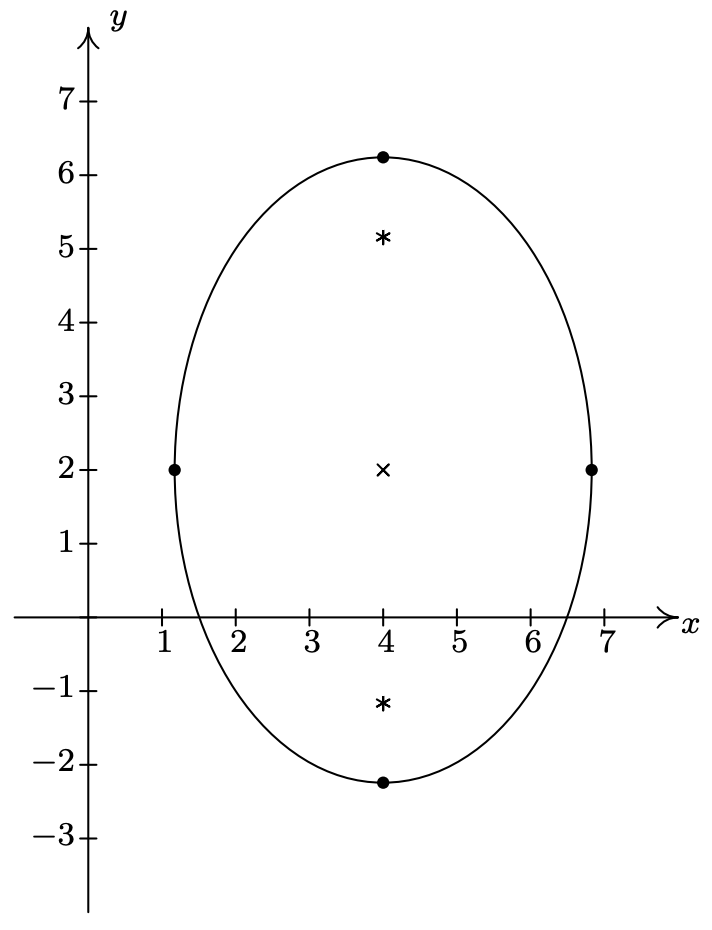

   

9. $\dfrac{(x-3)^2}{25} + \dfrac{\left(y-1\right)^2}{9} = 1$
   Centrar el eje$\left(3, 1 \right)$
   mayor a lo largo del eje$y=1$
   menor a lo largo de$(-2, 1)$
   los$x=3$
   vértices$\left( 8, 1 \right)$, puntos finales del eje menor$\left(3,4\right)$$\left(7,1 \right)$,$\left(3,-2\right)$
   focos, $\left(-1, 1\right)$
   $e = \frac{4}{5}$

10. $\dfrac{x^{2}}{3} + \dfrac{(y - 5)^{2}}{12} = 1$
    Centrar eje$(0, 5)$
    mayor a lo largo del eje$x = 0$
    menor a lo largo de$y = 5$
    vértices$(0, 5 - 2\sqrt{3}), (0, 5 + 2\sqrt{3})$
    Puntos finales del eje menor$(-\sqrt{3},5)$,$(\sqrt{3},5)$
    focos$(0, 2), (0, 8)$
    $e = \frac{\sqrt{3}}{2}$

11. $\dfrac{(x - 3)^{2}}{18} + \dfrac{(y + 2)^{2}}{5} = 1$
    Centrar eje$(3, -2)$
    mayor a lo largo del eje$y = -2$
    menor a lo largo de$x = 3$
    vértices$(3 - 3\sqrt{2}, -2), (3 + 3\sqrt{2}, -2)$
    Puntos finales del eje menor$(3,-2+\sqrt{5})$,$(3,-2-\sqrt{5})$
    focos$(3 - \sqrt{13}, -2), (3 + \sqrt{13}, -2)$
    $e = \frac{\sqrt{26}}{6}$

12. $\dfrac{(x - 1)^{2}}{16} + \dfrac{(y - 3)^{2}}{8} = 1$
    Centrar el eje$(1,3)$
    mayor a lo largo del eje$y=3$
    menor a lo largo de$(-3,3)$
    los$x=1$
    vértices$(5, 3)$, puntos finales del eje menor$(1,3+2\sqrt{2})$$(1 + 2 \sqrt{2}, 3)$,$(1,3-2\sqrt{2})$
    focos, $(1-2 \sqrt{2},3)$
    $e = \frac{\sqrt{2}}{2}$

13. $\dfrac{x^2}{1} + \dfrac{4\left(y-\frac{1}{2}\right)^2}{9} = 1$
    Centrar el eje$\left(0, \frac{1}{2} \right)$
    mayor a lo largo$y$ de$x=0$ (el eje) Eje
    menor a lo largo de$y=\frac{1}{2}$
    los vértices$\left( 0, 2 \right)$,$(0, -1)$
    puntos finales del eje menor$\left(-1, \frac{1}{2} \right)$,$\left(1, \frac{1}{2} \right)$
    Focos$\left(0, \frac{1+\sqrt{5}}{2}\right)$,$\left(0, \frac{1-\sqrt{5}}{2}\right)$
    $e = \frac{\sqrt{5}}{3}$

14. $\dfrac{(x-2)^2}{5} + \dfrac{\left(y+2\right)^2}{6} = 1$
    Centrar el eje$\left(2, -2 \right)$
    mayor a lo largo del eje$x=2$
    menor a lo largo de$(2, -2-\sqrt{6})$
    los$y=-2$
    vértices$\left( 2, -2+\sqrt{6} \right)$, puntos finales del eje menor$\left(2-\sqrt{5},-2 \right)$$\left(2,-1 \right)$,$\left(2+\sqrt{5},-2\right)$
    focos, $\left(2, -3\right)$
    $e = \frac{\sqrt{6}}{6}$

15. $\dfrac{(x - 3)^{2}}{9} + \dfrac{(y - 7)^{2}}{25} = 1$
16. $\dfrac{x^{2}}{39} + \dfrac{y^{2}}{64} = 1$
17. $\dfrac{x^{2}}{34} + \dfrac{y^{2}}{25} = 1$
18. $\dfrac{(x - 8)^{2}}{25} + \dfrac{(y - 2)^{2}}{4} = 1$
19. $\dfrac{(x-5)^{2}}{25} + \dfrac{4(y-2)^{2}}{75} = 1$
20. $\dfrac{(x - 8)^{2}}{64} + \dfrac{(y + 9)^{2}}{81} = 1$
21. Jamie y Jason deberían pararse a$100-25\sqrt{7} \approx 33.86$ pies de extremos opuestos de la galería.
22. El arco puede ser modelado por la mitad superior de$\frac{x^2}{9} + \frac{y^2}{81} = 1$. Un pie adentro de la base del arco corresponde a cualquiera de ellos$x = \pm 2$. El enchufar$x = \pm 2$ da$y = \pm 3\sqrt{5}$ y ya que$y$ representa una altura, elegimos$y=3\sqrt{5} \approx 6.71$ pies.

23. Distancia del sol al afelio$\approx 1.0167$ AU.
    Distancia del sol al perihelio$\approx 0.9833$ AU.

Referencia

¹ Esto fue presagiado en el Ejercicio 19 de la Sección 7.2.

² La ecuación de una parábola tiene solo una variable cuadrada y la ecuación de un círculo tiene dos variables cuadradas con coeficientes idénticos.