7.3: Parábolas
- Page ID
- 119458
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Ya hemos aprendido que la gráfica de una función cuadrática\(f(x) = ax^2 + bx + c\) (\(a \neq 0\)) se llama parábola. Para nuestra sorpresa y deleite, también podemos definir parábolas en términos de distancia.
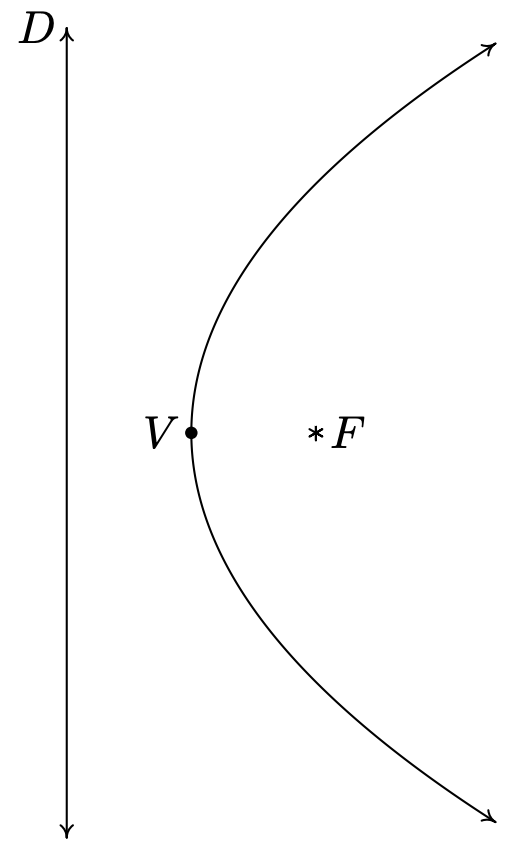
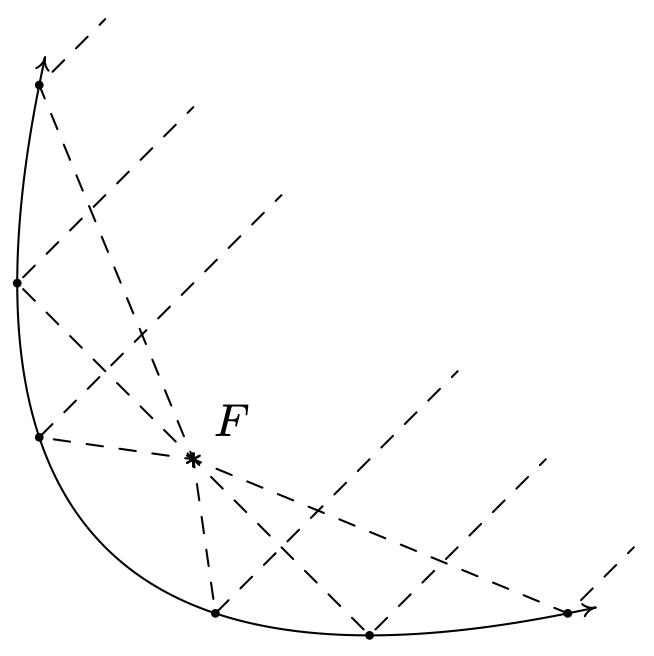
Dejar\(F\) ser un punto en el plano y\(D\) ser una línea que no contenga\(F\). Una parábola es el conjunto de todos los puntos equidistantes de\(F\) y\(D\). Al punto\(F\) se le llama foco de la parábola y a la línea\(D\) se le llama directrix de la parábola.
Esquemáticamente, tenemos lo siguiente.
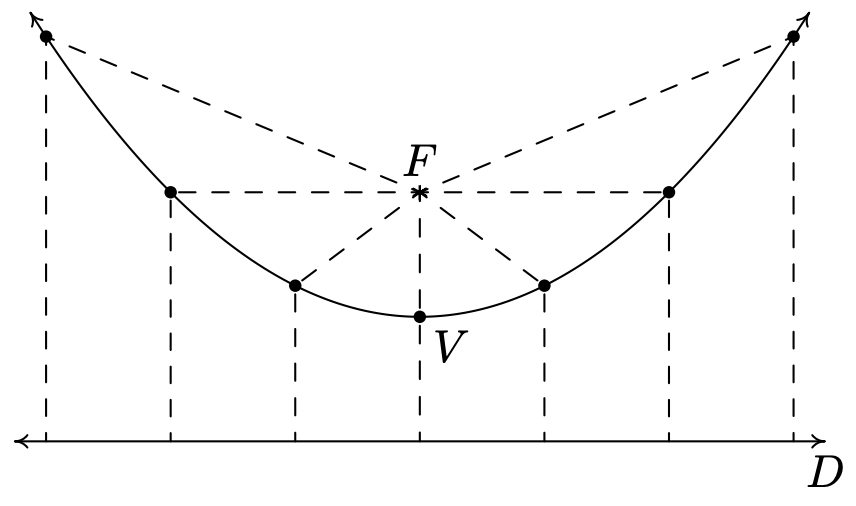
Cada línea discontinua desde el punto\(F\) hasta un punto de la curva tiene la misma longitud que la línea discontinua desde el punto de la curva hasta la línea\(D\). El punto sugestivamente etiquetado\(V\) es, como es de esperar, el vértice. El vértice es el punto en la parábola más cercano al foco.
Queremos utilizar únicamente la definición de distancia de parábola para derivar la ecuación de una parábola y, si todo va bien con el universo, deberíamos obtener una expresión muy parecida a las estudiadas en la Sección 2.3. Dejar\(p\) denotar la distancia dirigida 1 desde el vértice hasta el foco, que por definición es la misma que la distancia desde el vértice a la directrix. Por simplicidad, supongamos que el vértice es\((0,0)\) y que la parábola se abre hacia arriba. De ahí que el foco sea\((0,p)\) y la directrix es la línea\(y = -p\). Nuestro cuadro se convierte en
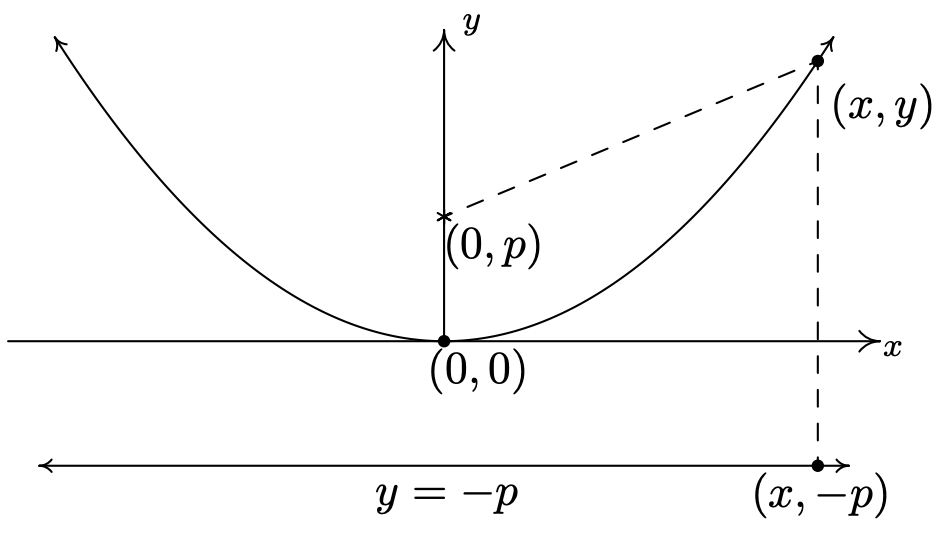
De la definición de parábola, sabemos que la distancia de\((0,p)\) a\((x,y)\) es la misma que la distancia de\((x,-p)\) a\((x,y)\). Usando la Fórmula de Distancia, Ecuación 1.1, obtenemos
\[\begin{array}{rclr} \sqrt{(x -0)^2 + (y-p)^2} & = & \sqrt{(x-x)^2 + (y - (-p))^2} & \\ \sqrt{x^2 + (y-p)^2} & = & \sqrt{(y+p)^2} & \\ x^2 + (y-p)^2 & = & (y+p)^2 & \mbox{square both sides} \\ x^2 + y^2 - 2py + p^2 & = & y^2 + 2py + p^2 & \mbox{expand quantities} \\ x^2 & = & 4py & \mbox{gather like terms} \\ \end{array}\nonumber\]
Resolviendo para\(y\) rendimientos\(y = \frac{x^2}{4p}\), que es una función cuadrática de la forma que se encuentra en la Ecuación 2.4 con\(a = \frac{1}{4p}\) y vértice\((0, 0)\).
Sabemos por experiencia previa que si el coeficiente de\(x^2\) es negativo, la parábola se abre hacia abajo. En la ecuación\(y = \frac{x^2}{4p}\) esto sucede cuando\(p < 0\). En nuestra formulación, decimos que\(p\) es una 'distancia dirigida' desde el vértice hasta el foco: si\(p > 0\), el foco está por encima del vértice; si\(p < 0\), el foco está por debajo del vértice. La distancia focal de una parábola es\(|p|\).
Si elegimos colocar el vértice en un punto arbitrario\((h,k)\), llegamos a la siguiente fórmula usando transformaciones de la Sección 1.7 o volviendo a derivar la fórmula de la Definición 7.3.
La ecuación de una parábola (vertical) con vértice\((h,k)\) y distancia focal\(|p|\) es
\[(x-h)^2 = 4p(y-k)\nonumber\]
Si\(p>0\), la parábola se abre hacia arriba; si\(p < 0\), se abre hacia abajo.
a Es decir, una parábola que se abre ya sea hacia arriba o hacia abajo.
Observe que en la ecuación estándar de la parábola anterior, sólo una de las variables\(x\),, es cuadrada. Esta es una manera rápida de distinguir una ecuación de una parábola de la de un círculo porque en la ecuación de un círculo, ambas variables son cuadradas.
Gráfica\((x+1)^2 = -8(y-3)\). Encuentra el vértice, el enfoque y la directrix.
Solución
Reconocemos esto como la forma dada en la Ecuación 7.2. Aquí,\(x-h\) es\(x+1\) así\(h = -1\), y\(y-k\) es\(y-3\) así\(k = 3\). De ahí que el vértice sea\((-1,3)\). También vemos eso\(4p = -8\) así\(p = -2\). Ya que\(p < 0\), el foco estará por debajo del vértice y la parábola se abrirá hacia abajo.
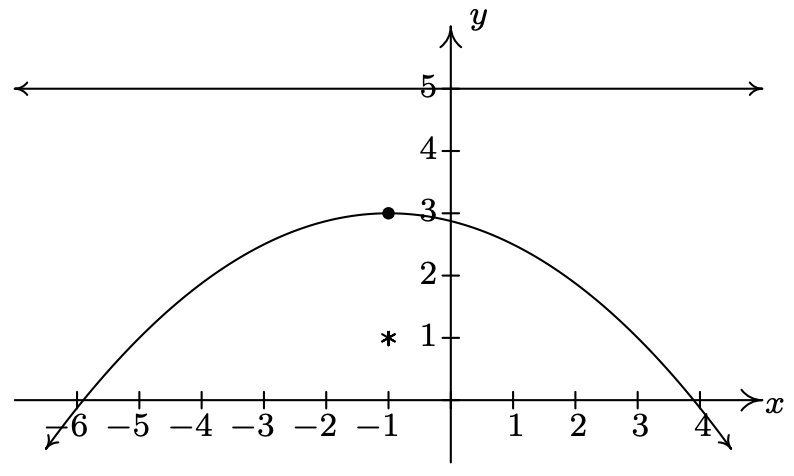
La distancia desde el vértice hasta el foco es\(|p| = 2\), lo que significa que el foco es\(2\) unidades por debajo del vértice. De\((-1,3)\), bajamos\(2\) unidades y encontramos el foco en\((-1,1)\). La directrix, entonces, es\(2\) unidades por encima del vértice, por lo que es la línea\(y=5\).
De toda la información solicitada en el ejemplo anterior, sólo el vértice forma parte de la gráfica de la parábola. Entonces, para tener una idea de la forma real de la gráfica, necesitamos algo más de información. Si bien podríamos trazar algunos puntos al azar, una medida más útil de lo ancho que se abre una parábola es la longitud del recto latus de la parábola. 2 El recto latus de una parábola es el segmento lineal paralelo a la directrix que contiene el foco. Los puntos finales del recto latus son, entonces, dos puntos en lados 'opuestos' de la parábola. Gráficamente, tenemos lo siguiente.
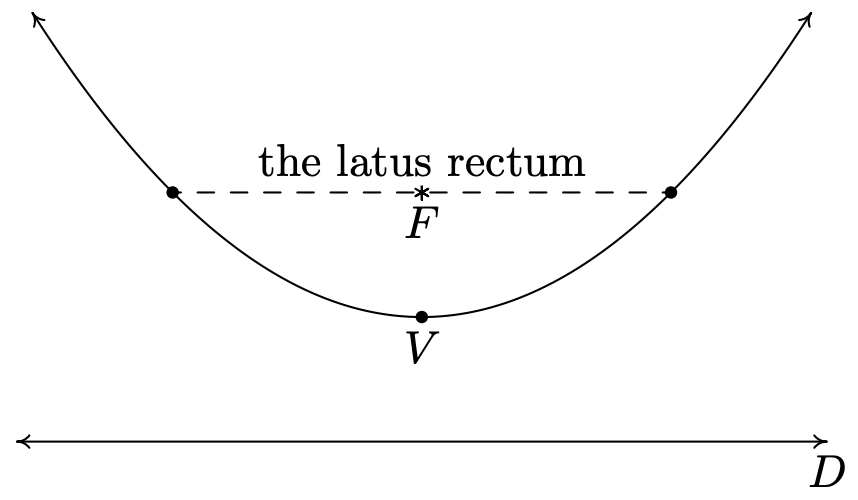
Resulta 3 que es la longitud del recto latus, llamado diámetro focal de la parábola\(|4p|\), que, a la luz de la Ecuación 7.2, es fácil de encontrar. En nuestro último ejemplo, por ejemplo, al graficar\((x+1)^2 = -8(y-3)\), podemos usar el hecho de que el diámetro focal es\(|-8| = 8\), lo que significa que la parábola es de\(8\) unidades de ancho en el foco, para ayudar a generar una gráfica más precisa trazando\(4\) unidades de puntos a la izquierda y derecha del foco.
Encuentra la forma estándar de la parábola con enfoque\((2,1)\) y directrix\(y = -4\).
Solución
Dibujando los rendimientos de los datos,
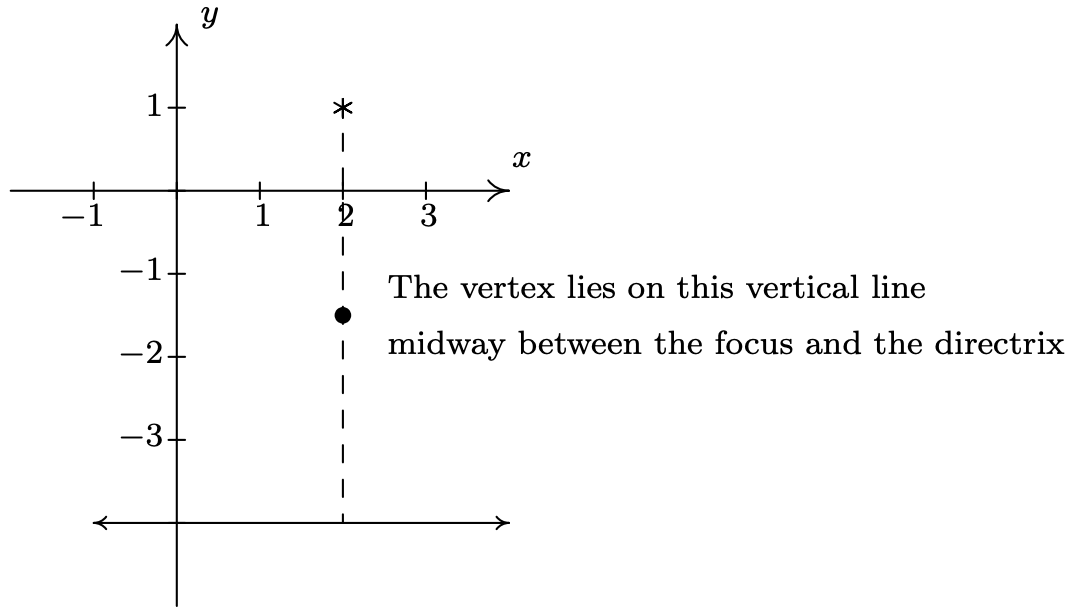
Del diagrama, vemos que la parábola se abre hacia arriba. (Tómate un momento para pensarlo si no lo ves de inmediato). De ahí que el vértice se encuentre por debajo del foco y tenga una\(x\) coordenada de\(2\). Para encontrar la\(y\) coordenada -observamos que la distancia desde el foco a la directrix es\(1 - (-4) = 5\), lo que significa que el vértice se encuentra\(\frac{5}{2}\) unidades (a mitad de camino) debajo del foco. Empezar en\((2,1)\) y bajar\(5/2\) unidades nos deja en\((2, -3/2)\), que es nuestro vértice. Ya que la parábola se abre hacia arriba, sabemos que\(p\) es positiva. Así\(p = 5/2\). La conexión de todos estos datos en la Ecuación 7.2 nos da
\[\begin{array}{rclr} (x-2)^2 & = & 4 \left(\dfrac{5}{2}\right) \left(y - \left(-\dfrac{3}{2}\right)\right) & \\ (x-2)^2 & = & 10\left(y + \dfrac{3}{2}\right) & \\ \end{array}\nonumber\]
Si cambiamos los roles de\(x\) y\(y\), podemos producir paráolas 'horizontales': parácharas que se abren a la izquierda o a la derecha. Las pautas 4 de tales animales serían líneas verticales y el foco estaría bien a la izquierda o a la derecha del vértice, como se ve a continuación.
La ecuación de una parábola (horizontal) con vértice\((h,k)\) y distancia focal\(|p|\) es
\[(y-k)^2 = 4p(x-h)\nonumber\]
Si\(p>0\), la parábola se abre a la derecha; si\(p < 0\), se abre a la izquierda.
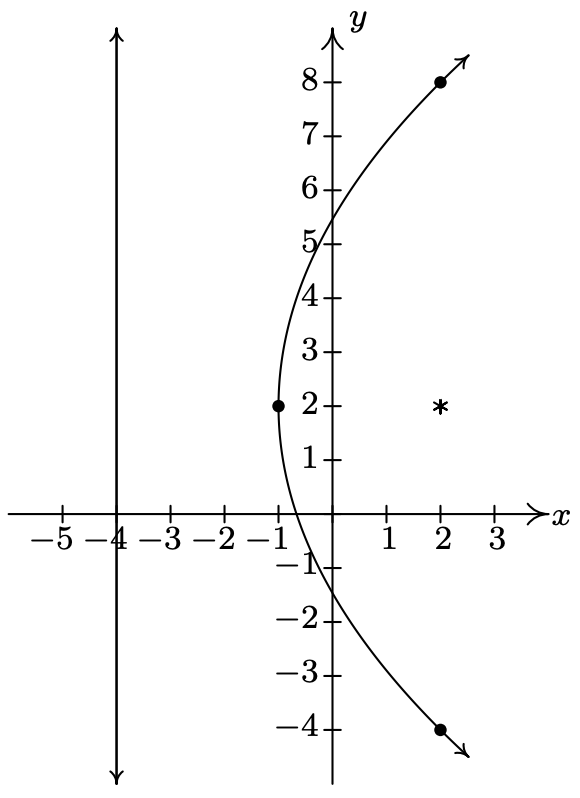
Gráfica\((y-2)^2 = 12(x+1)\). Encuentra el vértice, el enfoque y la directrix.
Solución
Reconocemos esto como la forma dada en la Ecuación 7.3. Aquí,\(x-h\) es\(x+1\) así\(h = -1\), y\(y-k\) es\(y-2\) así\(k = 2\). De ahí que el vértice sea\((-1,2)\). También vemos eso\(4p = 12\) así\(p = 3\). Ya que\(p > 0\), el foco será el derecho del vértice y la parábola se abrirá a la derecha. La distancia desde el vértice hasta el foco es\(|p| = 3\), lo que significa que el foco es\(3\) unidades a la derecha. Si empezamos en\((-1,2)\) y movemos\(3\) las unidades correctas, llegamos al foco\((2,2)\). La directrix, entonces, es\(3\) unidades a la izquierda del vértice y si movemos\(3\) las unidades de la izquierda\((-1,2)\), estaríamos en la línea vertical\(x=-4\). Dado que el diámetro focal es\(|4p| = 12\), la parábola es\(12\) unidades de ancho en el foco, y así hay\(6\) unidades de puntos por encima y por debajo del foco en la parábola.
Al igual que con los círculos, no todas las parábolas nos llegarán en las formas de las Ecuaciones 7.2 o 7.3. Si encontramos una ecuación con dos variables en las que exactamente una variable es cuadrada, podemos intentar poner la ecuación en una forma estándar usando los siguientes pasos.
- Agrupe la variable que está cuadrada en un lado de la ecuación y posicione la variable no cuadrada y la constante en el otro lado.
- Completa el cuadrado si es necesario y divide por el coeficiente del cuadrado perfecto.
- Factorizar el coeficiente de la variable no cuadrada de éste y la constante.
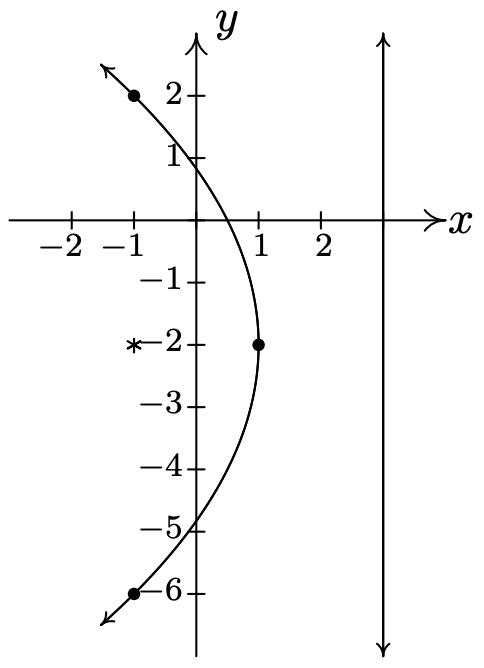
Considera la ecuación\(y^2 + 4y + 8x = 4\). Pon esta ecuación en forma estándar y grafica la parábola. Encuentra el vértice, el enfoque y la directrix.
Solución
Necesitamos un cuadrado perfecto (en este caso, usando\(y\)) en el lado izquierdo de la ecuación y factorizar el coeficiente de la variable no cuadrada (en este caso, la\(x\)) en el otro.
\[\begin{array}{rclr} y^2+4y+8x & = & 4 & \\ y^2 + 4y & = & -8x + 4 & \\ y^2+4y+4 & = & -8x+4+4 & \mbox{complete the square in $y$ only} \\ (y+2)^2 & = &-8x+8 & \mbox{factor} \\ (y+2)^2 & = & -8(x-1) & \end{array}\nonumber\]
Ahora que la ecuación está en la forma dada en la Ecuación 7.3, vemos que\(x-h\) es\(x-1\) así\(h = 1\), y\(y-k\) es\(y+2\) así\(k = -2\). De ahí que el vértice sea\((1,-2)\). También vemos eso\(4p = -8\) para que\(p = -2\). Ya que\(p < 0\), el foco será la izquierda del vértice y la parábola se abrirá hacia la izquierda. La distancia desde el vértice hasta el foco es\(|p| = 2\), lo que significa que el foco es\(2\) unidades a la izquierda de\(1\), así que si empezamos en\((1,-2)\) y movemos\(2\) las unidades a la izquierda, llegamos al foco\((-1,-2)\). La directrix, entonces, es\(2\) unidades a la derecha del vértice, así que si movemos\(2\) las unidades derechas de\((1,-2)\), estaríamos en la línea vertical\(x=3\). Dado que el diámetro focal es\(|4p|\) es\(8\), la parábola es\(8\) unidades de ancho en el foco, por lo que hay puntos\(4\) unidades por encima y por debajo del foco en la parábola.
Al estudiar las funciones cuadráticas, hemos visto paráolas utilizadas para modelar fenómenos físicos como las trayectorias de proyectiles. Otras aplicaciones de la parábola se refieren a su 'propiedad reflectante' que requiere conocer el foco de una parábola. Por ejemplo, muchas antenas parabólicas se forman en forma de paraboloide de revolución como se representa a continuación.

Cada sección transversal a través del vértice del paraboloide es una parábola con el mismo enfoque. Para ver por qué esto es importante, imagina las líneas discontinuas de abajo como ondas electromagnéticas que se dirigen hacia un plato parabólico. Resulta que las ondas se reflejan en la parábola y se concentran en el foco que luego se convierte en el lugar óptimo para el receptor. Si, por otro lado, imaginamos las líneas discontinuas como emanadas del foco, vemos que las ondas se reflejan en la parábola de manera coherente como en el caso de una linterna. Aquí, la bombilla se coloca en el foco y los rayos de luz se reflejan en un espejo parabólico para dar luz direccional.
Una antena parabólica se va a construir en forma de paraboloide de revolución. Si el receptor colocado en el foco se encuentra a 2 pies por encima del vértice del plato, y el plato debe tener 12 pies de ancho, ¿qué tan profundo será el plato?
Solución
Una forma de abordar este problema es determinar la ecuación de la parábola que nos sugiere estos datos. Por simplicidad, asumiremos que el vértice es\((0,0)\) and the parabola opens upwards. Our standard form for such a parabola is \(x^2 = 4py\). Since the focus is \(2\) units above the vertex, we know \(p=2\), so we have \(x^2 = 8y\). Visually,
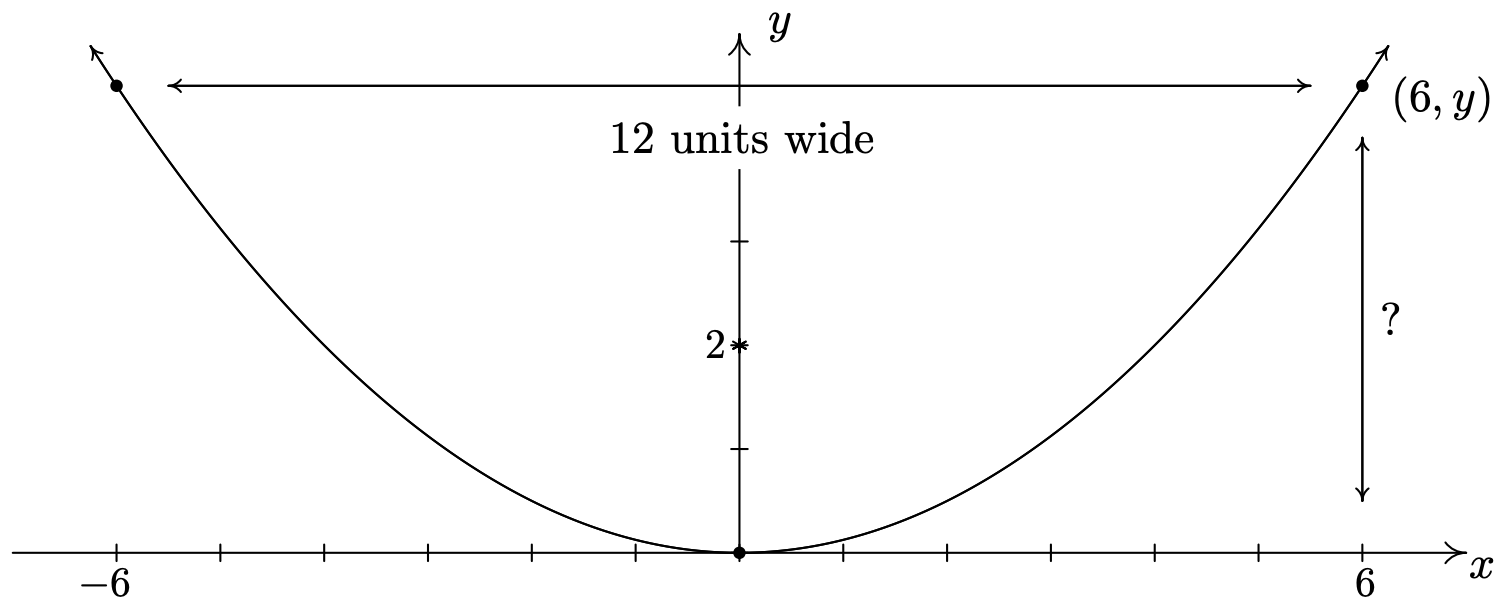
Since the parabola is \(12\) feet wide, we know the edge is \(6\) feet from the vertex. To find the depth, we are looking for the \(y\) value when \(x=6\). Substituting \(x=6\) into the equation of the parabola yields \(6^2 = 8y\) or \(y = \frac{36}{8} = \frac{9}{2} = 4.5\). Hence, the dish will be \(4.5\) feet deep.
7.3.1. Exercises
In Exercises 1 - 8, sketch the graph of the given parabola. Find the vertex, focus and directrix. Include the endpoints of the latus rectum in your sketch.
- \((x - 3)^{2} = -16y\)
- \(\left(x + \frac{7}{3}\right)^{2} = 2\left(y + \frac{5}{2}\right)\)
- \((y - 2)^{2} = -12(x + 3)\)
- \((y + 4)^{2} = 4x\)
- \((x-1)^2 = 4(y+3)\)
- \((x+2)^2 = -20(y-5)\)
- \((y-4)^2 = 18(x-2)\)
- \(\left(y+ \frac{3}{2}\right)^2 = -7 \left(x+ \frac{9}{2}\right)\)
In Exercises 9 - 14, put the equation into standard form and identify the vertex, focus and directrix.
- \(y^{2} - 10y - 27x + 133 = 0\)
- \(25x^{2} + 20x + 5y - 1 = 0\)
- \(x^2 + 2x - 8y + 49 = 0\)
- \(2y^2 + 4y +x - 8 = 0\)
- \(x^2-10x+12y+1=0\)
- \(3y^2-27y+4x+\frac{211}{4} = 0\)
In Exercises 15 - 18, find an equation for the parabola which fits the given criteria.
- Vertex \((7, 0)\), focus \((0, 0)\)
- Focus \((10, 1)\), directrix \(x = 5\)
- Vertex \((-8, -9)\); \((0, 0)\) and \((-16, 0)\) are points on the curve
- The endpoints of latus rectum are \((-2, -7)\) and \((4, -7)\)
- The mirror in Carl’s flashlight is a paraboloid of revolution. If the mirror is 5 centimeters in diameter and 2.5 centimeters deep, where should the light bulb be placed so it is at the focus of the mirror?
- A parabolic Wi-Fi antenna is constructed by taking a flat sheet of metal and bending it into a parabolic shape.5 If the cross section of the antenna is a parabola which is 45 centimeters wide and 25 centimeters deep, where should the receiver be placed to maximize reception?
- [parabolaarch] A parabolic arch is constructed which is 6 feet wide at the base and 9 feet tall in the middle. Find the height of the arch exactly 1 foot in from the base of the arch.
- A popular novelty item is the ‘mirage bowl.’ Follow this link to see another startling application of the reflective property of the parabola.
- With the help of your classmates, research spinning liquid mirrors. To get you started, check out this website.
7.3.2. Answers
-
\((x - 3)^{2} = -16y\)
Vertex \((3, 0)\)
Focus \((3, -4)\)
Directrix \(y = 4\)
Endpoints of latus rectum \((-5, -4)\), \((11, -4)\)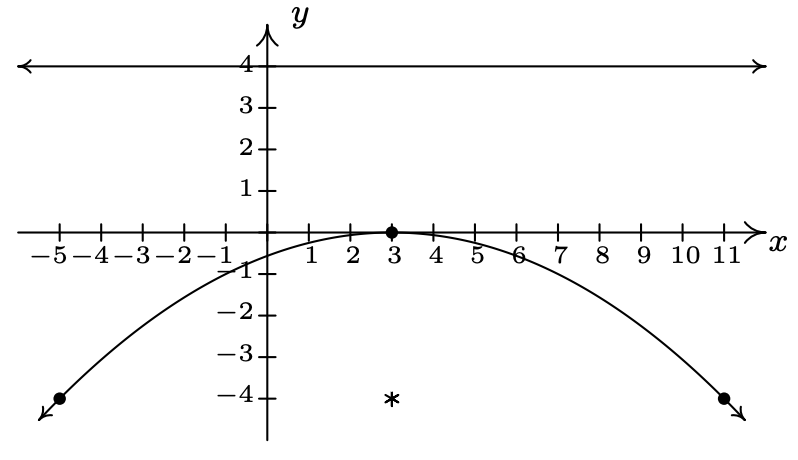
-
\(\left(x + \frac{7}{3}\right)^{2} = 2\left(y + \frac{5}{2}\right)\)
Vertex \(\left(-\frac{7}{3}, -\frac{5}{2} \right)\)
Focus \(\left(-\frac{7}{3}, -2 \right)\)
Directrix \(y = -3\)
Endpoints of latus rectum \(\left(-\frac{10}{3}, -2 \right)\), \(\left(-\frac{4}{3}, -2 \right)\)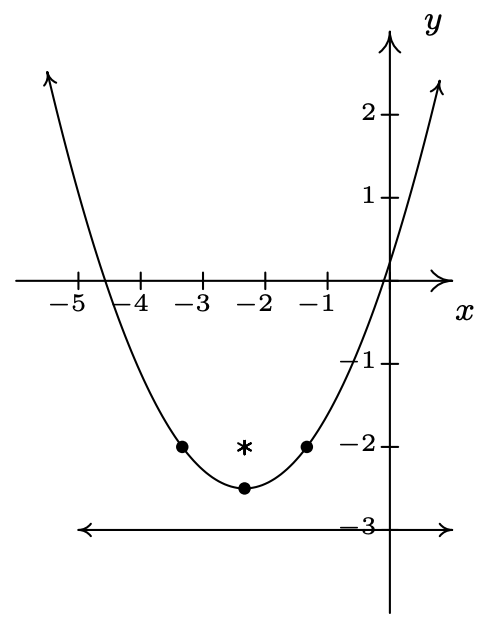
-
\((y - 2)^{2} = -12(x + 3)\)
Vertex \((-3, 2)\)
Focus \((-6, 2)\)
Directrix \(x = 0\)
Endpoints of latus rectum \((-6, 8)\), \((-6, -4)\)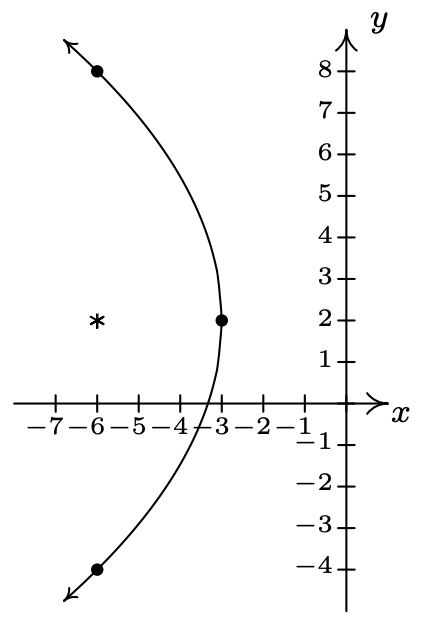
-
\((y + 4)^{2} = 4x\)
Vertex \((0,-4)\)
Focus \((1,-4)\)
Directrix \(x = -1\)
Endpoints of latus rectum \((1, -2)\), \((1, -6)\)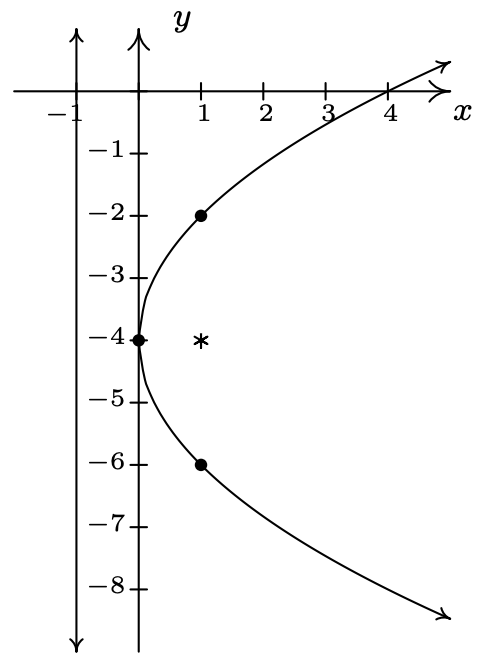
-
\((x-1)^2 = 4(y+3)\)
Vertex \(\left(1, -3\right)\)
Focus \(\left(1, -2 \right)\)
Directrix \(y = -4\)
Endpoints of latus rectum \(\left(3, -2 \right)\), \(\left(-1, -2 \right)\)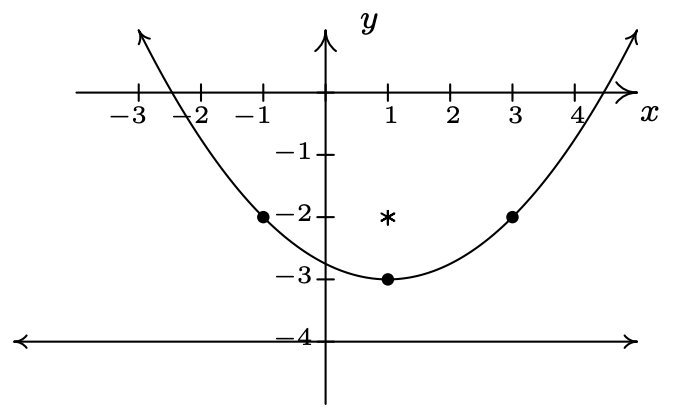
-
\((x+2)^2 = -20(y-5)\)
Vertex \(\left(-2, 5\right)\)
Focus \(\left(-2, 0 \right)\)
Directrix \(y = 10\)
Endpoints of latus rectum \(\left(-12, 0 \right)\), \(\left(8, 0 \right)\)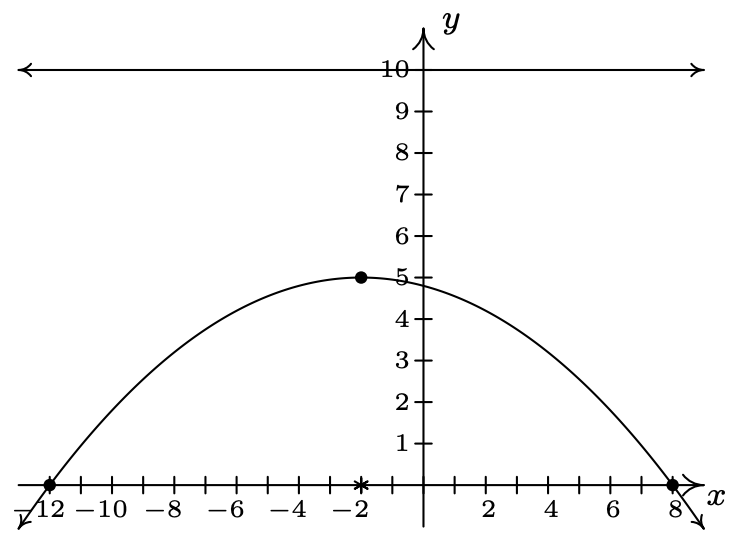
-
\((y-4)^2 = 18(x-2)\)
Vertex \(\left(2, 4\right)\)
Focus \(\left( \frac{13}{2}, 4 \right)\)
Directrix \(x = -\frac{5}{2}\)
Endpoints of latus rectum \(\left(\frac{13}{2}, -5 \right)\), \(\left(\frac{13}{2}, 13 \right)\)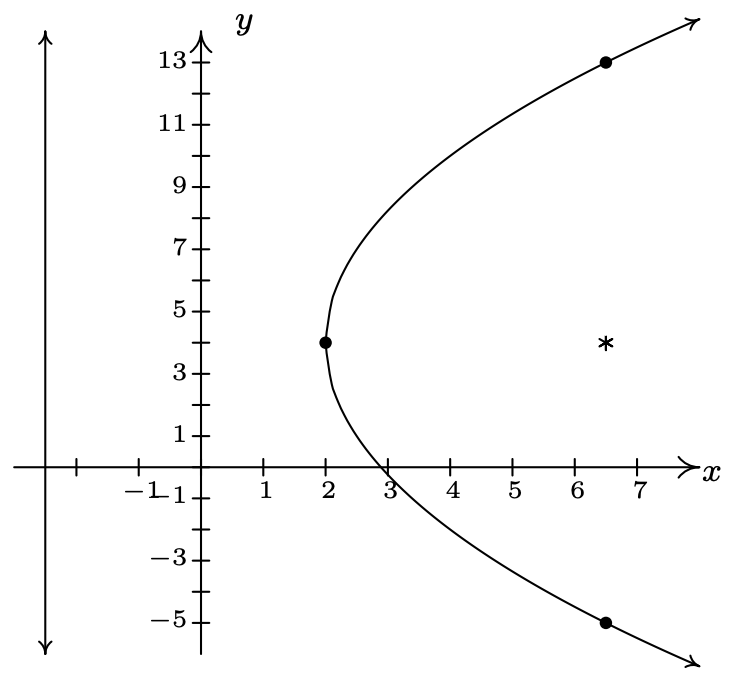
-
\(\left(y+ \frac{3}{2}\right)^2 = -7 \left(x+ \frac{9}{2}\right)\)
Vertex \(\left(-\frac{9}{2}, -\frac{3}{2}\right)\)
Focus \(\left( -\frac{25}{4}, -\frac{3}{2} \right)\)
Directrix \(x = -\frac{11}{4}\)
Endpoints of latus rectum \(\left(-\frac{25}{4}, 2 \right)\), \(\left(-\frac{25}{4}, -5 \right)\)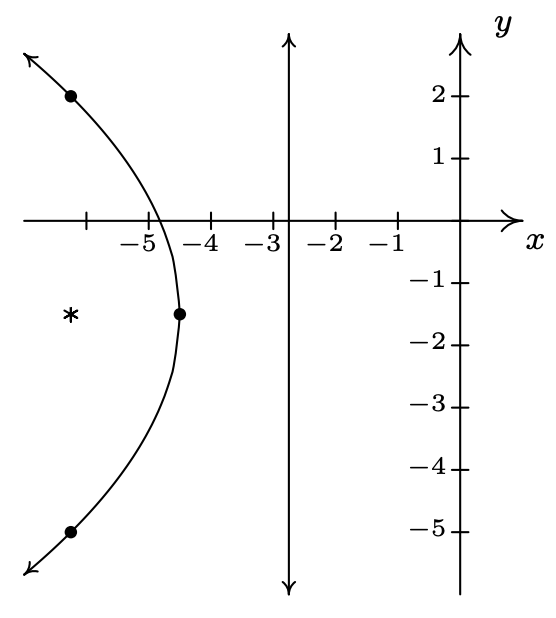
-
\((y - 5)^{2} = 27(x - 4)\)
Vertex \((4, 5)\)
Focus \(\left( \frac{43}{4}, 5 \right)\)
Directrix \(x = -\frac{11}{4}\) -
\(\left(x + \frac{2}{5} \right)^{2} = -\frac{1}{5}(y - 1)\)
Vertex \(\left( -\frac{2}{5}, 1 \right)\)
Focus \(\left( -\frac{2}{5}, \frac{19}{20} \right)\)
Directrix \(y = \frac{21}{20}\) -
\((x+1)^2=8(y-6)\)
Vertex \((-1,6)\)
Focus \((-1,8)\)
Directrix \(y=4\) -
\((y+1)^2=-\frac{1}{2}(x-10)\)
Vertex \((10,-1)\)
Focus \(\left(\frac{79}{8}, -1 \right)\)
Directrix \(x = \frac{81}{8}\) -
\((x-5)^2 = -12(y-2)\)
Vertex \((5,2)\)
Focus \((5,-1)\)
Directrix \(y=5\) -
\(\left(y-\frac{9}{2}\right)^2 = -\frac{4}{3} (x-2)\)
Vertex \(\left(2, \frac{9}{2}\right)\)
Focus \(\left(\frac{5}{3}, \frac{9}{2}\right)\)
Directrix \(x = \frac{7}{3}\) - \(y^{2} = -28(x - 7)\)
- \((y - 1)^{2} = 10\left(x - \frac{15}{2} \right)\)
- \((x + 8)^{2} = \frac{64}{9}(y + 9)\)
-
\((x - 1)^{2} = 6\left(y + \frac{17}{2}\right)\) or
\((x - 1)^{2} = -6\left(y + \frac{11}{2}\right)\) - The bulb should be placed \(0.625\) centimeters above the vertex of the mirror. (As verified by Carl himself!)
- The receiver should be placed \(5.0625\) centimeters from the vertex of the cross section of the antenna.
- The arch can be modeled by \(x^2=-(y-9)\) or \(y=9-x^2\). One foot in from the base of the arch corresponds to either \(x = \pm 2\), so the height is \(y=9-(\pm 2)^2=5\) feet.
Reference
1 We’ll talk more about what ‘directed’ means later.
2 No, I’m not making this up.
3 Consider this an exercise to show what follows.
4 Plural of ‘directrix’
5 This shape is called a 'parabolic cylinder.'


