6.6: Ortogonalidad de Curvas
- Page ID
- 109709
Una propiedad importante de los conjugados armónicos\(u\) y\(v\) es que sus curvas de nivel son ortogonales. Comenzamos mostrando que sus gradientes son ortogonales.
Supongamos que eso\(f(z) = u(x, y) + iv(x, y)\) es analítico.\(z = x + iy\) Entonces el producto de punto de sus gradientes es 0, i.e.
\[\Delta u \cdot \Delta v = 0.\]
- Prueba
-
La prueba es una fácil aplicación de las ecuaciones de Cauchy-Riemann.
\[\Delta u \cdot \Delta v = (u_x, u_y) \cdot (v_x, v_y) = u_x v_x + u_y v_y = v_y v_x - v_x v_y = 0\]
En el último paso utilizamos las ecuaciones de Cauchy-Riemann\(v_y\) para sustituir\(u_x\) y\(-v_x\) para\(u_y\).
El lema sostiene si los gradientes son o no 0. Para garantizar que las curvas de nivel sean suaves el siguiente teorema lo requiere\(f'(z) \ne 0\).
Dejemos\(z = x + iy\) y supongamos que
\[f(z) = u(x, y) + iv(x, y)\]
es analítico. Si\(f'(z) \ne 0\) entonces la curva de nivel de\(u\) through\((x, y)\) es ortogonal a la curva de nivel\(v\) a través\((x, y)\).
- Prueba
-
El requisito técnico que\(f'(z) \ne 0\) se necesita para asegurarse de que las curvas de nivel sean suaves. Necesitamos suavidad para que incluso tenga sentido preguntar si las curvas son ortogonales. Discutiremos esto a continuación. Suponiendo que las curvas son suaves la prueba del teorema es trivial: Sabemos a partir del 18.02 que el gradiente\(\nabla u\) es ortogonal a las curvas de nivel de\(u\) y lo mismo es cierto para\(\nabla v\) y las curvas de nivel de\(v\). Dado que, por Lema 6.6.1, los gradientes son ortogonales esto implica que las curvas son ortogonales.
Finalmente, mostramos que\(f'(z) \ne 0\) significa que las curvas son suaves. Primero tenga en cuenta que
\[f'(z) = u_x(x, y) - iu_y (x, y) = v_y (x, y) + iv_x (x, y).\]
Ahora, ya\(f'(z) \ne 0\) que sabemos que
\[\nabla u = (u_x, u_y) \ne 0.\]
De igual manera,\(\nabla v \ne 0\). Así, los gradientes no son cero y las curvas de nivel deben ser suaves.
Las siguientes figuras muestran curvas de nivel de\(u\) y\(v\) para una serie de funciones. En todos los casos, las curvas de nivel de\(u\) están en naranja y las de\(v\) son en azul. Para cada caso mostramos las curvas de nivel por separado y luego superponiendo unas sobre otras.
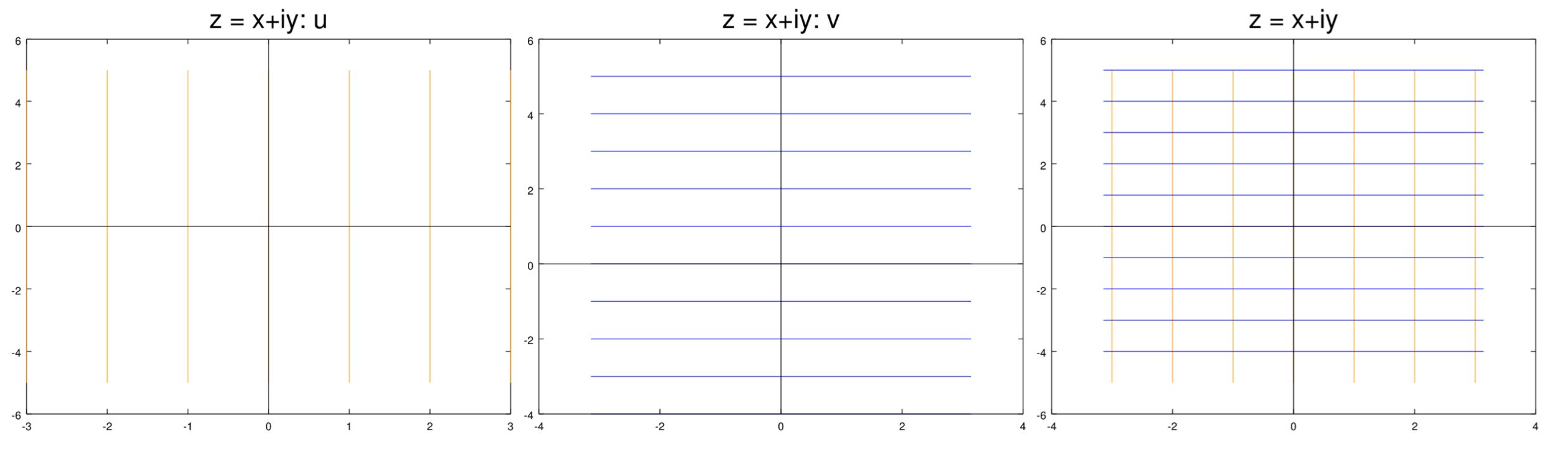
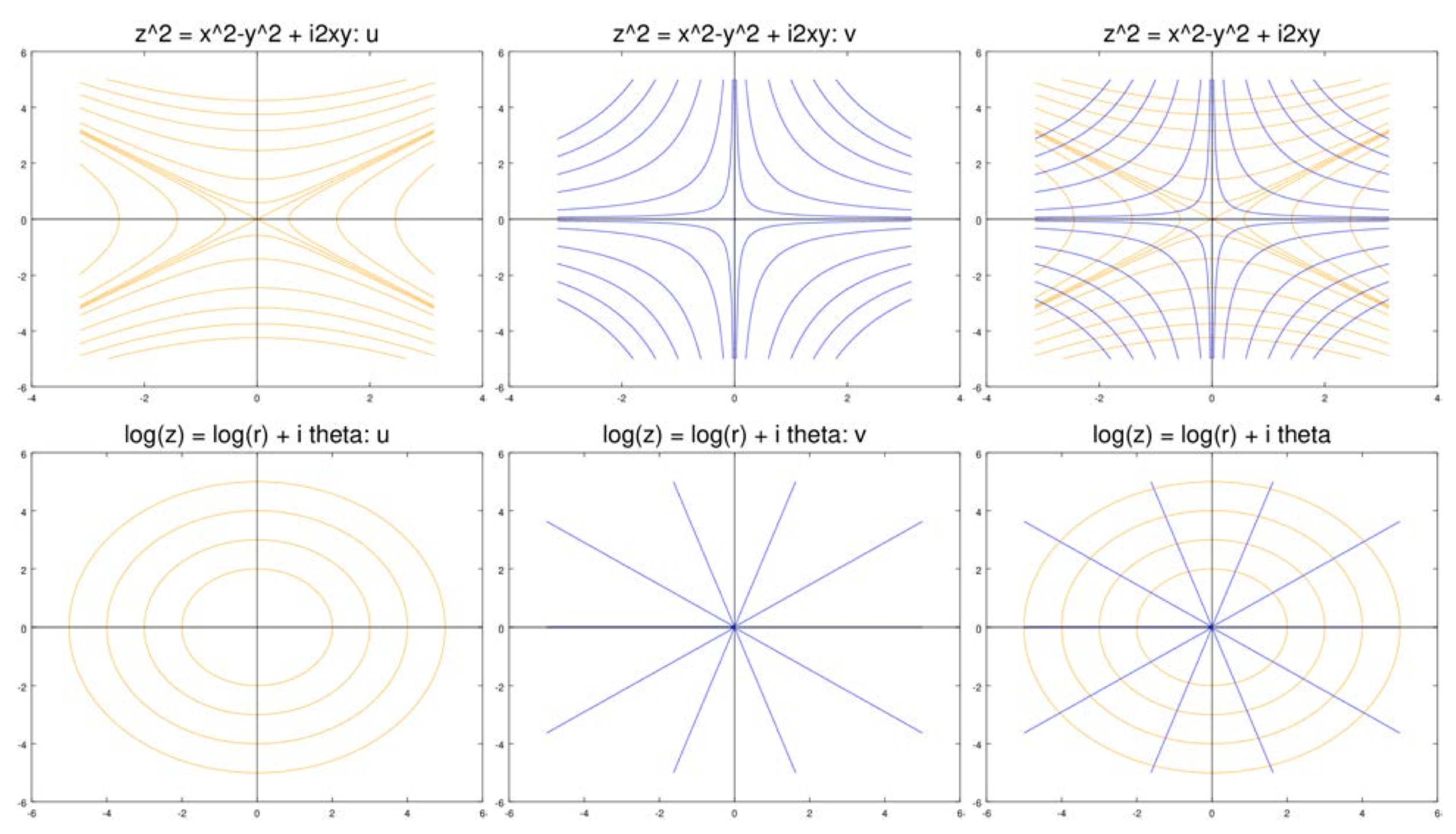
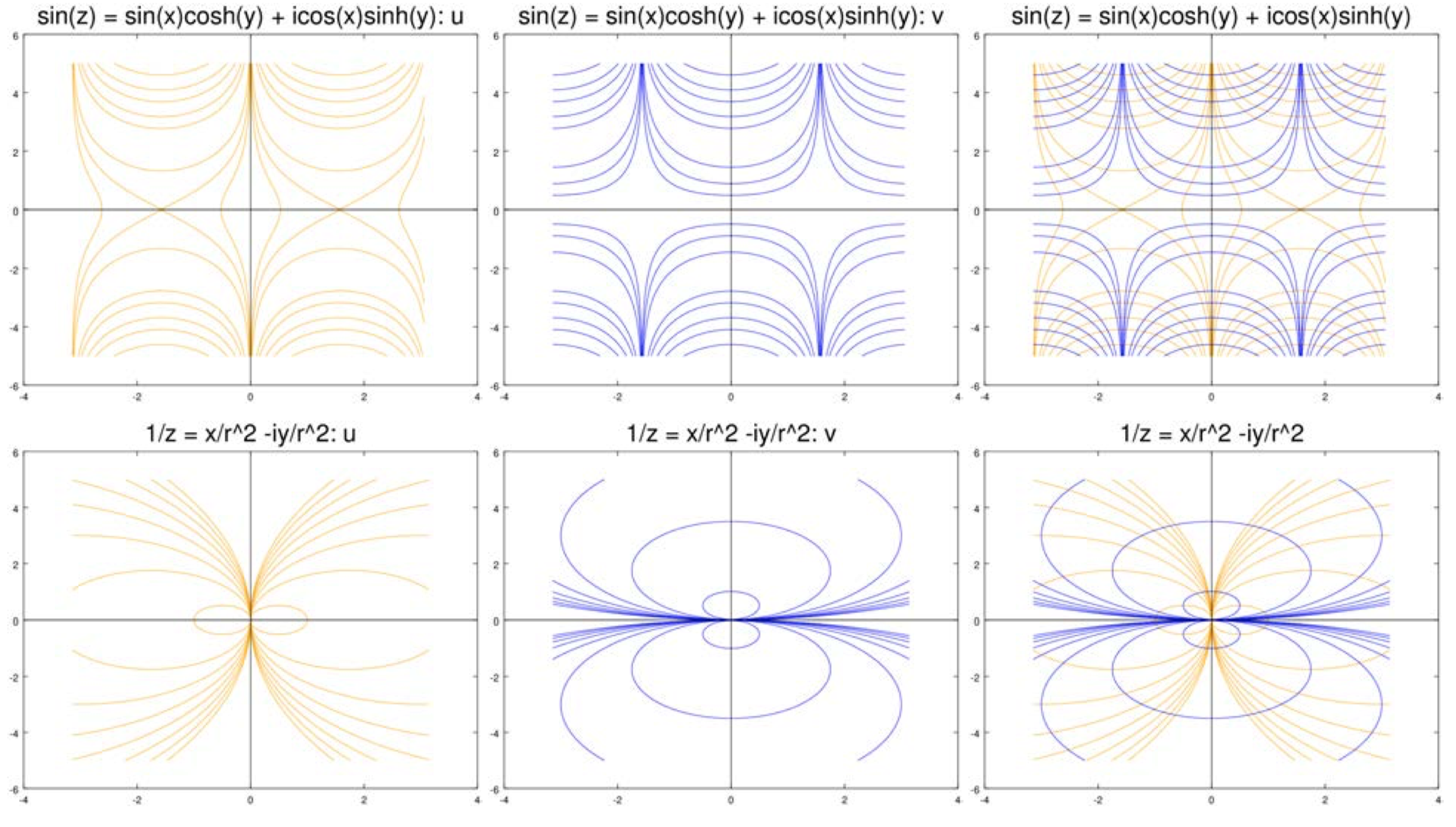
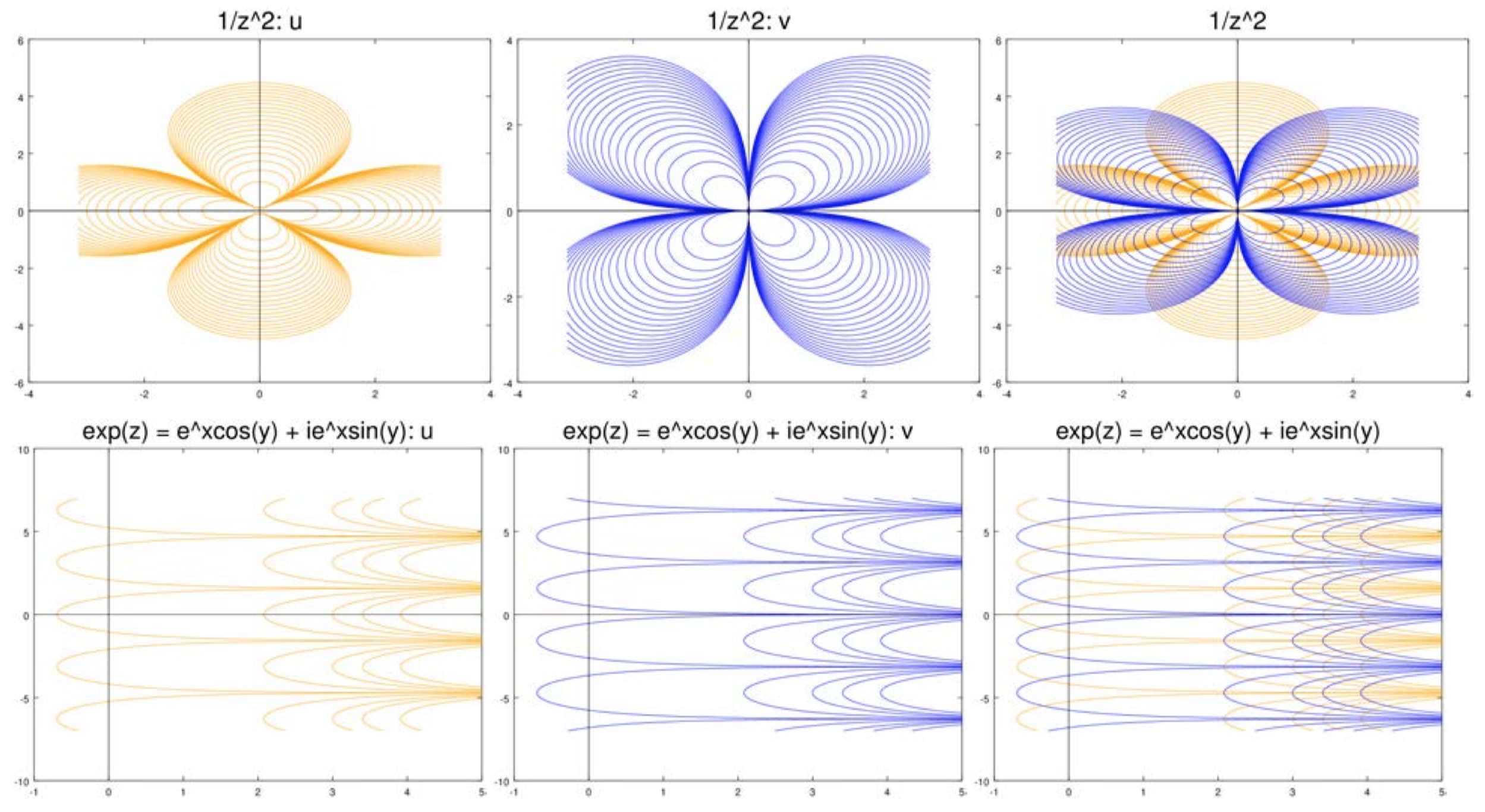
(i) Dejar
\[f(z) = z^2 = (x^2 - y^2) + i2xy,\]
Entonces
\[\nabla u = (2x, -2y) \text{ and } \nabla v = (2y, 2x).\]
Es trivial comprobarlo\(\nabla u \cdot \nabla v = 0\), por lo que son ortogonales.
ii) Dejar
\[f(z) = \dfrac{1}{z} = \dfrac{x}{r^2} - i \dfrac{y}{r^2}.\]
Por lo tanto, es fácil de calcular
\[\nabla u = (\dfrac{y^2 - x^2}{r^4}, \dfrac{-2xy}{r^4}) \text{ and } \nabla v = (\dfrac{2xy}{r^4}, \dfrac{y^2 - x^2}{r^4}).\]
Nuevamente es trivial comprobar eso\(\nabla u \cdot \nabla v = 0\), por lo que son ortogonales.
Considerar
\[f(z) = z^2\]
Del ejemplo anterior tenemos
\[u(x, y) = x^2 - y^2, \ \ \ v(x, y) = 2xy, \ \ \ \nabla u = (2x, -2y), \ \ \ \nabla v = (2y, 2x).\]
At\(z = 0\), los gradientes son ambos 0 por lo que el teorema sobre ortogonalidad no se aplica.
Veamos las curvas de nivel a través del origen. La curva de nivel (realmente el 'conjunto de niveles') para
\[u = x^2 - y^2 = 0\]
es el par de líneas\(y = \pm x\). En el origen esta no es una curva suave.
Mira las cifras de\(z^2\) arriba. Sí parece que lejos del origen las curvas de nivel de\(u\) intersectan las líneas donde\(v = 0\) en ángulo recto. Lo mismo es cierto para las curvas de nivel de\(v\) y las líneas donde\(u = 0\). Se puede ver la degeneración que se forma en el origen: a medida que las curvas de nivel se dirigen hacia 0 se ponen más puntiagudos y en ángulo más recto. Por lo que la curva de nivel\(u = 0\) es más propiamente pensada como cuatro ángulos rectos. La curva de nivel de\(u = 0\), sin saber qué tramo de\(v = 0\) intersectar ortogonalmente toma el promedio y entra en el origen a 45\(^{\circ}\).