6.1: Puntos Ordinarios
- Page ID
- 116872
Si\(x_0\) es un punto ordinario de (6.1), entonces es posible determinar dos soluciones de series de potencia (es decir, serie Taylor) para\(y = y(x)\) centrado en\(x = x_0\). Ilustramos el método de solución resolviendo dos ejemplos, con\(x_0 = 0\).
Encuentra la solución general de\(y''+y=0\).
Solución
A estas alturas, ya debes saber que la solución general es\(y(x) = a_0 \cos x + a_1 \sin x\), con\(a_0\) y\(a_1\) constantes. Para encontrar una solución de series de potencia sobre el punto\(x_0 = 0\), escribimos\[y(x)=\sum\limits_{n=0}^{\infty}a_nx^n;\nonumber\] y al diferenciar término por término\[y'(x)=\sum\limits_{n=1}^{\infty}na_nx^{n-1},\nonumber\] y\[y''(x)=\sum\limits_{n=2}^{\infty}n(n-1)a_nx^{n-2}.\nonumber\]
Sustituyendo la serie de\(y\) potencias y sus derivadas en la ecuación diferencial a resolver, obtenemos \[\label{eq:1}\sum\limits_{n=2}^{\infty}n(n-1)a_nx^{n-2}+\sum\limits_{n=0}^{\infty}a_nx^n=0.\]
El método de solución de la serie de potencia requiere combinar las dos sumas en el lado izquierdo de\(\eqref{eq:1}\) en una sola serie de potencia en\(x\). Para desplazar el exponente de\(x^{n−2}\) en la primera suma hacia arriba en dos para obtener\(x^n\), necesitamos desplazar el índice de suma hacia abajo en dos; es decir,\[\sum\limits_{n=2}^{\infty}n(n-1)a_nx^{n-2}=\sum\limits_{n=0}^{\infty}(n+2)(n+1)a_{n+2}x^n.\nonumber\]
Luego podemos combinar las dos sumas\(\eqref{eq:1}\) para obtener \[\label{eq:2}\sum\limits_{n=0}^{\infty}\left((n+2)(n+1)a_{n+2}+a_n\right)x^n=0.\]
\(\eqref{eq:2}\)Para que se satisfagan, el coeficiente de cada potencia de\(x\) debe desaparecer por separado. (Esto se puede probar fijando\(x = 0\) después de la diferenciación sucesiva). Por lo tanto, obtenemos la relación de recurrencia\[a_{n+2}=-\frac{a_n}{(n+2)(n+1)},\quad n=0,1,2,\ldots\nonumber\]
Observamos que los coeficientes pares e impares se desacoplan. Se obtienen así dos secuencias independientes comenzando con el primer término\(a_0\) o\(a_1\). Desarrollando estas secuencias, tenemos para la secuencia que comienza con\(a_0\):
\[\begin{aligned}a_0&, \\ a_2&=-\frac{1}{2}a_0, \\ a_4&=-\frac{1}{4\cdot 3}a_2=\frac{1}{4\cdot 3\cdot 2}a_0, \\ a_6&=-\frac{1}{6\cdot 5}a_4=-\frac{1}{6!}a_0;\end{aligned}\]y el coeficiente general en esta secuencia para\(n = 0, 1, 2,\ldots\) es\[a_{2n}=\frac{(-1)^n}{(2n)!}a_0.\nonumber\]
Además, para la secuencia que comienza con\(a_1\):
\[\begin{aligned}a_1&, \\ a_3&=-\frac{1}{3\cdot 2}a_1, \\ a_5&=-\frac{1}{5\cdot 4}a_3=\frac{1}{5\cdot 4\cdot 3\cdot 2}a_1, \\ a_7&=-\frac{1}{7\cdot 6}a_5=-\frac{1}{7!}a_1;\end{aligned}\]y el coeficiente general en esta secuencia para\(n = 0, 1, 2,\ldots\) es\[a_{2n+1}=\frac{(-1)^n}{(2n+1)!}a_1.\nonumber\]
Utilizando el principio de superposición, la solución general es,\[\begin{aligned}y(x)&=a_0\sum\limits_{n=0}^\infty\frac{(-1)^n}{(2n)!}x^{2n}+a_1\sum\limits_{n=0}^\infty\frac{(-1)^n}{(2n+1)!}x^{2n+1} \\ &=a_0\left(1-\frac{x^2}{2!}+\frac{x^4}{4!}-\cdots\right)+a_1\left(x-\frac{x^3}{3!}+\frac{x^5}{5!}-\cdots\right) \\ &=a_0\cos x+a_1\sin x,\end{aligned}\] pues, la esperada.
En nuestro siguiente ejemplo, resolveremos la Ecuación de Airy. Esta ecuación diferencial surge en el estudio de la óptica, la mecánica de fluidos y la mecánica cuántica.
Encuentra la solución general de\(y''-xy=0\).
Solución
Con\[y(x)=\sum\limits_{n=0}^\infty a_nx^n,\nonumber\] la ecuación diferencial se convierte \[\label{eq:3}\sum\limits_{n=2}^\infty n(n-1)a_nx^{n-2}-\sum\limits_{n=0}^\infty a_nx^{n+1}=0.\]
Desplazamos la primera suma a\(x^{n+1}\) desplazando el exponente hacia arriba en tres, es decir,\[\sum\limits_{n=2}^\infty n(n-1)a_nx^{n-2}=\sum\limits_{n=-1}^\infty (n+3)(n+2)a_{n+3}x^{n+1}.\nonumber\]
Al combinar las dos sumas en\(\eqref{eq:3}\), separamos el\(n = −1\) término extra en la primera suma dada por\(2a_2\). Por lo tanto,\(\eqref{eq:3}\) se convierte \[\label{eq:4}2a_2+\sum\limits_{n=0}^\infty\left((n+3)(n+2)a_{n+3}-a_n\right)x^{n+1}=0.\]
Estableciendo coeficientes de potencias de\(x\) a cero, primero encontramos\(a_2 = 0\), y luego obtenemos la relación de recursión \[\label{eq:5}a_{n+3}=\frac{1}{(n+3)(n+2)}a_n.\]
Tres secuencias de coeficientes—aquellos que comienzan con uno\(a_0,\: a_1\) o\(a_2\) —desacople. En particular, las tres secuencias son\[\begin{array}{l}a_0,a_3,a_6,a_9,\ldots ; \\ a_1,a_4,a_7,a_{10},\ldots ; \\ a_2,a_5,a_8,a_{11}\ldots\end{array}\nonumber\]
Ya que\(a_2 = 0\), encontramos inmediatamente para la última secuencia\[a_2=a_5=a_8=a_{11}=\cdots =0.\nonumber\]
Calculamos los primeros cuatro términos distintos de cero en la serie de potencias con coeficientes correspondientes a las dos primeras secuencias. Empezando con\(a_0\), tenemos\[\begin{aligned}a_0&, \\ a_3&=\frac{1}{3\cdot 2}a_0, \\ a_6&=\frac{1}{6\cdot 5\cdot 3\cdot 2}a_0, \\ a_9&=\frac{1}{9\cdot 8\cdot 6\cdot 5\cdot 3\cdot 2}a_0;\end{aligned}\] y comenzando con\(a_1\),\[\begin{aligned}a_1&, \\ a_4&=\frac{1}{4\cdot 3}a_1, \\ a_7&=\frac{1}{7\cdot 6\cdot 4\cdot 3}a_1, \\ a_{10}&=\frac{1}{10\cdot 9\cdot 7\cdot 6\cdot 4\cdot 3}a_1.\end{aligned}\]
La solución general para\(y = y(x)\), por lo tanto, puede escribirse como\[\begin{aligned}y(x)&=a_0\left(1+\frac{x^3}{6}+\frac{x^6}{180}+\frac{x^9}{12960}+\cdot\right) +a_1\left(x+\frac{x^4}{12}+\frac{x^7}{504}+\frac{x^{10}}{45360}+\cdot\right) \\ &=a_0y_0(x)+a_1y_1(x).\end{aligned}\]
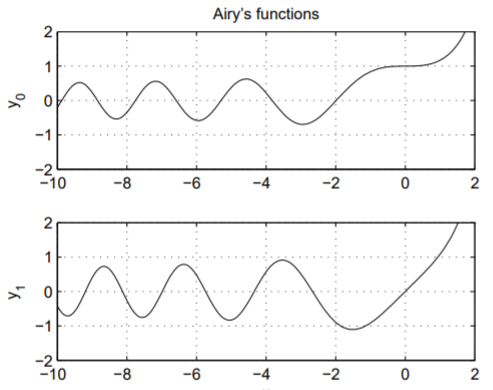
Supongamos que nos gustaría graficar las soluciones\(y = y_0(x)\) y\(y = y_1(x)\) versus\(x\) resolviendo la ecuación diferencial\(y'' − xy = 0\) numéricamente. ¿Qué condiciones iniciales debemos usar? Claramente,\(y = y_0(x)\) resuelve la oda con valores iniciales\(y(0) = 1\) y\(y' (0) = 0\), mientras\(y = y_1(x)\) resuelve la oda con valores iniciales\(y(0) = 0\) y\(y' (0) = 1\).
Las soluciones numéricas, obtenidas con MATLAB, se muestran en la Fig. \(\PageIndex{1}\). Tenga en cuenta que las soluciones oscilan para negativo\(x\) y crecen exponencialmente para positivo\(x\). Esto se puede entender recordando que\(y''+ y = 0\) tiene soluciones oscilatorias de seno y coseno y\(y'' − y = 0\) tiene soluciones de seno y coseno hiperbólico exponencial.
