5.5: Integración Numérica
- Page ID
- 111793
El Teorema Fundamental del Cálculo da una técnica concreta para encontrar el valor exacto de una integral definida. Esa técnica se basa en la computación antiderivados. A pesar del poder de este teorema, todavía hay situaciones en las que debemos aproximar el valor de la integral definida en lugar de encontrar su valor exacto. La primera situación que exploramos es donde no podemos calcular la antiderivada del integrando. El segundo caso es cuando en realidad no conocemos el integrando, sino solo su valor cuando se evalúa en ciertos puntos.
Una función elemental es cualquier función que sea una combinación de polinomios,\(n^{\text{th}}\) raíces, funciones racionales, exponenciales, logarítmicas y trigonométricas. Podemos calcular la derivada de cualquier función elemental, pero hay muchas funciones elementales de las cuales no podemos calcular una antiderivada. Por ejemplo, las siguientes funciones no tienen antiderivadas que podamos expresar con funciones elementales:
$$e^ {-x^2},\ quad\ sin (x^3)\ quad\ texto {y}\ quad\ frac {\ sin x} {x}.\]
La forma más sencilla de referirse a las antiderivadas de\(e^{-x^2}\) es simplemente escribir\(\int e^{-x^2}\ dx\).
En esta sección se describen tres métodos comunes para aproximar el valor de integrales definidas. Describimos cada uno como un método sistemático de aproximación del área bajo una curva. Al aproximar esta área con precisión, encontramos una aproximación precisa de la integral definida correspondiente.
Aplicaremos los métodos que aprendamos en esta sección a las siguientes integrales definidas:
$$\ int_0^1 e^ {-x^2}\ dx,\ quad\ int_ {-\ frac {\ pi} {4}} ^ {\ frac {\ pi} {2}}\ sin (x^3)\ dx,\ quad\ texto {y}\ quad\ int_ {0.5} ^ {4\ pi}\ frac {\ sin (x)} {x} dx,\]
como se muestra en la Figura\(\PageIndex{1}\).
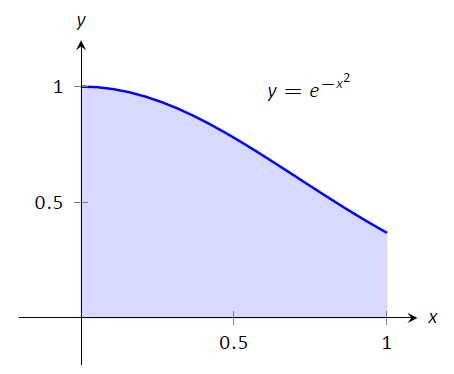
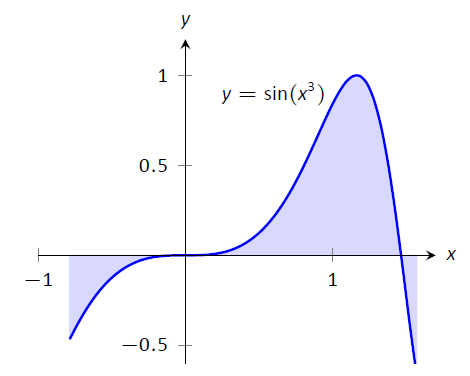
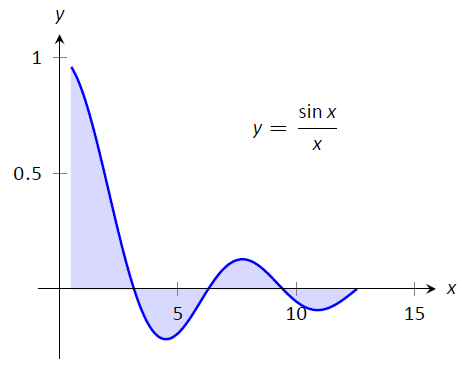
Figura\(\PageIndex{1}\): Representando gráficamente tres integrales definidas que no pueden ser evaluadas usando antiderivados.
Los métodos de la regla de la mano izquierda y derecha
En la Sección 5.3 abordamos el problema de evaluar integrales definidas aproximando el área bajo la curva usando rectángulos. Repasamos esas ideas aquí antes de introducir otros métodos de aproximación de integrales definidas.
Comenzamos con una revisión de la notación. Dejar\(f\) ser una función continua en el intervalo\([a,b]\). Deseamos aproximar\(\int_a^b f(x)\ dx\). Particionamos\([a,b]\) en subintervalos\(n\) igualmente espaciados, cada uno de longitud\(dx = \frac{b-a}{n}\). Los puntos finales de estos subintervalos se etiquetan como
$$x_1=a,\ x_2 = a+dx,\ x_3 = a+ 2dx,\\ lpuntos,\ x_i = a+ (i-1)\ dx,\\ ldots,\ x_ {n+1} = b.\]
La Idea Clave 8 establece que para usar la Regla de Mano Izquierda usamos la suma\( \sum_{i=1}^n f(x_i)\ dx\) y para usar la Regla de Mano Derecha que usamos\( \sum_{i=1}^n f(x_{i+1})\ dx\). Revisamos el uso de estas reglas en el contexto de ejemplos.
Ejemplo\(\PageIndex{1}\): Approximating definite integrals with rectangles
Aproximado\( \int_0^1e^{-x^2}\ dx\) usando las Reglas de Mano Izquierda y Derecha con 5 subintervalos igualmente espaciados.
Solución
Comenzamos dividiendo el intervalo\([0,1]\) en 5 intervalos igualmente espaciados. Tenemos\(dx = \frac{1-0}5 = 1/5=0.2\), entonces $$x_1 = 0,\ x_2 = 0.2,\ x_3 = 0.4,\ x_4 = 0.6,\ x_5 = 0.8,\\ text {y}\ x_6 = 1.\]
Usando la Regla de la Mano Izquierda, tenemos:
\[\begin{align} \sum_{i=1}^n f(x_i)\ dx &= \big(f(x_1)+f(x_2) + f(x_3) + f(x_4) + f(x_5)\big)\ dx \\ &= \big(f(0) + f(0.2) + f(0.4) + f(0.6) + f(0.8)\big)\ dx \\ &\approx \big(1+0.961 + 0.852 + 0.698 + 0.527)(0.2)\\ &\approx 0.808.\end{align}\]
Usando la Regla de la Mano Derecha, tenemos:
\ [\ begin {align}\ sum_ {i=1} ^n f (x_ {i+1})\ dx &=\ grande (f (x_2) + f (x_3) + f (x_4) + f (x_5) +f (x_6)\ grande)\ dx\ &=\ grande (f (0.2) + f (0.4) + f (0.6) + f (0.6) + f (0.8) +f (1)\ grande)\ dx\\ &\ approx\ grande (0.961 +0.852 + 0.698 + 0.527 + 0.368) (0.2)\\ &\ aprox 0.681.
\ end {align}\]
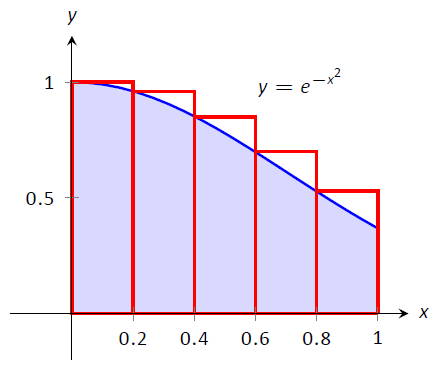
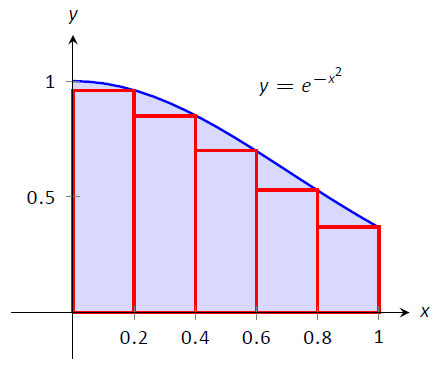
Figura\(\PageIndex{2}\): Aproximación\(\int_0^1e^{-x^2}\ dx\) en el Ejemplo\(\PageIndex{1}\)
La figura\(\PageIndex{2}\) muestra los rectángulos utilizados en cada método para aproximar la integral definida. Estas gráficas muestran que en este caso particular, la Regla de la Mano Izquierda es una sobreaproximación y la Regla de la Mano Derecha es una subaproximación. Para obtener una mejor aproximación, podríamos usar más rectángulos, como hicimos en la Sección 3.1. También podríamos promediar los resultados de la Regla de Mano Izquierda y Derecha juntos, dando
$$\ frac {0.808 + 0.681} {2} = 0.7445.\]
La respuesta real, exacta a 4 lugares después del decimal, es 0.7468, mostrando que nuestro promedio es una buena aproximación.
Ejemplo\(\PageIndex{2}\): Approximating definite integrals with rectangles
Aproximado\(\int_{-\frac{\pi}4}^{\frac{\pi}2} \sin (x^3)\ dx\) usando las Reglas de Mano Izquierda y Derecha con 10 subintervalos igualmente espaciados.
Solución
Comenzamos por encontrar\ Delta x:
$$\ frac {b-a} {n} =\ frac {\ pi/2 - (-\ pi/4)} {10} =\ frac {3\ pi} {40}\ aprox 0.236.\]
Es útil escribir los puntos finales de los subintervalos en una tabla; en Tabla\(\PageIndex{1}\), damos los valores exactos de los puntos finales, sus aproximaciones decimales y aproximaciones decimales de\(\sin(x^3)\) evaluados en estos puntos.
| \(x_i\) | Exacto | Aprox. | \(\sin(x_i^3)\) |
|---|---|---|---|
| \ (x_i\) ">\(x_1\) | \(-\pi/4\) | \(-0.785\) | \ (\ sin (x_i^3)\) ">\(-0.466\) |
| \ (x_i\) ">\(x_2\) | \(-7 \pi/40\) | \(-0.550\) | \ (\ sin (x_i^3)\) ">\(-0.165\) |
| \ (x_i\) ">\(x_3\) | \(-{\pi }/{10}\) | \(-0.314\) | \ (\ sin (x_i^3)\) ">\(-0.031\) |
| \ (x_i\) ">\(x_4\) | \(-{\pi }/{40}\) | \(-0.0785\) | \ (\ sin (x_i^3)\) ">\(0\) |
| \ (x_i\) ">\(x_5\) | \({\pi }/{20}\) | 0.157 | \ (\ sin (x_i^3)\) ">0.004 |
| \ (x_i\) ">\(x_6\) | \({\pi }/{8}\) | 0.393 | \ (\ sin (x_i^3)\) ">0.061 |
| \ (x_i\) ">\(x_7\) | \({\pi }/{5}\) | 0.628 | \ (\ sin (x_i^3)\) ">0.246 |
| \ (x_i\) ">\(x_8\) | \({11 \pi }/{40}\) | 0.864 | \ (\ sin (x_i^3)\) ">0.601 |
| \ (x_i\) ">\(x_9\) | \({7 \pi }/{20}\) | 1.10 | \ (\ sin (x_i^3)\) ">0.971 |
| \ (x_i\) ">\(x_{10}\) | \({17 \pi }/{40}\) | 1.34 | \ (\ sin (x_i^3)\) ">0.690 |
| \ (x_i\) ">\(x_{11}\) | \({\pi}/{2}\) | 1.57 | \ (\ sin (x_i^3)\) ">\(-0.670\) |
Una vez creada esta tabla, es sencillo aproximar la integral definida usando las Reglas de Mano Izquierda y Derecha. (Nota: la tabla en sí es fácil de crear, especialmente con un programa de hoja de cálculo estándar en una computadora. Las dos últimas columnas son todo lo que se necesita.) La Regla de la Mano Izquierda suma los 10 primeros valores de\(\sin(x_i^3)\) y multiplica la suma por\(dx\); la Regla de la Mano Derecha suma los últimos 10 valores de\(\sin(x_i^3)\) y se multiplica por\(dx\). Por lo tanto tenemos:
Regla de la mano izquierda:\(\int_{-\frac{\pi}4}^{\frac{\pi}2}\sin(x^3)\ dx \approx (1.91)(0.236) = 0.451.\)
Regla de la mano derecha:\(\int_{-\frac{\pi}4}^{\frac{\pi}2}\sin(x^3)\ dx \approx (1.71)(0.236) = 0.404.\)
Promedio de las Reglas de Mano Izquierda y Derecha: 0.4275.
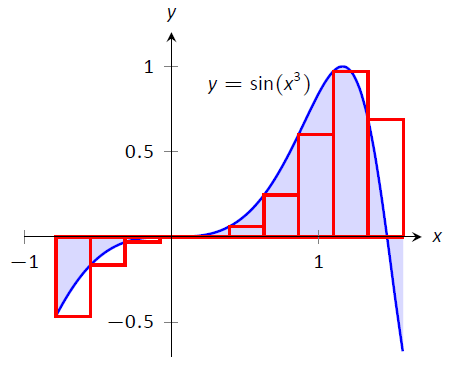
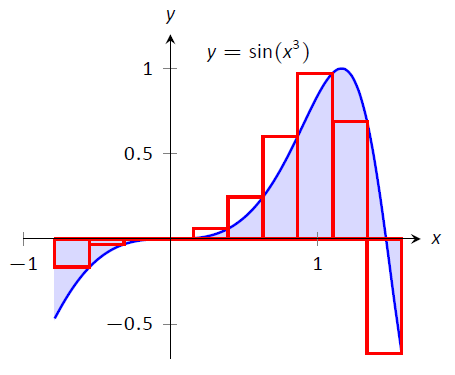
Figura\(\PageIndex{3}\):\(\int_{-\frac{\pi}4}^{\frac{\pi}2}\sin(x^3)\ dx\) en Ejemplo\(\PageIndex{2}\)
La respuesta real, exacta a 3 lugares después del decimal, es 0.460. Nuestras aproximaciones volvieron a ser bastante buenas. Los rectángulos utilizados en cada aproximación se muestran en la Figura\(\PageIndex{3}\). De las gráficas queda claro que el uso de más rectángulos (y por lo tanto, rectángulos más estrechos) debería dar como resultado una aproximación más precisa.
La regla trapezoidal
En Ejemplo\(\PageIndex{1}\) aproximamos el valor de\(\int_0^1 e^{-x^2}\ dx\) con 5 rectángulos de igual ancho. La figura\(\PageIndex{2}\) muestra los rectángulos utilizados en las Reglas de Mano Izquierda y Derecha. Estas gráficas muestran claramente que los rectángulos no coinciden tan bien con la forma de la gráfica, y que las aproximaciones precisas solo vendrán usando muchos rectángulos.
En lugar de usar rectángulos para aproximar el área, podemos usar trapecios. En la Figura\(\PageIndex{4}\), se muestra la región inferior\(f(x) = e^{-x^2}\)\([0,1]\) aproximadamente con 5 trapecios de igual ancho; las “esquinas” superiores de cada trapecio se encuentran en la gráfica de\(f(x)\). Es claro a partir de esta cifra que estos trapezoides se aproximan con mayor precisión al área inferior\(f\) y por lo tanto deberían dar una mejor aproximación de\(\int_0^1 e^{-x^2}\ dx\). (De hecho, estos trapecios parecen dar una gran aproximación de la zona!)
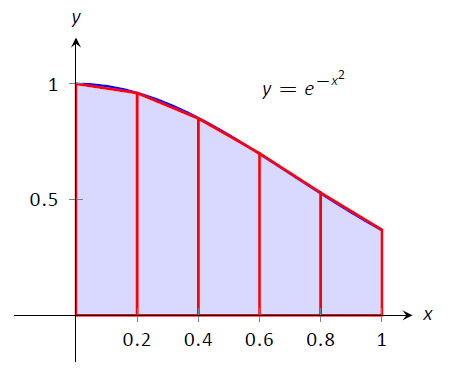
Figura\(\PageIndex{4}\): Aproximación\(\int_0^1 e^{-x^2}\ dx\) usando 5 trapecios de anchos iguales.
La fórmula para el área de un trapecio se da en la Figura\(\PageIndex{5}\). Aproximamos\(\int_0^1 e^{-x^2}\ dx\) con estos trapecios en el siguiente ejemplo.
Ejemplo\(\PageIndex{3}\): Approximating definite integrals using trapezoids
Use 5 trapecios de igual ancho para aproximarse\(\int_0^1e^{-x^2}\ dx\).
Solución
Para calcular las áreas de los 5 trapecios en la Figura\(\PageIndex{6}\), nuevamente será útil crear una tabla de valores como se muestra en Tabla\(\PageIndex{2}\).
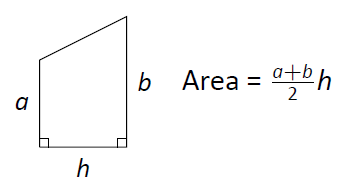
Figura\(\PageIndex{5}\): El área de un trapecio
| \(x_i\) | \(e^{-x_i^2}\) |
|---|---|
| \ (x_i\) ">0 | \ (e^ {-x_i^2}\) ">1 |
| \ (x_i\) ">0.2 | \ (e^ {-x_i^2}\) ">0.961 |
| \ (x_i\) ">0.4 | \ (e^ {-x_i^2}\) ">0.852 |
| \ (x_i\) ">0.6 | \ (e^ {-x_i^2}\) ">0.698 |
| \ (x_i\) ">0.8 | \ (e^ {-x_i^2}\) ">0.527 |
| \ (x_i\) ">1 | \ (e^ {-x_i^2}\) ">0.368 |
El trapecio más a la izquierda tiene patas de longitud 1 y 0.961 y una altura de 0.2. Así, por nuestra fórmula, el área del trapecio más a la izquierda es:
$$\ frac {1+0.961} {2} (0.2) = 0.1961.\]
Moviéndose a la derecha, el siguiente trapecio tiene patas de longitud 0.961 y 0.852 y una altura de 0.2. Así su área es:
$\ frac {0.961+0.852} 2 (0.2) = 0.1813.\]
La suma de las áreas de los 5 trapecios es:
\[\begin{align} \frac{1+0.961}{2}(0.2) + \frac{0.961+0.852}2(0.2)+\frac{0.852+0.698}2(0.2)&+ \\ \frac{0.698+0.527}2(0.2)+\frac{0.527+0.368}2(0.2)&= 0.7445. \end{align}\]
Nos aproximamos\(\int_0^1 e^{-x^2}\ dx \approx 0.7445.\)
Hay muchas cosas que observar en este ejemplo. Obsérvese cómo cada término en la suma final se multiplicó tanto por 1/2 como por\(dx = 0.2\). Podemos facturar estos coeficientes, dejando una suma más concisa como:
$$\ frac12 (0.2)\ Grande [(1+0.961) + (0.961+0.852) + (0.852+0.698) + (0.698+ 0.527) + (0.527 + 0.368)\ Grande].\]
Ahora note que todos los números excepto el primero y el último se suman dos veces. Por lo tanto podemos escribir la suma aún más concisa como
$$\ frac {0.2} {2}\ Grande [1 + 2 (0.961+0.852+0.698+0.527) + 0.368\ Grande].\]
Este es el corazón de la Regla Trapezoidal, en donde\(\int_a^b f(x) \ dx\) se aproxima una integral definida mediante el uso de trapecios de iguales anchuras para aproximarse al área correspondiente debajo\(f\). Usando subintervalos\(n\) igualmente espaciados con puntos finales\(x_1\)\(x_2\),\(\ldots\),\(x_{n+1}\),, nuevamente tenemos\( \Delta x = \frac{b-a}n\). Por lo tanto:
\[\begin{align} \int_a^b f(x)\ dx & \approx \sum_{i=1}^n \frac{f(x_i)+f(x_{i+1})}2\ dx \\ & = \frac{\ dx}2 \sum_{i=1}^n \big(f(x_i)+f(x_{i+1})\big)\\ & = \frac{\ dx}2\Big[f(x_1)+ 2\sum_{i=2}^n f(x_i) + f(x_{n+1})\Big].\end{align}\]
Ejemplo\(\PageIndex{4}\): Using the Trapezoidal Rule
Revisar Ejemplo\(\PageIndex{4}\) y aproximar\(\int_{-\frac{\pi}{4}}^{\frac{\pi}{2}} \sin (x^3)\ dx\) usando la Regla Trapezoidal y 10 subintervalos igualmente espaciados.
Solución
Nos referimos de nuevo a Tabla\(\PageIndex{1}\) para la tabla de valores de\(\sin(x^3)\). Recordemos eso\(dx = 3\pi/40 \approx 0.236\). Así tenemos:
\[\begin{align*}\int_{-\frac {\pi}4}^{\frac{\pi}2} \sin (x^3)\ dx &\approx \frac{0.236}{2}\Big[-0.466 + 2\Big(-0.165+(-0.031)+\ldots+0.69\Big)+(-0.67)\Big]\\ &= 0.4275. \end{align*}\]
Observe cuán “rápido” se puede implementar la Regla Trapezoidal una vez creada la tabla de valores. Esto es cierto para todos los métodos explorados en esta sección; el trabajo real es crear una tabla de\(x_i\) y\(f(x_i)\) valores. Una vez completado esto, aproximar la integral definida no es difícil. Nuevamente, usar la tecnología es sabio. Las hojas de cálculo pueden hacer un trabajo rápido de estos cálculos y facilitar el uso de muchos subintervalos.
Observe también las aproximaciones que da la Regla Trapezoidal. ¡Es el promedio de las aproximaciones dadas por las Reglas de la Mano Izquierda y Derecha! Esto efectivamente vuelve obsoletas las Reglas de la Mano Izquierda y Derecha. Son útiles cuando se aprende por primera vez sobre integrales definidas, pero si se necesita una aproximación real, generalmente es mejor usar la Regla Trapezoidal en lugar de la Regla Izquierda o Derecha.
¿Cómo podemos mejorar la Regla Trapezoidal, aparte de usar cada vez más trapecios? La respuesta es clara una vez que miramos hacia atrás y consideramos lo que realmente hemos hecho hasta ahora. La Regla de la Mano Izquierda no se trata realmente de usar rectángulos para aproximar el área. En cambio, se aproxima a una función\(f\) con funciones constantes en pequeños subintervalos y luego calcula la integral definida de estas funciones constantes. La Regla Trapezoidal es realmente aproximar una función\(f\) con una función lineal en un pequeño subintervalo, luego calcula la integral definida de esta función lineal. En ambos casos las integrales definidas son fáciles de calcular en términos geométricos.
Entonces tenemos una progresión: comenzamos por aproximarnos\(f\) con una función constante y luego con una función lineal. ¿Qué es lo siguiente? Una función cuadrática. Al aproximar la curva de una función con muchas parábolas, generalmente obtenemos una aproximación aún mejor de la integral definida. A este proceso lo llamamos Regla de Simpson, que lleva el nombre de Thomas Simpson (1710-1761), a pesar de que otros habían utilizado esta regla tanto como 100 años antes.
Regla de Simpson
Dado un punto, podemos crear una función constante que pase por ese punto. Dados dos puntos, podemos crear una función lineal que recorra esos puntos. Dados tres puntos, podemos crear una función cuadrática que pase por esos tres puntos (dado que no hay dos que tengan el mismo\(x\) valor —valor).
Considere tres puntos\((x_1,y_1)\),\((x_2,y_2)\) y\((x_3,y_3)\) cuyos\(x\) valores —están igualmente espaciados y\(x_1<x_2<x_3\). \(f\)Sea la función cuadrática que pasa por estos tres puntos. No es difícil demostrar que
\[\int_{x_1}^{x_3} f(x)\ dx = \frac{x_3-x_1}{6}\big(y_1+4y_2+y_3\big).\]
Considera Figura\(\PageIndex{6}\). Una función\(f\) pasa por los 3 puntos mostrados y la parábola\(g\) que también pasa por esos puntos se grafica con una línea discontinua. Usando nuestra ecuación de arriba, sabemos exactamente que $$\ int_1^3 g (x)\ dx =\ frac {3-1} {6}\ big (3+4 (1) +2\ big) = 3.$$ Ya que\(g\) es una buena aproximación para\(f\) on\([1,3]\), podemos afirmar que $$\ int_1^3 f (x)\ dx\ approx 3.\]
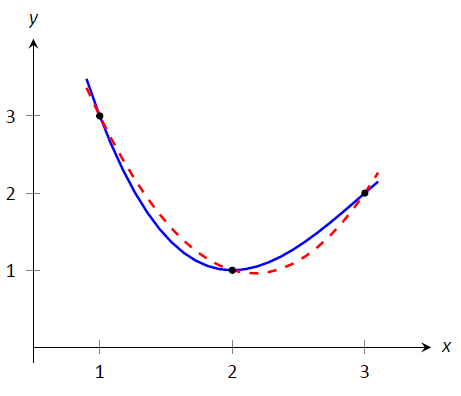
Figura\(\PageIndex{6}\): Gráfica de una función\(f\) y una parábola que la aproxima bien\([1,3]\).
Observe cómo el intervalo\([1,3]\) se dividió en dos subintervalos ya que necesitábamos 3 puntos. Debido a esto, cada vez que usamos la Regla de Simpson, necesitamos romper el intervalo en un número par de subintervalos.
En general, para aproximarse\(\int_a^b f(x)\ dx\) usando la Regla de Simpson,\([a,b]\) subdivide en\(n\) subintervalos, donde\(n\) es par y cada subintervalo tiene ancho\(\ dx = (b-a)/n\). Nos aproximamos\(f\) con curvas\(n/2\) parabólicas, usando Ecuación\(\PageIndex{22}\) para calcular el área bajo estas parábolas. Sumando estas áreas da la fórmula:
$$\ int_a^b f (x)\ dx\ approx\ frac {\ dx} 3\ Grande [f (x_1) +4f (x_2) +2f (x_3) +4f (x_4) +\ ldots+2f (x_ {n-1}) +4f (x_n) +f (x_ {n+1})\ Grande].]
Observe cómo los coeficientes de los términos en la suma tienen el patrón 1, 4, 2, 4, 2, 4,, 2, 4\(\ldots\), 2, 4, 1.
Demostremos la Regla de Simpson con un ejemplo concreto.
Ejemplo\(\PageIndex{5}\): Using Simpson's Rule
Aproximado\(\int_0^1 e^{-x^2}\ dx\) usando la Regla de Simpson y 4 subintervalos igualmente espaciados.
Solución
Comenzamos haciendo una tabla de valores como lo hemos hecho en el pasado, como se muestra en Tabla\(\PageIndex{3}\).
| \(x_i\) | \(e^{-x_i^2}\) |
|---|---|
| \ (x_i\) ">0 | \ (e^ {-x_i^2}\) ">1 |
| \ (x_i\) ">0.25 | \ (e^ {-x_i^2}\) ">0.939 |
| \ (x_i\) ">0.5 | \ (e^ {-x_i^2}\) ">0.779 |
| \ (x_i\) ">0.75 | \ (e^ {-x_i^2}\) ">0.570 |
| \ (x_i\) ">1 | \ (e^ {-x_i^2}\) ">0.368 |
La Regla de Simpson establece que
$$\ int_0^1e^ {-x^2}\ dx\ approx\ frac {0.25} {3}\ Grande [1+4 (0.939) +2 (0.779) +4 (0.570) + 0.368\ Grande] = 0.7468\ overline {3}.\]
Recordemos en Ejemplo\(\PageIndex{1}\) afirmamos que la respuesta correcta, exacta a 4 lugares después del decimal, fue 0.7468. ¡Nuestra aproximación con la Regla de Simpson, con 4 subintervalos, es mejor que nuestra aproximación con la Regla Trapezoidal usando 5!
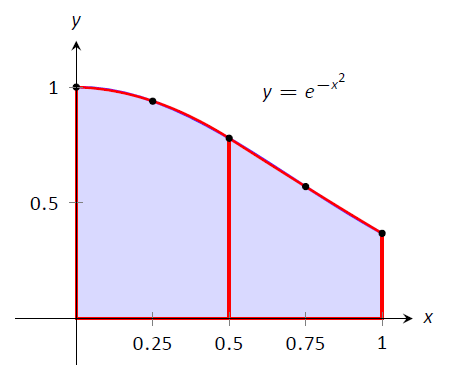
Figura\(\PageIndex{7}\): Usando la regla de Simpson con\(n=4\) para aproximar\(\int_0^1 e^{-x^2}\ dx\).
La figura\(\PageIndex{7}\) muestra\(f(x) = e^{-x^2}\) junto con sus parábolas aproximadas, demostrando lo buena que es nuestra aproximación. Las curvas de aproximación son casi indistinguibles de la función real.
Ejemplo\(\PageIndex{6}\): Using Simpson's Rule
Aproximado\(\int_{-\frac{\pi}4}^{\frac{\pi}2} \sin (x^3)\ dx\) usando la Regla de Simpson y 10 intervalos igualmente espaciados.
Solución
Tabla\(\PageIndex{4}\) muestra la tabla de valores que usamos en el pasado para este problema, se muestra aquí nuevamente por conveniencia. Nuevamente,\(\ dx = (\pi/2+\pi/4)/10 \approx 0.236\).
| \(x_i\) | \(\sin(x_i^3)\) |
|---|---|
| \ (x_i\) ">\(-0.785\) | \ (\ sin (x_i^3)\) ">\(-0.466\) |
| \ (x_i\) ">\(-0.550\) | \ (\ sin (x_i^3)\) ">\(-0.165\) |
| \ (x_i\) ">\(-0.314\) | \ (\ sin (x_i^3)\) ">\(-0.031\) |
| \ (x_i\) ">\(-0.0785\) | \ (\ sin (x_i^3)\) ">\(0\) |
| \ (x_i\) ">0.157 | \ (\ sin (x_i^3)\) ">0.004 |
| \ (x_i\) ">0.393 | \ (\ sin (x_i^3)\) ">0.061 |
| \ (x_i\) ">0.628 | \ (\ sin (x_i^3)\) ">0.246 |
| \ (x_i\) ">0.864 | \ (\ sin (x_i^3)\) ">0.601 |
| \ (x_i\) ">1.10 | \ (\ sin (x_i^3)\) ">0.971 |
| \ (x_i\) ">1.34 | \ (\ sin (x_i^3)\) ">0.690 |
| \ (x_i\) ">1.57 | \ (\ sin (x_i^3)\) ">\(-0.670\) |
La Regla de Simpson establece que
\[\begin{align}\int_{-\frac{\pi}4}^{\frac{\pi}2} \sin (x^3)\ dx &\approx \frac{0.236}3\Big[(-0.466)+4(-0.165)+2(-0.031) + \ldots \\ & \ldots + 2(0.971) + 4(0.69) + (-0.67)\big]\\ &= 0.4701\end{align}\]
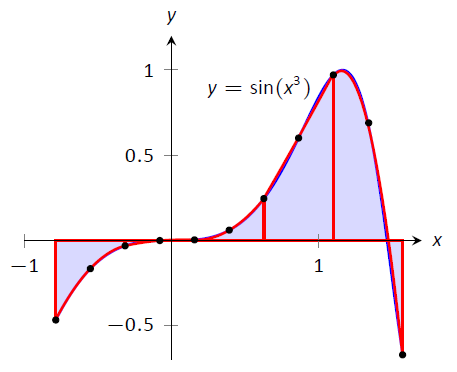
Figura\(\PageIndex{8}\): Aproximación\(\int_{-\frac{\pi}4}^{\frac{\pi}2}\sin(x^3)\ dx\) en Ejemplo\(\PageIndex{6}\) con la Regla de Simpson y 10 intervalos igualmente espaciados.
Recordemos que el valor real, exacto a 3 decimales, es 0.460. Nuestra aproximación está dentro de un 1/100\(^\text{th}\) del valor correcto. La gráfica de la Figura\(\PageIndex{8}\) muestra qué tan cerca coinciden las parábolas con la forma de la gráfica.
Resumen y Análisis de Errores
Resumimos los conceptos clave de esta sección hasta el momento en la siguiente Idea Clave.
Idea Clave 9: Integración Numérica
Dejar\(f\) ser una función continua on\([a,b]\), let\(n\) ser un entero positivo, y let\(\Delta x = \frac{b-a}{n}\).
Establecer\(x_1=a\),\(x_2 = a+\ dx\),\(\ldots\),\(x_i = a+(i-1)\ dx\),\(x_{n+1}=b\).
Considerar\(\int_a^b f(x)\ dx\).
Regla de la Mano Izquierda:\(\int_a^b f(x)\ dx \approx \ dx\Big[f(x_1) + f(x_2) + \ldots + f(x_n)\big]\).
Regla de la Mano Derecha:\(\int_a^b f(x)\ dx \approx \ dx\Big[f(x_2) + f(x_3) + \ldots + f(x_{n+1})\big]\).
Regla Trapezoidal:\(\int_a^b f(x)\ dx \approx \frac{\ dx}2\Big[f(x_1) + 2f(x_2) + 2f(x_3) +\ldots + 2f(x_n)+ f(x_{n+1})\big]\).
Regla de Simpson:\(\int_a^b f(x)\ dx \approx \frac{\ dx}3\Big[f(x_1) + 4f(x_2) + 2f(x_3) +\ldots + 4f(x_n)+ f(x_{n+1})\big]\) (\(n\)par)}.
En nuestros ejemplos, aproximamos el valor de una integral definida usando un método dado y luego la comparamos con la respuesta “correcta”. Esto debería haber planteado varias preguntas en la mente del lector, tales como:
- ¿Cómo se computó la respuesta “correcta”?
- Si se encuentra la respuesta correcta, ¿cuál es el punto de aproximarse?
- Si hay valor para aproximar, ¿cómo se supone que debemos saber si la aproximación es buena?
Estas son buenas preguntas, y sus respuestas son educativas. En los ejemplos, nunca se computó la respuesta correcta. Más bien, se dio una aproximación exacta a un cierto número de lugares después del decimal. En Ejemplo\(\PageIndex{1}\), no sabemos la respuesta exacta, pero sabemos que comienza con 0.7468. Estas aproximaciones más precisas se computaron mediante integración numérica pero con mayor precisión (es decir, más subintervalos y la ayuda de una computadora).
Como no se puede encontrar la respuesta exacta, la aproximación aún tiene su lugar. ¿Cómo vamos a saber si la aproximación es buena?
“Prueba y error” proporciona una manera. Usando la tecnología, haga una aproximación con, digamos, 10, 100 y 200 subintervalos. Esto probablemente no tomará mucho tiempo en absoluto, y debería surgir una tendencia. Si no surge una tendencia, intente usar aún más subintervalos. Ten en cuenta que el ensayo y error nunca es infalible; podrías tropezar con un problema en el que no surja una tendencia.
Un segundo método es utilizar el Análisis de Errores. Si bien los detalles están más allá del alcance de este texto, existen algunas fórmulas que dan límites a lo buena que será tu aproximación. Por ejemplo, la fórmula podría afirmar que la aproximación está dentro de 0.1 de la respuesta correcta. Si la aproximación es 1.58, entonces se sabe que la respuesta correcta está entre 1.48 y 1.68. Al usar muchos subintervalos, uno puede obtener una aproximación tan precisa como le gusta. El teorema\(\PageIndex{1}\) afirma cuáles son estos límites.
Teorema\(\PageIndex{1}\): Error Bounds in the Trapezoidal and Simpson's Rules
- \(E_T\)Sea el error al aproximar\( \int_a^b f(x)\ dx\) usando la Regla Trapezoidal.
Si\(f\) tiene una\(^\text{nd}\) derivada continua de 2\([a,b]\) y\(M\) es cualquier límite superior de\(\big|f"(x)\big|\) on\([a,b]\), entonces
$$ E_T\ leq\ frac {(b-a) ^3} {12n^2} M.\]
- \(E_S\)Sea el error al aproximar\( \int_a^b f(x)\ dx\) usando la Regla de Simpson.
Si\(f\) tiene una\(^\text{th}\) derivada continua de 4\([a,b]\) y\(M\) es cualquier límite superior de\(\big|f\,^{(4)}\big|\) on\([a,b]\), entonces
$$E_S\ leq\ frac {(b-a) ^5} {180n^4} M.\]
Hay algunas cosas clave a tener en cuenta sobre este teorema.
- Cuanto mayor sea el intervalo, mayor será el error. Esto debería tener sentido intuitivamente.
- El error se reduce a medida que se utilizan más subintervalos (es decir, a medida que\(n\) se hace más grande).
- El error en la Regla de Simpson tiene un término relativo a la 4\(^{\text{th}}\) derivada de\(f\). Considera un polinomio cúbico: su\(4^{\text{th}}\) derivado es 0. Por lo tanto, el error al aproximar la integral definida de un polinomio cúbico con la Regla de Simpson es 0 — ¡La Regla de Simpson calcula la respuesta exacta!
Revisamos Ejemplos\(\PageIndex{3}\)\(\PageIndex{5}\) y calculamos los límites de error usando Teorema\(\PageIndex{1}\) en el siguiente ejemplo.
Ejemplo\(\PageIndex{7}\): Computing error bounds
Encuentra los límites de error al aproximar\( \int_0^1 e^{-x^2}\ dx\) usando la Regla Trapezoidal y 5 subintervalos, y usando la Regla de Simpson con 4 subintervalos.
Solución
Regla Trapezoidal con\(n=5\):
Comenzamos por computar la\(2^\text{nd}\) derivada de\(f(x) = e^{-x^2}\):
\[f"(x) = e^{-x^2}(4x^2-2).\]
La figura\(\PageIndex{8}\) muestra una gráfica de\(f"(x)\) on\([0,1]\). Es claro que el mayor valor de\(f"\), en valor absoluto, es 2. Así dejamos\(M=2\) y aplicamos la fórmula de error del Teorema\(\PageIndex{1}\).
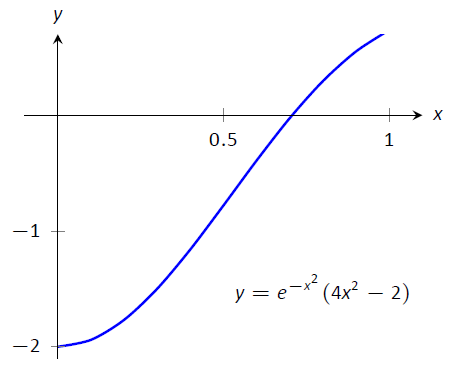
Figura\(\PageIndex{9}\): Graficando\(f"(x)\) en Ejemplo\(\PageIndex{7}\) para ayudar a establecer límites de error.
$$E_T =\ frac {(1-0) ^3} {12\ cdot 5^2}\ cdot 2 = 0.00\ overline {6}.\]
Nuestra fórmula de estimación de errores establece que nuestra aproximación de 0.7445 encontrada en Ejemplo\(\PageIndex{3}\) está dentro de 0.0067 de la respuesta correcta, de ahí que sepamos que
$$0.7445-0.0067 = .7378\ leq\ int_0^1e^ {-x^2}\ dx\ leq 0.7512 = 0.7445 + 0.0067.\]
Anteriormente habíamos calculado la respuesta exacta, correcta a 4 decimales, para ser 0.7468, afirmando la validez del Teorema\(\PageIndex{1}\).
La Regla de Simpson con\(n=4\):
Comenzamos por computar la\(4^\text{th}\) derivada de\(f(x) = e^{-x^2}\):
$$f\, ^ {(4)} (x) = e^ {-x^2} (16x^4-48x^2+12).\]
La figura\(\PageIndex{9}\) muestra una gráfica de\(f\,^{(4)}(x)\) on\([0,1]\). Es claro que el mayor valor de\(f\,^{(4)}\), en valor absoluto, es 12. Así dejamos\(M=12\) y aplicamos la fórmula de error del Teorema\(\PageIndex{1}\).
$$e_s =\ frac {(1-0) ^5} {180\ cdot 4^4}\ cdot 12 = 0.00026.\]
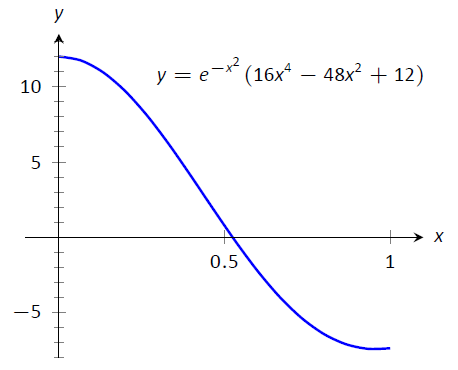
Figura\(\PageIndex{10}\): Graficando\(f\,^{(4)}(x)\) en Ejemplo\(\PageIndex{7}\) para ayudar a establecer límites de error.
Nuestra fórmula de estimación de errores establece que nuestra aproximación de\(0.7468\overline{3}\) encontrado en Ejemplo\(\PageIndex{5}\) está dentro de 0.00026 de la respuesta correcta, de ahí que sepamos que
$$0.74683-0.00026 = .74657\ leq\ int_0^1e^ {-x^2}\ dx\ leq 0.74709 = 0.74683 + 0.00026.\]
Una vez más afirmamos la validez del Teorema\(\PageIndex{1}\).
Al inicio de esta sección mencionamos dos situaciones principales donde la integración numérica era deseable. Hemos considerado el caso en el que no se puede computar una antiderivada del integrando. Ahora investigamos la situación en la que no se conoce el integrando. Esta es, de hecho, la aplicación más utilizada de los métodos de Integración Numérica. “La mayor parte del tiempo” observamos el comportamiento pero no conocemos “la” función que lo describe. En su lugar, recopilamos datos sobre el comportamiento y hacemos aproximaciones basadas en estos datos. Esto lo demostramos en un ejemplo.
Ejemplo\(\PageIndex{8}\): Approximating distance traveled
Una de las autoras condujo a su hija a casa desde la escuela mientras ella registraba su velocidad cada 30 segundos. Los datos se dan en la Tabla\(\PageIndex{5}\). Aproximar la distancia que recorrieron.
Solución
Recordemos que al integrar una función de velocidad obtenemos la distancia recorrida. Tenemos información sobre\(v(t)\); usaremos la Regla de Simpson para aproximar\(\int_a^b v(t)\ dt.\)
El aspecto más difícil de este problema es convertir los datos dados en la forma en la que necesitamos que esté. La velocidad se mide en millas por hora, mientras que el tiempo se mide en incrementos de 30 segundos.
| 0 | 0 |
| 1 | 25 |
| 2 | 22 |
| 3 | 19 |
| 4 | 39 |
| 5 | 0 |
| 6 | 43 |
| 7 | 59 |
| 8 | 54 |
| 9 | 51 |
| 10 | 43 |
| 11 | 35 |
| 12 | 40 |
| 13 | 43 |
| 14 | 30 |
| 15 | 0 |
| 16 | 0 |
| 17 | 28 |
| 18 | 40 |
| 19 | 42 |
| 20 | 40 |
| 21 | 39 |
| 22 | 40 |
| 23 | 23 |
| 24 | 0 |
Tenemos que computar\(\ dx = (b-a)/n\). Claramente,\(n=24\). ¿Qué son\(a\) y\(b\)? Desde que empezamos por el tiempo\(t=0\), tenemos eso\(a=0\). El tiempo final registrado llegó después de 24 periodos de 30 segundos, que es de 12 minutos o 1/5 de hora. Así tenemos
$$\ dx =\ frac {b-a} {n} =\ frac {1/5-0} {24} =\ frac1 {120};\ quad\ frac {\ dx} {3} =\ frac {1} {360}.\]
Así, la distancia recorrida es aproximadamente:
\ [\ begin {align*}\ int_0^ {0.2} v (t)\ dt &\ approx\ frac {1} {360}\ Grande [f (x_1) +4f (x_2) + 2f (x_3) +\ cdots + 4f (x_n) +f (x_ {n+1})\ Grande]\\
&=\ frac {1} 360}\ Grande [0+4\ cdot25+2\ cdot 22 +\ cdots + 2\ cdot40+4\ cdot 23 + 0\ Grande]\\ &\ aprox 6.2167\\ texto {millas.} \ end {alinear*}\]
Nos aproximamos al autor condujo 6.2 millas. (Porque estamos seguros que el lector quiere saber, el odómetro del autor registró la distancia como aproximadamente 6.05 millas).
Iniciamos este capítulo aprendiendo sobre antiderivados e integrales indefinidas. Entonces parecíamos cambiar de enfoque al observar áreas entre la gráfica de una función y el\(x\) eje -eje. Definimos estas áreas como la integral definida de la función, utilizando una notación muy similar a la notación de la integral indefinida. El Teorema Fundamental del Cálculo vinculó estos dos conceptos aparentemente separados: podemos encontrar áreas bajo una curva, es decir, podemos evaluar una integral definida, utilizando antiderivados.
Terminamos el capítulo señalando que los antiderivados son a veces más que difíciles de encontrar: son imposibles. Por lo tanto desarrollamos técnicas numéricas que nos dieron buenas aproximaciones de integrales definidas.
Utilizamos la integral definida para calcular áreas, y también para calcular desplazamientos y distancias recorridas. Hay mucho más que podemos hacer que eso. En el Capítulo 7 veremos más aplicaciones de la integral definida. Antes de eso, en el Capítulo 6 aprenderemos técnicas avanzadas de integración, análogas a reglas de aprendizaje como el Producto, el Cociente y las Reglas de Cadena de diferenciación.