5.4: El teorema fundamental del cálculo

Dejar$f(t)$ ser una función continua definida en$[a,b]$. La integral definitiva$\displaystyle \int_a^b f(x)\,dx$ es el “área bajo$f$” en$[a,b]$. Podemos convertir este concepto en una función dejando variar el límite superior (o inferior).

Vamos$\displaystyle F(x) = \int_a^x f(t) \,dt$. Calcula el área bajo$f$ on$[a,x]$ como se ilustra en la Figura$\PageIndex{1}$. Podemos estudiar esta función utilizando nuestro conocimiento de la integral definida. Por ejemplo,$F(a)=0$ ya que$\displaystyle \int_a^af(t) \,dt=0$.

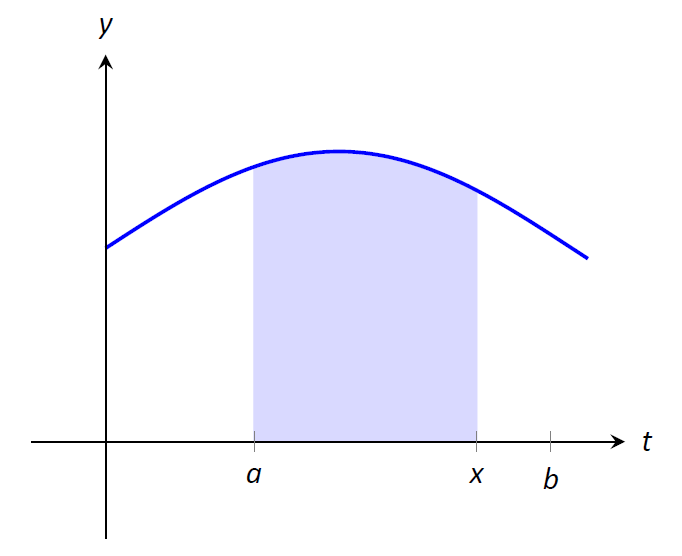
Figura$\PageIndex{1}$: El área de la región sombreada es$\displaystyle F(x) = \int_a^x f(t) \,dt$.

También podemos aplicar ideas de cálculo a$F(x)$; en particular, podemos calcular su derivada. Si bien esto puede parecer algo inocuo, tiene implicaciones de largo alcance, como lo demuestra el hecho de que el resultado se da como un teorema importante.

Teorema$\PageIndex{1}$: The Fundamental Theorem of Calculus, Part 1

Dejar$f$ ser continuo$[a,b]$ y dejar$\displaystyle F(x) = \int_a^x f(t) \,dt$. Entonces$F$ es una función diferenciable en$(a,b)$, y

$$F'(x)=f(x).$$

Inicialmente esto parece sencillo, como se demuestra en el siguiente ejemplo.

Ejemplo$\PageIndex{1}$: Using the Fundamental Theorem of Calculus, Part 1

Vamos$\displaystyle F(x) = \int_{-5}^x (t^2+\sin t) \,dt$. ¿Qué es$F'(x)$?}

Solución

Utilizando el Teorema Fundamental del Cálculo, tenemos$F'(x) = x^2+\sin x$.

Este sencillo ejemplo revela algo increíble: ¡$F(x)$es un antiderivado de$x^2+\sin x$! Por lo tanto,$F(x) = \frac13x^3-\cos x+C$ por algún valor de$C$. (Podemos encontrar$C$, pero generalmente no nos importa. Eso lo sabemos$F(-5)=0$, lo que nos permite computar$C$. En este caso,$C=\cos(-5)+\frac{125}3$.)

Hemos hecho más que encontrar una forma complicada de computar un antiderivado. Considere una función$f$ definida en un intervalo abierto que contiene$a$,$b$ y$c$. Supongamos que queremos calcular$\displaystyle \int_a^b f(t) \,dt$. Primero, vamos$\displaystyle F(x) = \int_c^x f(t)\,dt$. Usando las propiedades de la integral definida que se encuentran en el Teorema 5.2.1, sabemos

$$\begin{align}\int_a^b f(t) \,dt&= \int_a^c f(t) \,dt+ \int_c^b f(t) \,dt \\ &= -\int_c^a f(t) \,dt + \int_c^b f(t) \,dt \\ &=-F(a) + F(b)\\&= F(b) - F(a). \end{align}$$

Ahora vemos cómo se relacionan las integrales indefinidas y las integrales definidas: ¡podemos evaluar una integral definida usando antiderivados! Esta es la segunda parte del Teorema Fundamental del Cálculo.

Teorema$\PageIndex{2}$: The Fundamental Theorem of Calculus, Part 2

Dejar$f$ ser continuo$[a,b]$ y dejar que$F$ sea cualquier antiderivado de$f$. Entonces

$$\int_a^b f(x)\,dx = F(b) - F(a).$$

Ejemplo$\PageIndex{2}$: Using the Fundamental Theorem of Calculus, Part 2

Pasamos mucho tiempo en la sección anterior estudiando$\int_0^4(4x-x^2)\,dx$. Utilizando el Teorema Fundamental del Cálculo, evaluar esta integral definida.

Solución

Necesitamos un antiderivado de$f(x)=4x-x^2$. Todos los antiderivados de$f$ tienen la forma$F(x) = 2x^2-\frac13x^3+C$; por simplicidad, elija$C=0$.

El teorema fundamental de los estados de cálculo

$$\int_0^4(4x-x^2)\,dx = F(4)-F(0) = \big(2(4)^2-\frac134^3\big)-\big(0-0\big) = 32-\frac{64}3 = 32/3.$$

Esta es la misma respuesta que obtuvimos usando límites en el apartado anterior, solo con mucho menos trabajo.

Notación: A menudo se utiliza una notación especial en el proceso de evaluación de integrales definidas utilizando el Teorema Fundamental del Cálculo. En lugar de escribir explícitamente$F(b)-F(a)$,$F(x)\Big|_a^b$ se utiliza la notación. Así la solución al Ejemplo se$\PageIndex{2}$ escribiría como:

$$\int_0^4(4x-x^2)\,dx = \left.\left(2x^2-\frac13x^3\right)\right|_0^4 = \big(2(4)^2-\frac134^3\big)-\big(0-0\big) = 32/3.$$

La Constante$C$: Cualquier antiderivado se$F(x)$ puede elegir cuando se utiliza el Teorema Fundamental del Cálculo para evaluar una integral definida, es decir, cualquier valor de$C$ puede ser escogido. La constante siempre cancela fuera de la expresión al evaluar$F(b)-F(a)$, por lo que no importa qué valor se escoja. Siendo este el caso, bien podríamos dejar$C=0$.

Ejemplo$\PageIndex{3}$: Using the Fundamental Theorem of Calculus, Part 2

Evaluar las siguientes integrales definidas.

$$1.\ \int_{-2}^2 x^3\,dx \quad 2.\ \int_0^\pi \sin x\,dx \qquad 3.\ \int_0^5 e^t \,dt \qquad 4.\ \int_4^9 \sqrt{u}\ du\qquad 5.\ \int_1^5 2\,dx$$

Solución

1. $\displaystyle \int_{-2}^2 x^3\,dx = \left.\frac14x^4\right|_{-2}^2 = \left(\frac142^4\right) - \left(\frac14(-2)^4\right) = 0.$
2. $\displaystyle \int_0^\pi \sin x\,dx = -\cos x\Big|_0^\pi = -\cos \pi- \big(-\cos 0\big) = 1+1=2.$
   (Esto es interesante; dice que el área bajo una “joroba” de una curva sinusoidal es 2.)
3. $\displaystyle \int_0^5e^t \,dt = e^t\Big|_0^5 = e^5 - e^0 = e^5-1 \approx 147.41.$
4. $\displaystyle \int_4^9 \sqrt{u}\ du = \int_4^9 u^\frac12\ du = \left.\frac23u^\frac32\right|_4^9 = \frac23\left(9^\frac32-4^\frac32\right) = \frac23\big(27-8\big) =\frac{38}3.$
5. $\displaystyle \int_1^5 2\,dx = 2x\Big|_1^5 = 2(5)-2=2(5-1)=8.$

Esta integral es interesante; el integrando es una función constante, de ahí que estemos encontrando el área de un rectángulo con ancho$(5-1)=4$ y alto 2. Observe cómo la evaluación de la integral definitiva condujo a$2(4)=8$.

En general, si$c$ es una constante, entonces$\displaystyle \int_a^b c\,dx = c(b-a)$.

Entendiendo el Movimiento con el Teorema Fundamental del Cálculo

Establecimos, comenzando con la Idea Clave 1, que la derivada de una función de posición es una función de velocidad, y la derivada de una función de velocidad es una función de aceleración. Ahora considere integrales definidas de funciones de velocidad y aceleración. Específicamente, si$v(t)$ es una función de velocidad, ¿qué$\displaystyle \int_a^b v(t) \,dt$ significa?

El Teorema Fundamental del Cálculo establece que

$$\int_a^b v(t) \,dt = V(b) - V(a),$$

donde$V(t)$ es cualquier antiderivado de$v(t)$. Dado que$v(t)$ es una función de velocidad,$V(t)$ debe ser una función de posición, y$V(b) - V(a)$ mide un cambio de posición, o desplazamiento.

Ejemplo$\PageIndex{4}$: Finding displacement

Se lanza una pelota recta hacia arriba con velocidad dada por$v(t) = -32t+20$ pies/s, donde$t$ se mide en segundos. Encontrar e interpretar,$\displaystyle \int_0^1 v(t) \,dt.$}

Solución

Usando el Teorema Fundamental del Cálculo, tenemos

$$\begin{align} \int_0^1 v(t) \,dt &= \int_0^1 (-32t+20) \,dt \\ &= -16t^2 + 20t\Big|_0^1 \\ &= 4. \end{align}$$

De esta manera, si una pelota es arrojada hacia arriba al aire con velocidad$v(t) = -32t+20$, la altura de la pelota, 1 segundo después, será de 4 pies por encima de la altura inicial. (Tenga en cuenta que la pelota ha viajado mucho más lejos. Ha subido a su pico y está cayendo, pero la diferencia entre su altura a$t=0$ y$t=1$ es de 4 pies.

Integrar una función de tasa de cambio da cambio total. La velocidad es la tasa de cambio de posición; la velocidad de integración da el cambio total de posición, es decir, desplazamiento.

La integración de una función de velocidad da un resultado similar, aunque diferente. La velocidad también es la tasa de cambio de posición, pero no tiene en cuenta la dirección. Por lo que la integración de una función de velocidad da un cambio total de posición, sin la posibilidad de “cambio de posición negativo”. De ahí que la integral de una función de velocidad da la distancia recorrida.

Como la aceleración es la tasa de cambio de velocidad, la integración de una función de aceleración da un cambio total en la velocidad. No tenemos un término simple para esto análogo al desplazamiento. Si$a(t) = 5 \text{ miles}/\text{h}^2$ y$t$ se mide en horas, entonces

$$\int_0^3 a(t) \,dt = 15$$

significa que la velocidad ha aumentado en 15 m/h de$t=0$ a$t=3$.

El teorema fundamental del cálculo y la regla de la cadena

Parte 1 del Teorema Fundamental del Cálculo (FTC) establece que dado$\displaystyle F(x) = \int_a^x f(t) \,dt$,$F'(x) = f(x)$. Usando otra notación,$\frac{d}{\,dx}\big(F(x)\big) = f(x)$. Si bien acabamos de practicar la evaluación de integrales definidas, a veces es imposible encontrar antiderivados y necesitamos apoyarnos en otras técnicas para aproximar el valor de una integral definida. Las funciones escritas como$\displaystyle F(x) = \int_a^x f(t) \,dt$ son útiles en tales situaciones.

Puede ser de mayor utilidad componer tal función con otra. Como ejemplo, podemos componer$F(x)$ con$g(x)$ para obtener

$$F\big(g(x)\big) = \int_a^{g(x)} f(t) \,dt.$$

¿Cuál es la derivada de tal función? La regla de la cadena se puede emplear para declarar

$$\frac{d}{\,dx}\Big(F\big(g(x)\big)\Big) = F'\big(g(x)\big)g'(x) = f\big(g(x)\big)g'(x).$$

Un ejemplo nos ayudará a entender esto.

Ejemplo$\PageIndex{4}$: The FTC, Part 1, and the Chain Rule

Encuentra la derivada de$\displaystyle F(x) = \int_2^{x^2} \ln t \,dt$.

Solución

Podemos ver$F(x)$ como siendo la función$\displaystyle G(x) = \int_2^x \ln t \,dt$ compuesta con$g(x) = x^2$; es decir,$F(x) = G\big(g(x)\big)$. El Teorema Fundamental del Cálculo afirma que$G'(x) = \ln x$. La Regla de la Cadena nos da

$$\begin{align} F'(x) &= G'\big(g(x)\big) g'(x) \\ &= \ln (g(x)) g'(x) \\ &= \ln (x^2) 2x \\ &=2x\ln x^2 \end{align}$$

Normalmente, los pasos que definen$G(x)$ y$g(x)$ se saltan.

Practica esto una vez más.

Ejemplo$\PageIndex{5}$: The FTC, Part 1, and the Chain Rule

Encuentra la derivada de$\displaystyle F(x) = \int_{\cos x}^5 t^3 \,dt.$

Solución

Tenga en cuenta que$\displaystyle F(x) = -\int_5^{\cos x} t^3 \,dt$. Visto de esta manera, la derivada de$F$ es sencilla:

$$F'(x) = \sin x \cos^3 x.$$

Área entre curvas

Considerar funciones continuas$f(x)$ y$g(x)$ definidas en$[a,b]$, donde$f(x) \geq g(x)$ para todos$x$ en$[a,b]$, como se demuestra en la Figura$\PageIndex{2}$. ¿Cuál es el área de la región sombreada delimitada por las dos curvas$[a,b]$?

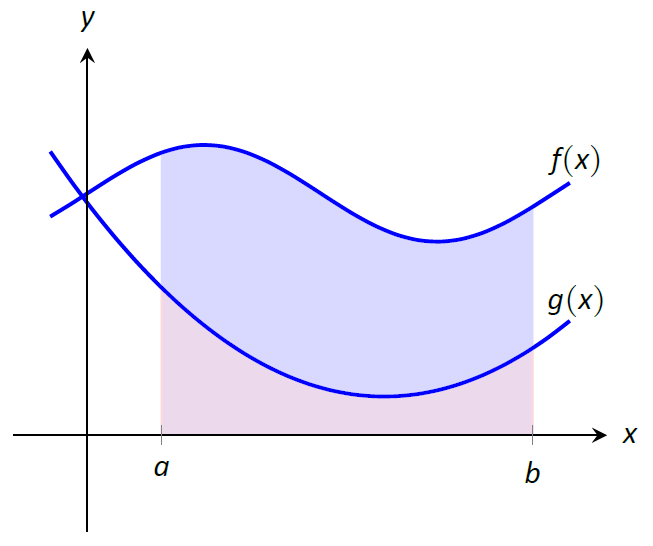
Figura$\PageIndex{2}$: Encontrar el área delimitada por dos funciones en un intervalo; se encuentra restando el área debajo$g$ del área inferior$f$.

El área se puede encontrar reconociendo que esta área es “el área debajo$f$$-$ del área debajo”$g$. Usando notación matemática, el área es

$$\int_a^b f(x)\,dx - \int_a^b g(x)\,dx.$$

Las propiedades de la integral definida nos permiten simplificar esta expresión para

$$\int_a^b\big(f(x) - g(x)\big)\,dx.$$

Teorema$\PageIndex{3}$: Area Between Curves

Dejar$f(x)$ y$g(x)$ ser funciones continuas definidas sobre$[a,b]$ dónde$f(x)\geq g(x)$ para todos$x$ en$[a,b]$. El área de la región delimitada por las curvas$y=f(x)$,$y=g(x)$ y las líneas$x=a$ y$x=b$ es

$$\int_a^b \big(f(x)-g(x)\big)\,dx.$$

Ejemplo$\PageIndex{6}$: Finding area between curves

Encuentra el área de la región encerrada por$y=x^2+x-5$ y$y=3x-2$.

Solución

Ayudará a bosquejar estas dos funciones, como se hace en la Figura$\PageIndex{3}$.

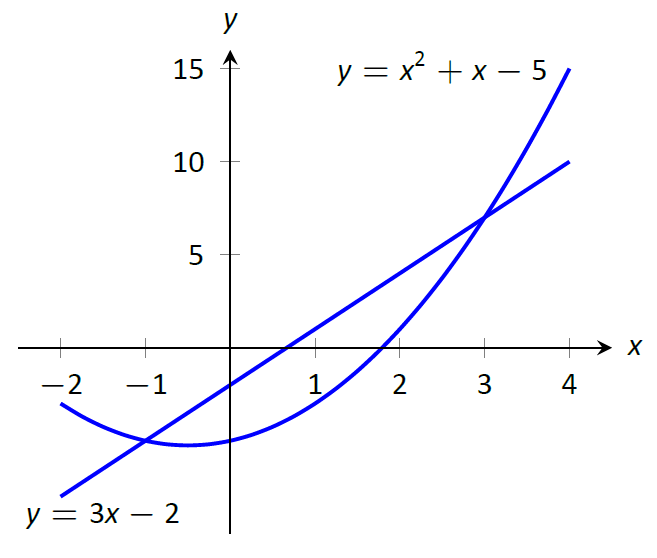
Figura$\PageIndex{3}$: Croquizar la región encerrada por$y=x^2+x-5$ y$y=3x-2$ en Ejemplo$\PageIndex{6}$

La región cuya zona buscamos está completamente delimitada por estas dos funciones; parecen cruzarse en$x=-1$ y$x=3$. Para verificar, configurar$x^2+x-5=3x-2$ y resolver$x$:

$$\begin{align} x^2+x-5 &= 3x-2 \\ (x^2+x-5) - (3x-2) &= 0\\ x^2-2x-3 &= 0\\ (x-3)(x+1) &= 0\\ x&=-1,\ 3. \end{align}$$

Siguiendo el teorema$\PageIndex{3}$, el área es

$$\begin{align}\int_{-1}^3\big(3x-2 -(x^2+x-5)\big)\,dx &= \int_{-1}^3 (-x^2+2x+3)\,dx \\ &=\left.\left(-\frac13x^3+x^2+3x\right)\right|_{-1}^3 \\ &=-\frac13(27)+9+9-\left(\frac13+1-3\right)\\ &= 10\frac23 = 10.\overline{6} \end{align}$$

El teorema del valor medio y el valor promedio

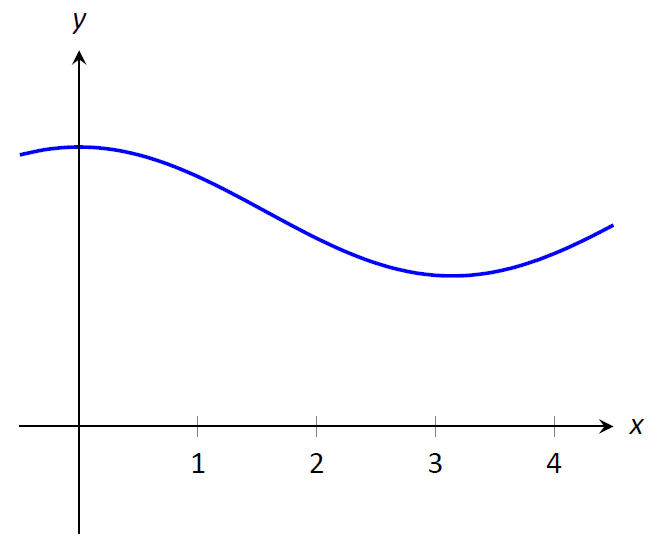
Figura$\PageIndex{4}$: Gráfica de una función$f$ para introducir el Teorema del Valor Medio.

Considera la gráfica de una función$f$ en la Figura$\PageIndex{4}$ y el área definida por$\displaystyle \int_1^4 f(x)\,dx$. En la Figura se dibujan tres rectángulos$\PageIndex{5}$; en (a), la altura del rectángulo es mayor que$f$ sobre$[1,4]$, de ahí que el área de este rectángulo sea mayor que$\displaystyle \int_0^4 f(x)\,dx$.

En (b), la altura del rectángulo es menor que$f$ on$[1,4]$, de ahí que el área de este rectángulo sea menor que$\displaystyle \int_1^4 f(x)\,dx$.

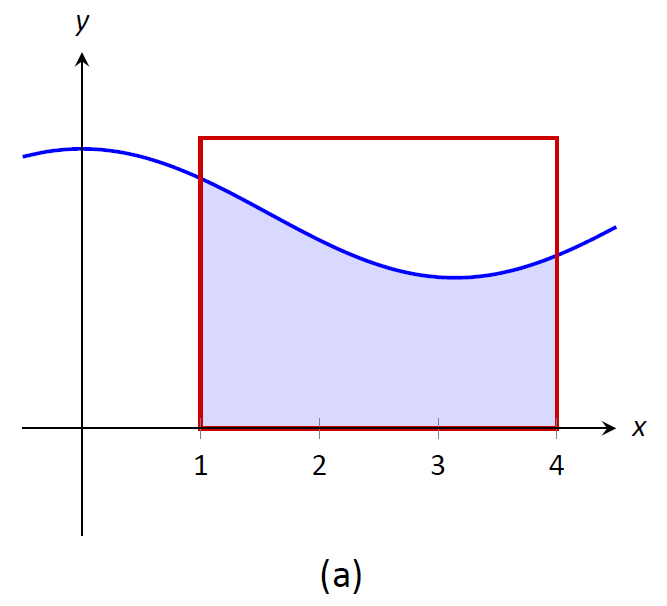
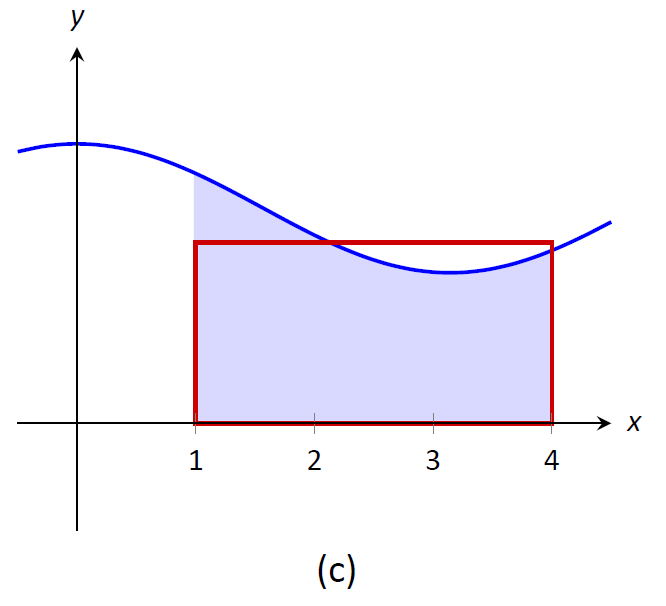
Figura$\PageIndex{5}$: Los rectángulos de diferente tamaño dan límites superior e inferior$\displaystyle \int_1^4 f(x)\,dx$; el último rectángulo coincide exactamente con el área.

Finalmente, en (c) la altura del rectángulo es tal que el área del rectángulo es exactamente la de$\displaystyle \int_0^4 f(x)\,dx$. Dado que los rectángulos que son “demasiado grandes”, como en (a), y los rectángulos que son “demasiado pequeños”, como en (b), dan áreas mayores o menores que$\displaystyle \int_1^4 f(x)\,dx$, tiene sentido que haya un rectángulo, cuya parte superior se cruza en$f(x)$ algún lugar de$[1,4]$, cuya área es exactamente la de la integral definida.

Declaramos esta idea formalmente en un teorema.

Teorema$\PageIndex{4}$: The Mean Value Theorem of Integration

Dejar$f$ ser continuo en$[a,b]$. Existe un valor$c$ en$[a,b]$ tal que

$$\int_a^bf(x)\,dx = f(c)(b-a).$$

Esta es una declaración existencial;$c$ existe, pero no proporcionamos un método para encontrarla. El teorema$\PageIndex{4}$ está directamente conectado con el Teorema del Valor Medio de la Diferenciación, dado como Teorema 3.2.1; dejamos que el lector vea cómo.

Demostramos los principios involucrados en esta versión del Teorema del Valor Medio en el siguiente ejemplo.

Ejemplo$\PageIndex{7}$: Using the Mean Value Theorem

Considerar$\displaystyle \int_0^\pi \sin x\,dx$. Encontrar un valor$c$ garantizado por el Teorema del Valor Medio.

Solución

Primero tenemos que evaluar$\displaystyle \int_0^\pi \sin x\,dx$. (Esto se hizo anteriormente en el Ejemplo$\PageIndex{3}$)

$$\int_0^\pi\sin x\,dx = -\cos x \Big|_0^\pi = 2.$$

Así buscamos un valor$c$ en$[0,\pi]$ tal que$\pi\sin c =2$.

$$\pi\sin c = 2\ \ \Rightarrow\ \ \sin c = 2/\pi\ \ \Rightarrow\ \ c = \arcsin(2/\pi) \approx 0.69.$$

Figura$\PageIndex{6}$: Una gráfica de$y=\sin x$ on$[0,\pi]$ y el rectángulo garantizado por el Teorema del Valor Medio.

En la Figura$\PageIndex{6}$$\sin x$ se esboza junto con un rectángulo con altura$\sin (0.69)$. El área del rectángulo es la misma que el área debajo$\sin x$ de$[0,\pi]$.

Dejemos$f$ ser una función en$[a,b]$ con$c$ tal que$\displaystyle f(c)(b-a) = \int_a^bf(x)\,dx$. Considerar$\displaystyle \int_a^b\big(f(x)-f(c)\big)\,dx$:

$$\begin{align} \int_a^b\big(f(x)-f(c)\big)\,dx &= \int_a^b f(x) - \int_a^b f(c)\,dx\\ &= f(c)(b-a) - f(c)(b-a) \\ &= 0. \end{align}$$

Cuando$f(x)$ se desplaza por$-f(c)$, la cantidad de área por debajo$f$ del$x$ eje -on$[a,b]$ es la misma que la cantidad de área debajo del$x$ eje -arriba$f$; ver Figura$\PageIndex{7}$ para una ilustración de esto. En este sentido, podemos decir que$f(c)$ es el valor promedio de$f$ on$[a,b]$.

Figura$\PageIndex{7}$: A la izquierda, una gráfica de$y=f(x)$ y el rectángulo garantizado por el Teorema del Valor Medio. A la derecha,$y=f(x)$ se desplaza hacia abajo por$f(c)$; el “área bajo la curva” resultante es 0.

El valor$f(c)$ es el valor promedio en otro sentido. Primero, reconocer que el Teorema del Valor Medio puede ser reescrito como

$$f(c) = \frac{1}{b-a}\int_a^b f(x)\,dx,$$

por algún valor de$c$ in$[a,b]$. A continuación, particione el intervalo$[a,b]$ en subintervalos$n$ igualmente espaciados$a=x_1 < x_2 < \ldots < x_{n+1}=b$ y elija cualquiera$c_i$ en$[x_i,x_{i+1}]$. El promedio de los números$f(c_1)$,$f(c_2)$,$\ldots$,$f(c_n)$ es:

$$\frac1n\Big(f(c_1) + f(c_2) + \ldots + f(c_n)\Big) = \frac1n\sum_{i=1}^n f(c_i).$$

Multiplica esta última expresión por 1 en forma de$\frac{(b-a)}{(b-a)}$:

$$\begin{align} \frac1n\sum_{i=1}^n f(c_i) &= \sum_{i=1}^n f(c_i)\frac1n \\ &= \sum_{i=1}^n f(c_i)\frac1n \frac{(b-a)}{(b-a)} \\ &=\frac{1}{b-a} \sum_{i=1}^n f(c_i)\,\Delta x\quad \text{(where $\Delta x = (b-a)/n$)} \end{align}$$

Ahora toma el límite como$n\to\infty$:

$$\lim_{n\to\infty} \frac{1}{b-a} \sum_{i=1}^n f(c_i)\,\Delta x\quad = \quad \frac{1}{b-a} \int_a^b f(x)\,dx\quad = \quad f(c).$$

Esto nos dice esto: cuando evaluamos$f$ en puntos$n$ (algo) igualmente espaciados en$[a,b]$, el valor promedio de estas muestras es$f(c)$ como$n\to\infty$.

Esto nos lleva a una definición.

Definición$\PageIndex{1}$: The Average Value of $f$ on $[a,b]$

Dejar$f$ ser continuo en$[a,b]$. El valor promedio de$f$ on$[a,b]$ es$f(c)$, donde$c$ es un valor en$[a,b]$ garantizado por el Teorema del Valor Medio. Es decir,

\[\text{Average Value of $f$ on $[a,b]$} = \frac{1}{b-a}\int_a^b f(x)\,dx.\]

Una aplicación de esta definición se da en el siguiente ejemplo.

Ejemplo$\PageIndex{8}$: Finding the average value of a function

Un objeto se mueve hacia adelante y hacia atrás a lo largo de una línea recta con una velocidad dada por$v(t) = (t-1)^2$ on$[0,3]$, donde$t$ se mide en segundos y$v(t)$ se mide en pies/s.

¿Cuál es la velocidad promedio del objeto?

Solución

Por nuestra definición, la velocidad promedio es:

$$\frac{1}{3-0}\int_0^3 (t-1)^2 \,dt =\frac13 \int_0^3 \big(t^2-2t+1\big) \,dt = \left.\frac13\left(\frac13t^3-t^2+t\right)\right|_0^3 = 1\text{ ft/s}.$$

Podemos entender el ejemplo anterior a través de una situación más sencilla. Supongamos que manejó 100 millas en 2 horas. ¿Cuál fue tu velocidad promedio? La respuesta es simple:$\text{displacement}/\text{time} = 100 \;\text{miles}/2\;\text{hours} = 50 mph$.

¿Cuál fue el desplazamiento del objeto en Ejemplo$\PageIndex{8}$? Calculamos esto integrando su función de velocidad:$\displaystyle \int_0^3 (t-1)^2 \,dt = 3$ ft. Su posición final fue a 3 pies de su posición inicial después de 3 segundos: su velocidad promedio fue de 1 pies/s.

Esta sección ha sentado las bases para que sigan muchas grandes matemáticas. La lección más importante es esta: las integrales definidas pueden evaluarse usando antiderivados. Dado que la sección anterior establecía que las integrales definidas son el límite de las sumas de Riemann, posteriormente podemos crear sumas de Riemann a valores aproximados distintos del “área bajo la curva”, convertir las sumas en integrales definidas, luego evaluarlas usando el Teorema Fundamental del Cálculo. Esto nos permitirá calcular el trabajo realizado por una fuerza variable, el volumen de ciertos sólidos, la longitud del arco de las curvas, y más.

La desventaja es esta: en términos generales, los antiderivados informáticos son mucho más difíciles que los derivados informáticos. El siguiente capítulo está dedicado a las técnicas de búsqueda de antiderivados para que se pueda evaluar una amplia variedad de integrales definidas. Antes de eso, la siguiente sección explora técnicas de aproximación al valor de integrales definidas más allá del uso de las Reglas de Mano Izquierda, Mano Derecha y Punto Medio.

Colaboradores y Atribuciones

• Template:ContribApexCalc
• Template:ContribMarshall