5.1: Aproximación de áreas

Última actualización
Guardar como PDF

Page ID: 116201

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Utilice la notación sigma (suma) para calcular sumas y potencias de enteros.
Utilice la suma de áreas rectangulares para aproximar el área bajo una curva.
Utilice las sumas de Riemann para aproximar el área.

Arquímedes estaba fascinado con el cálculo de las áreas de diversas formas, es decir, la cantidad de espacio encerrado por la forma. Utilizó un proceso que ha llegado a conocerse como el método de agotamiento, que utilizó formas cada vez más pequeñas, cuyas áreas podrían calcularse exactamente, para llenar una región irregular y con ello obtener aproximaciones cada vez más cercanas al área total. En este proceso, un área delimitada por curvas se rellena con rectángulos, triángulos y formas con fórmulas de área exactas. Estas áreas se suman luego para aproximarse al área de la región curva.

En esta sección, desarrollamos técnicas para aproximar el área entre una curva, definida por una función$f(x),$ y el eje x en un intervalo cerrado$[a,b].$ Al igual que Arquímedes, primero aproximamos el área bajo la curva utilizando formas de área conocida (es decir, rectángulos). Mediante el uso de rectángulos cada vez más pequeños, conseguimos aproximaciones cada vez más cercanas al área. Tomar un límite nos permite calcular el área exacta bajo la curva.

Empecemos por introducir alguna notación para facilitar los cálculos. Luego consideramos el caso cuando$f(x)$ es continuo y no negativo. Posteriormente en el capítulo, relajamos algunas de estas restricciones y desarrollamos técnicas que aplican en casos más generales.

Notación Sigma (suma)

Como se mencionó, utilizaremos formas de área conocida para aproximar el área de una región irregular delimitada por curvas. Este proceso a menudo requiere sumar largas cadenas de números. Para que sea más fácil anotar estas sumas largas, observamos aquí alguna notación nueva, llamada notación sigma (también conocida como notación de suma). La letra mayúscula griega$Σ$, sigma, se utiliza para expresar sumas largas de valores en forma compacta. Por ejemplo, si queremos sumar todos los enteros del 1 al 20 sin notación sigma, tenemos que escribir

\[1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+18+19+20. \nonumber \]

Probablemente podríamos omitir escribir un par de términos y escribir

\[1+2+3+4+⋯+19+20, \nonumber \]

que es mejor, pero sigue siendo engorroso. Con notación sigma, escribimos esta suma como

\[\sum_{i=1}^{20}i \nonumber \]

que es mucho más compacto. Típicamente, la notación sigma se presenta en la forma

\[\sum_{i=1}^{n}a_i \nonumber \]

donde$a_i$ describe los términos a agregar, y el$i$ se llama el$index$. Cada término se evalúa, luego sumamos todos los valores, comenzando con el valor cuándo$i=1$ y terminando con el valor cuando$i=n.$ Por ejemplo, una expresión como$\displaystyle \sum_{i=2}^{7}s_i$ se interpreta como$s_2+s_3+s_4+s_5+s_6+s_7$. Tenga en cuenta que el índice se utiliza únicamente para realizar un seguimiento de los términos a agregar; no tiene en cuenta en el cálculo de la suma en sí. Por lo tanto, el índice se llama una variable ficticia. Podemos usar cualquier letra que queramos para el índice. Por lo general, los matemáticos utilizan$i, \,j, \,k, \,m$, y$n$ para los índices.

Probemos un par de ejemplos de uso de notación sigma.

Ejemplo$\PageIndex{1}$: Using Sigma Notation

Escribir en notación sigma y evaluar la suma de términos$3^i$ para$i=1,2,3,4,5.$
Escribe la suma en notación sigma:

\[1+\dfrac{1}{4}+\dfrac{1}{9}+\dfrac{1}{16}+\dfrac{1}{25}. \nonumber \]

Solución

Escribir\[\sum_{i=1}^{5}3^i=3+3^2+3^3+3^4+3^5=363. \nonumber \]
El denominador de cada término es un cuadrado perfecto. Usando notación sigma, esta suma se puede escribir como$\displaystyle \sum_{i=1}^5\dfrac{1}{i^2}$.

Ejercicio$\PageIndex{1}$

Escribir en notación sigma y evaluar la suma de términos$2^i$ para$i=3,4,5,6.$

Pista: Utilice los pasos de resolución de Ejemplo$\PageIndex{1}$ como guía.

Contestar: $\displaystyle \sum_{i=3}^{6}2^i=2^3+2^4+2^5+2^6=120$

Las propiedades asociadas al proceso de suma se dan en la siguiente regla.

Regla: Propiedades de la notación Sigma

Dejar$a_1,a_2,…,a_n$ y$b_1,b_2,…,b_n$ representar dos secuencias de términos y dejar$c$ ser una constante. Las siguientes propiedades se mantienen para todos los enteros positivos$n$ y para los enteros$m$, con$1≤m≤n.$

$\displaystyle \sum_{i=1}^n c=nc$
$\displaystyle \sum_{i=1}^n ca_i=c\sum_{i=1}^na_i$
$\displaystyle \sum_{i=1}^n(a_i+b_i)=\sum_{i=1}^na_i+\sum_{i=1}^nb_i$
$\displaystyle \sum_{i=1}^n(a_i−b_i)=\sum_{i=1}^na_i−\sum_{i=1}^nb_i$
$\displaystyle \sum_{i=1}^na_i=\sum_{i=1}^ma_i+\sum_{i=m+1}^na_i$

Prueba

Aquí probamos propiedades (ii.) y (iii.) y dejamos constancia de las otras propiedades a los Ejercicios.

(ii.) Tenemos

\[\sum_{i=1}^nca_i=ca_1+ca_2+ca_3+⋯+ca_n=c(a_1+a_2+a_3+⋯+a_n)=c\sum_{i=1}^na_i. \nonumber \]

(iii.) Tenemos

\[ \begin{align} \sum_{i=1}^{n}(a_i+b_i) &=(a_1+b_1)+(a_2+b_2)+(a_3+b_3)+⋯+(a_n+b_n) \\[4pt] &=(a_1+a_2+a_3+⋯+a_n)+(b_1+b_2+b_3+⋯+b_n) \\[4pt] &=\sum_{i=1}^na_i+\sum_{i=1}^nb_i. \end {align} \nonumber \]

□

Algunas fórmulas más para las funciones que se encuentran con frecuencia simplifican aún más el proceso de suma. Estos se muestran en la siguiente regla, para sumas y potencias de enteros, y los usamos en el siguiente conjunto de ejemplos.

Regla: Sumas y Poderes de Enteros

1. La suma de$n$ números enteros viene dada por

\[\sum_{i=1}^n i=1+2+⋯+n=\dfrac{n(n+1)}{2}. \label{sum1} \]

2. La suma de números enteros consecutivos al cuadrado viene dada por

\[\sum_{i=1}^n i^2=1^2+2^2+⋯+n^2=\dfrac{n(n+1)(2n+1)}{6}. \label{sum2} \]

3. La suma de números enteros consecutivos en cubos viene dada por

\[\sum_{i=1}^n i^3=1^3+2^3+⋯+n^3=\dfrac{n^2(n+1)^2}{4}. \label{sum3} \]

Ejemplo$\PageIndex{2}$: Evaluation Using Sigma Notation

Escribe usando notación sigma y evalúa:

La suma de los términos$(i−3)^2$ para$i=1,2,…,200.$
La suma de los términos$(i^3−i^2)$ para$i=1,2,3,4,5,6$

Solución

a. Multiplicando$(i−3)^2$, podemos romper la expresión en tres términos.

\ [\ begin {alinear*}\ suma_ {i=1} ^ {200} (i−3) ^2 &=\ suma_ {i=1} ^ {200} (i^2−6i+9)\\ [4pt]
&=\ suma_ {i=1} ^ {200} i^2−\ suma_ {i=1} ^ {200} 6i+\ sum_ {i=1} ^ ^ {200} 9\\ [4pt]
&=\ suma_ {i=1} ^ {200} i^2−6\ suma_ {i=1} ^ {200} i+\ suma_ {i=1} ^ {200} 9\\ [4pt]
&=\ dfrac {200 (200+1) (400+1)} {6} −6\ izquierda [\ dfrac {200 (200+1)} {2}\ derecha] +9 (200)\\ [4pt]
&=2.686.700−120,600+1800\\ [4pt]
&=2.567.900\ end {align*}\]

b. Utilizar la propiedad de notación sigma iv. y las reglas para la suma de términos cuadrados y la suma de términos en cubos.

\ [\ begin {alinear*}\ sum_ {i=1} ^ {6} (i^3−i^2) &=\ suma_ {i=1} ^6 i^3−\ suma_ {i=1} ^6 i^2\\ [4pt]
&=\ dfrac {6^2 (6+1) ^2} {4} −\ dfrac {6 (6+1) (2 (6) +1)} {6}\\ [4pt]
&=\ dfrac {1764} {4} −\ dfrac {546} {6}\\ [4pt]
&=350\ end {align*}\ nonumber\]

Ejercicio$\PageIndex{2}$

Encuentra la suma de los valores de$4+3i$ for$i=1,2,…,100.$

Pista: Utilice las propiedades de la notación sigma para resolver el problema.

Contestar: $15,550$

Ejemplo$\PageIndex{3}$: Finding the Sum of the Function Values

Encuentra la suma de los valores de$f(x)=x^3$ sobre los enteros$1,2,3,…,10.$

Solución

Usando la ecuación\ ref {sum3}, tenemos

\[\sum_{i=0}^{10}i^3=\dfrac{(10)^2(10+1)^2}{4}=\dfrac{100(121)}{4}=3025 \nonumber \]

Ejercicio$\PageIndex{3}$

Evaluar la suma que indica la notación$\displaystyle \sum_{k=1}^{20}(2k+1)$.

Pista: Usa la regla sobre suma y potencias de enteros (Ecuaciones\ ref {sum1} -\ ref {sum3}).

Contestar: $440$

Aproximación al área

Ahora que tenemos la notación necesaria, volvemos al problema que nos ocupa: aproximar el área bajo una curva. Dejar$f(x)$ ser una función continua, no negativa definida en el intervalo cerrado$[a,b]$. Queremos aproximar el área$A$ delimitada por$f(x)$ arriba, el$x$ eje -abajo, la línea$x=a$ de la izquierda y la línea de$x=b$ la derecha (Figura$\PageIndex{1}$).

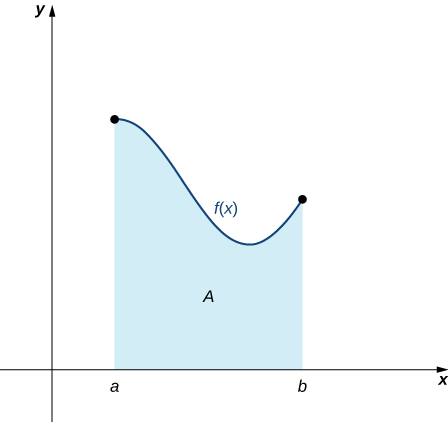
Una gráfica en el cuadrante uno de un área delimitada por una curva genérica f (x) en la parte superior, el eje x en la parte inferior, la línea x = a la izquierda y la línea x = b a la derecha. Aproximadamente a mitad de camino, la concavidad cambia de cóncava hacia abajo a cóncava hacia arriba, y la función comienza a aumentar poco antes de la línea x = b. — Figura$\PageIndex{1}$: Un área (región sombreada) delimitada por la curva$f(x)$ en la parte superior, el$x$ eje -en la parte inferior, la línea$x=a$ a la izquierda y la línea$x=b$ a la derecha.

¿Cómo aproximamos el área bajo esta curva? El enfoque es geométrico. Al dividir una región en muchas formas pequeñas que tienen fórmulas de área conocidas, podemos sumar estas áreas y obtener una estimación razonable del área verdadera. Comenzamos dividiendo el intervalo$[a,b]$ en$n$ subintervalos de igual ancho,$\dfrac{b−a}{n}$. Hacemos esto seleccionando puntos igualmente espaciados$x_0,x_1,x_2,…,x_n$ con$x_0=a,x_n=b,$ y

\[x_i−x_{i−1}=\dfrac{b−a}{n} \nonumber \]

para$i=1,2,3,…,n.$

Denotamos el ancho de cada subintervalo con la notación$Δx,$ so$Δx=\frac{b−a}{n}$ y

\[x_i=x_0+iΔx \nonumber \]

for$i=1,2,3,…,n.$ Esta noción de dividir un intervalo$[a,b]$ en subintervalos seleccionando puntos desde dentro del intervalo se usa con bastante frecuencia para aproximar el área bajo una curva, así que definamos alguna terminología relevante.

Definición: Particiones

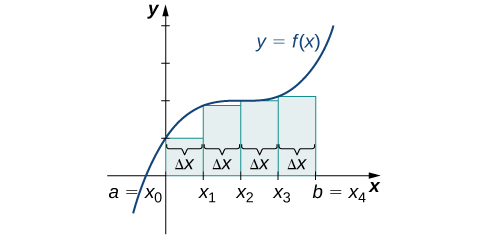
Un conjunto de puntos$P={x_i}$ para$i=0,1,2,…,n$ con$a=x_0 < x_1 < x_2 < ... < x_n = b$, que divide el intervalo$[a, b]$ en subintervalos de la forma$[x_0, x_1], [x_1, x_2], ..., [x_{n-1}, x_n]$ se llama apartición de$[a,b]$. Si todos los subintervalos tienen el mismo ancho, el conjunto de puntos forma una partición regular (o partición uniforme) del intervalo$[a,b].$

Podemos usar esta partición regular como base de un método para estimar el área bajo la curva. A continuación examinamos dos métodos: la aproximación del extremo izquierdo y la aproximación del punto final derecho.

Regla: Aproximación de Extremo Izquierdo

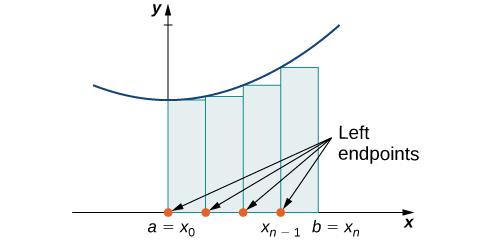
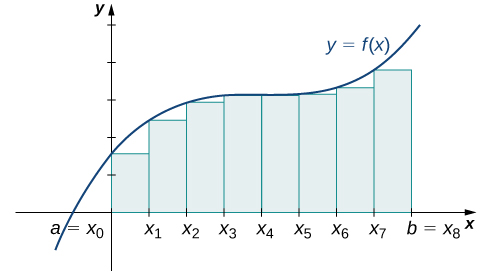
En cada subintervalo$[x_{i−1},x_i]$ (for$i=1,2,3,…,n$), construya un rectángulo con anchura$Δx$ y altura iguales a$f(x_{i−1})$, que es el valor de la función en el punto final izquierdo del subintervalo. Entonces el área de este rectángulo es$f(x_{i−1})Δx$. Sumando las áreas de todos estos rectángulos, obtenemos un valor aproximado para$A$ (Figura$\PageIndex{2}$). Usamos la notación$L_n$ para denotar que esta es una aproximación de extremo izquierdo del$A$ uso de$n$ subintervalos.

\[A≈L_n=f(x_0)Δx+f(x_1)Δx+⋯+f(x_{n−1})Δx=\sum_{i=1}^nf(x_{i−1})Δx \nonumber \]

Diagrama que muestra la aproximación del punto final izquierdo del área bajo una curva. Bajo una parábola con vértice en el eje y y por encima del eje x, se dibujan rectángulos entre a=x0 en el origen y b = xn. Los rectángulos tienen extremos en a=x0, x1, x2... x (n-1), y b = xn, espaciados por igual. La altura de cada rectángulo está determinada por el valor de la función dada en el punto final izquierdo del rectángulo. — Figura$\PageIndex{2}$: En la aproximación del punto final izquierdo del área bajo una curva, la altura de cada rectángulo está determinada por el valor de la función a la izquierda de cada subintervalo.

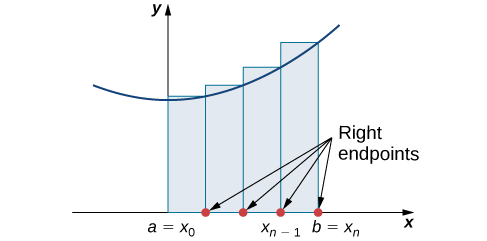
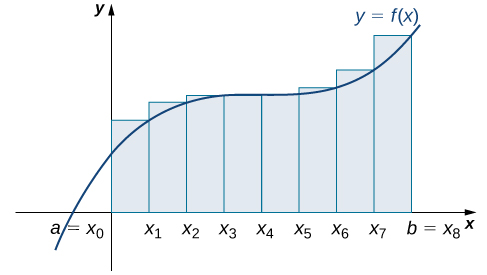
El segundo método para aproximar el área bajo una curva es la aproximación del punto final derecho. Es casi lo mismo que la aproximación del extremo izquierdo, pero ahora las alturas de los rectángulos están determinadas por los valores de función a la derecha de cada subintervalo.

Regla: Aproximación de punto final derecho

Construye un rectángulo en cada subintervalo$[x_{i−1},x_i]$, solo que esta vez la altura del rectángulo está determinada por el valor de la función$f(x_i)$ en el punto final derecho del subintervalo. Entonces, el área de cada rectángulo es$f(x_i)\,Δx$ y la aproximación para$A$ viene dada por

\[A≈R_n=f(x_1)Δx+f(x_2)Δx+⋯+f(x_n)Δx=\sum_{i=1}^nf(x_i)Δx. \nonumber \]

La notación$R_n$ indica que se trata de una aproximación de extremo derecho para$A$ (Figura$\PageIndex{3}$).

Diagrama que muestra la aproximación del punto final derecho del área bajo una curva. Bajo una parábola con vértice en el eje y y por encima del eje x, se dibujan rectángulos entre a=x0 en el origen y b = xn. Los rectángulos tienen extremos en a=x0, x1, x2... x (n-1), y b = xn, espaciados por igual. La altura de cada rectángulo está determinada por el valor de la función dada en el punto final derecho del rectángulo. — Figura$\PageIndex{3}$: En la aproximación del punto final derecho del área bajo una curva, la altura de cada rectángulo está determinada por el valor de la función a la derecha de cada subintervalo. Tenga en cuenta que la aproximación del punto final derecho difiere de la aproximación del extremo izquierdo en la Figura$\PageIndex{2}$.

Las gráficas de la Figura$\PageIndex{4}$ representan la curva$f(x)=\dfrac{x^2}{2}$. En la Figura$\PageIndex{4b}$ dividimos la región representada por el intervalo$[0,3]$ en seis subintervalos, cada uno de ancho$0.5$. Así,$Δx=0.5$. Luego formamos seis rectángulos dibujando líneas verticales perpendiculares a$x_{i−1}$, el punto final izquierdo de cada subintervalo. Determinamos la altura de cada rectángulo calculando$f(x_{i−1})$ para$i=1,2,3,4,5,6.$ Los intervalos son$[0,0.5],[0.5,1],[1,1.5],[1.5,2],[2,2.5],[2.5,3]$. Encontramos el área de cada rectángulo multiplicando la altura por la anchura. Entonces, la suma de las áreas rectangulares se aproxima al área entre$f(x)$ y el$x$ eje. Cuando se utilizan los extremos izquierdos para calcular la altura, tenemos una aproximación de punto final izquierdo. Por lo tanto,

\ [\ begin {alinear*} A≈L_6 &=\ suma_ {i=1} ^6f (x_ {i−1}) Δx =f (x_0) δx+F (x_1) δx+F (x_2) δx+F (x_3) δx+F (x_4) Δx+F (x_5) Δx\ [4pt]
&=f (0) 0.5+f (0.5) 0.5+f (1) 0.5+f (1.5) 0.5+f (2) 0.5+f (2.5) 0.5\\ [4pt]
& =( 0) 0.5+ (0.125) 0.5+ (0.5) 0.5+ (1.125) 0.5+ (2) 0.5+ (3.125) 0.5\\ [4pt]
&=0+0.0625 +0.25+0.5625+1+1.5625\\ [4pt]
&=3.4375\,\ texto {unidades} ^2\ end {align*}\ nonumber\]

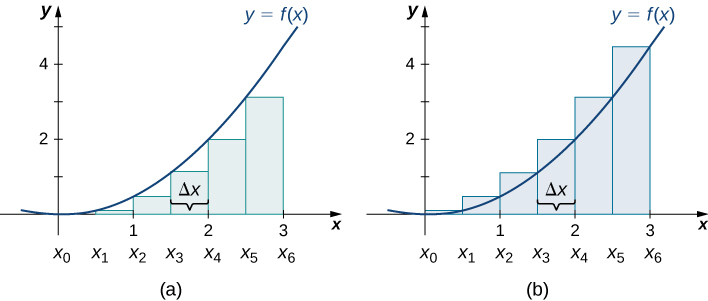
Diagramas lado a lado, mostrando las diferencias en la aproximación del área bajo una curva parabólica con vértice en el origen entre el método de puntos finales izquierdos (el primer diagrama) y el método de extremos derechos (el segundo diagrama). En el primer diagrama, los rectángulos se dibujan a intervalos pares (delta x) bajo la curva con alturas determinadas por el valor de la función en los extremos izquierdos. En el segundo diagrama, los rectángulos se dibujan de la misma manera, pero con alturas determinadas por el valor de la función en los extremos derechos. Los puntos finales en ambos están espaciados por igual desde el origen a (3, 0), etiquetados x0 a x6. — Figura$\PageIndex{4}$: Métodos de aproximación del área bajo una curva usando (a) los extremos izquierdos y (b) los extremos derechos.

En la Figura$\PageIndex{4b}$, dibujamos líneas verticales perpendiculares a$x_i$ tal que$x_i$ sea el punto final correcto de cada subintervalo, y calculamos$f(x_i)$ para$i=1,2,3,4,5,6$. Multiplicamos cada uno$f(x_i)$ por$Δx$ para encontrar las áreas rectangulares, y luego agregarlas. Esta es una aproximación del punto final derecho del área debajo$f(x)$. Por lo tanto,

\ [\ begin {alinear*} A≈R_6 &=\ suma_ {i=1} ^6f (x_i) δx=F (x_1) δx+F (x_2) δx+F (x_3) δx+F (x_4) δx+F (x_5) δx+F (x_6) Δx\\ [4pt]
&=f (0.5) 0.5+f (1) 0.5+f (1.5) 0.5+f (2) 0.5+f (2.5) 0.5+f (3) 0.5\\ [4pt]
& =( 0.125) 0.5+ (0.5) 0.5+ (1.125) 0.5+ (2) 0.5+ (3.125) 0.5+ (4.5) 0.5\\ [4pt]
&=0.0625+0.25 +0.5625+1+1.5625+2.25\\ [4pt]
&=5.6875\,\ texto {unidades} ^2. \ end {align*}\ nonumber\]

Ejemplo$\PageIndex{4}$: Approximating the Area Under a Curve

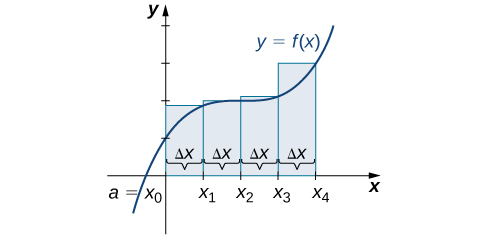
Utilice ambas aproximaciones de extremo izquierdo y extremo derecho para aproximar el área bajo la curva de$f(x)=x^2$ en el intervalo$[0,2]$; use$n=4$.

Solución

Primero, divida el intervalo$[0,2]$ en subintervalos$n$ iguales. Usando$n=4,\, Δx=\dfrac{(2−0)}{4}=0.5$. Este es el ancho de cada rectángulo. Los intervalos$[0,0.5],[0.5,1],[1,1.5],[1.5,2]$ se muestran en la Figura$\PageIndex{5}$. Usando una aproximación de punto final izquierdo, las alturas son$f(0)=0,\,f(0.5)=0.25,\,f(1)=1,$ y$f(1.5)=2.25.$ Entonces,

\[ \begin{align*} L_4 &=f(x_0)Δx+f(x_1)Δx+f(x_2)Δx+f(x_3)Δx \\[4pt] &=0(0.5)+0.25(0.5)+1(0.5)+2.25(0.5) \\[4pt] &=1.75 \,\text{units}^2 \end{align*} \nonumber \]

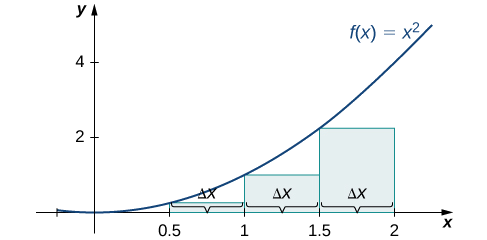
Una gráfica de la aproximación del punto final izquierdo del área bajo la curva f (x) = x^2 de 0 a 2 con puntos finales espaciados .5 unidades. Las alturas del rectángulo están determinadas por los valores de la función en sus extremos izquierdos. — Figura$\PageIndex{5}$: La gráfica muestra la aproximación del punto final izquierdo del área bajo$f(x)=x^2$ de$0$ a$2$.

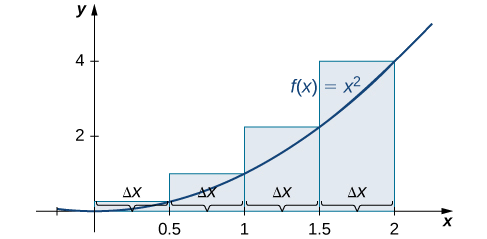
La aproximación del punto final derecho se muestra en la Figura$\PageIndex{6}$. Los intervalos son los mismos,$Δx=0.5,$ pero ahora usa el punto final correcto para calcular la altura de los rectángulos. Tenemos

\[ \begin{align*} R_4 &=f(x_1)Δx+f(x_2)Δx+f(x_3)Δx+f(x_4)Δx \\[4pt] &=0.25(0.5)+1(0.5)+2.25(0.5)+4(0.5) \\[4pt] &=3.75 \,\text{units}^2 \end{align*} \nonumber \]

Un gráfico del método de aproximación del punto final derecho del área bajo la curva f (x) = x^2 de 0 a 2 con puntos finales espaciados .5 unidades. Las alturas de los rectángulos están determinadas por los valores de la función en los extremos correctos. — Figura$\PageIndex{6}$: La gráfica muestra la aproximación del punto final derecho del área bajo$f(x)=x^2$ de$0$ a$2$.

La aproximación del punto final izquierdo es$1.75\,\text{units}^2$; la aproximación del punto final derecho es$3.75 \,\text{units}^2$.

Ejercicio$\PageIndex{4}$

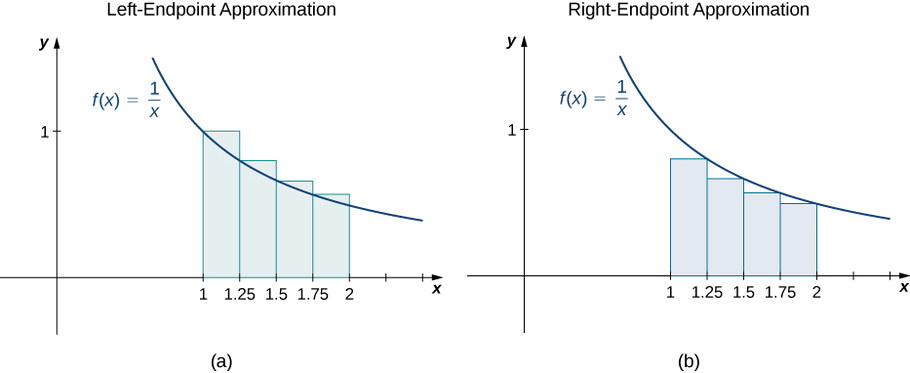
Croquis aproximaciones de punto final izquierdo y extremo derecho para$f(x)=\dfrac{1}{x}$ on$[1,2]$; use$n=4$. Aproximar el área usando ambos métodos.

Pista: Siga la estrategia de resolución en Ejemplo$\PageIndex{4}$ paso a paso.

Contestar

La aproximación del extremo izquierdo es$0.7595 \,\text{units}^2$. La aproximación del punto final derecho es$0.6345 \,\text{units}^2$. Ver los siguientes Medios de comunicación.

$Dos gráficas lado a lado que muestran la aproximación del punto final izquierdo y la aproximación del punto final derecho del área bajo la curva f (x) = 1/x de 1 a 2 con puntos finales espaciados uniformemente en .25 unidades. Las alturas de la aproximación de punto final izquierdo uno están determinadas por los valores de la función en los extremos izquierdos, y la altura de la aproximación de extremo derecho uno se determina por los valores de la función en los extremos derechos.$

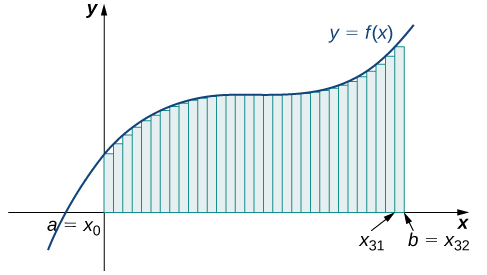
Mirando Figura$\PageIndex{4}$ y las gráficas en Ejemplo$\PageIndex{4}$, podemos ver que cuando usamos un pequeño número de intervalos, ni la aproximación del extremo izquierdo ni la aproximación del punto final derecho son una estimación particularmente precisa del área bajo la curva. No obstante, parece lógico que si aumentamos el número de puntos en nuestra partición, nuestra estimación de$A$ mejorará. Tendremos más rectángulos, pero cada rectángulo será más delgado, así podremos ajustar los rectángulos a la curva con mayor precisión.

Podemos demostrar la aproximación mejorada obtenida a través de intervalos más pequeños con un ejemplo. Exploremos la idea de aumentar$n$, primero en una aproximación de extremo izquierdo con cuatro rectángulos, luego ocho rectángulos, y finalmente$32$ rectángulos. Entonces, hagamos lo mismo en una aproximación de punto final derecho, usando los mismos conjuntos de intervalos, de la misma región curva. La figura$\PageIndex{7}$ muestra el área de la región bajo la curva$f(x)=(x−1)^3+4$ en el intervalo$[0,2]$ usando una aproximación de punto final izquierdo donde$n=4.$ El ancho de cada rectángulo es

\[Δx=\dfrac{2−0}{4}=\dfrac{1}{2}.\nonumber \]

El área se aproxima por las áreas sumadas de los rectángulos, o

\[L_4=f(0)(0.5)+f(0.5)(0.5)+f(1)(0.5)+f(1.5)0.5=7.5 \,\text{units}^2\nonumber \]

Una gráfica de la aproximación del punto final izquierdo del área bajo la curva dada de a = x0 a b=x4. Las alturas de los rectángulos están determinadas por los valores de la función en los extremos izquierdos. — Figura$\PageIndex{7}$: Con una aproximación de extremo izquierdo y dividiendo la región de$a$ a$b$ en cuatro intervalos iguales, el área bajo la curva es aproximadamente igual a la suma de las áreas de los rectángulos.

La figura$\PageIndex{8}$ muestra la misma curva dividida en ocho subintervalos. Comparando la gráfica con cuatro rectángulos en la Figura$\PageIndex{7}$ con esta gráfica con ocho rectángulos, podemos ver que parece haber menos espacio en blanco bajo la curva cuando$n=8.$ Este espacio en blanco es área bajo la curva que no podemos incluir usando nuestra aproximación. El área de los rectángulos es

\[L_8=f(0)(0.25)+f(0.25)(0.25)+f(0.5)(0.25)+f(0.75)(0.25)+f(1)(0.25)+f(1.25)(0.25)+f(1.5)(0.25)+f(1.75)(0.25)=7.75 \,\text{units}^2\nonumber \]

Un gráfico que muestra la aproximación del punto final izquierdo para el área bajo la curva dada de a=x0 a b = x8. Las alturas de los rectángulos están determinadas por los valores de la función en los extremos izquierdos. — Figura$\PageIndex{8}$: La región bajo la curva se divide en áreas$n=8$ rectangulares de igual ancho para una aproximación de extremo izquierdo.

La gráfica de la Figura$\PageIndex{9}$ muestra la misma función con$32$ rectángulos inscritos bajo la curva. Parece que queda poco espacio en blanco. El área ocupada por los rectángulos es

\[L_{32}=f(0)(0.0625)+f(0.0625)(0.0625)+f(0.125)(0.0625)+⋯+f(1.9375)(0.0625)=7.9375 \,\text{units}^2.\nonumber \]

Una gráfica de la aproximación del punto final izquierdo del área bajo la curva dada de a = x0 a b = x32. Las alturas de los rectángulos están determinadas por los valores de la función en los extremos izquierdos. — Figura$\PageIndex{9}$: Aquí,$32$ los rectángulos se inscriben bajo la curva para una aproximación de extremo izquierdo.

Podemos llevar a cabo un proceso similar para el método de aproximación del punto final derecho. Una aproximación del punto final derecho de la misma curva, usando cuatro rectángulos (Figura$\PageIndex{10}$), produce un área

\[R_4=f(0.5)(0.5)+f(1)(0.5)+f(1.5)(0.5)+f(2)(0.5)=8.5 \,\text{units}^2.\nonumber \]

Una gráfica de la aproximación del punto final derecho para el área bajo la curva dada de x0 a x4. Las alturas de los rectángulos están determinadas por los valores de la función en los extremos correctos. — Figura$\PageIndex{10}$: Ahora dividimos el área bajo la curva en cuatro subintervalos iguales para una aproximación de punto final derecho.

Dividir la región sobre el intervalo$[0,2]$ en ocho rectángulos da como resultado$Δx=\dfrac{2−0}{8}=0.25.$ La gráfica se muestra en la Figura$\PageIndex{11}$. El área es

\[R_8=f(0.25)(0.25)+f(0.5)(0.25)+f(0.75)(0.25)+f(1)(0.25)+f(1.25)(0.25)+f(1.5)(0.25)+f(1.75)(0.25)+f(2)(0.25)=8.25 \,\text{units}^2\nonumber \]

Una gráfica de la aproximación del punto final derecho para el área bajo la curva dada de a=x0 a B=X8.Las alturas de los rectángulos están determinadas por los valores de la función en los extremos de la derecha. — Figura$\PageIndex{11}$: Aquí se utiliza la aproximación de punto final derecho para una región dividida en ocho subintervalos iguales.

Por último, la aproximación del punto final derecho con$n=32$ está cerca del área real (Figura$\PageIndex{12}$). El área es aproximadamente

\[R_{32}=f(0.0625)(0.0625)+f(0.125)(0.0625)+f(0.1875)(0.0625)+⋯+f(2)(0.0625)=8.0625 \,\text{units}^2\nonumber \]

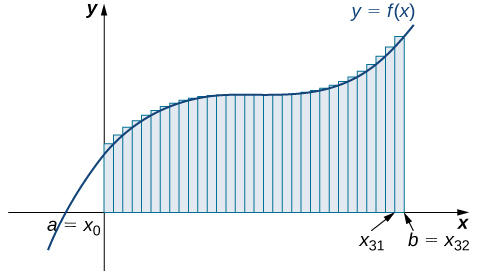
Una gráfica de la aproximación del punto final derecho para el área bajo la curva dada de a=x0 a b=x32. Las alturas de los rectángulos están determinadas por los valores de la función en los extremos correctos. — Figura$\PageIndex{12}$: La región se divide en subintervalos$32$ iguales para una aproximación de punto final derecho.

Con base en estas cifras y cálculos, parece que estamos en el camino correcto; los rectángulos aparecen para aproximar mejor el área bajo la curva a medida que$n$ se hace más grande. Además, a$n$ medida que aumenta, las aproximaciones de extremo izquierdo y extremo derecho parecen acercarse a un área de unidades$8$ cuadradas. $\PageIndex{15}$La tabla muestra una comparación numérica de los métodos de punto final izquierdo y derecho. La idea de que las aproximaciones del área bajo la curva se hacen cada vez mejores a medida que$n$ se hace cada vez más grande es muy importante, y ahora exploramos esta idea con más detalle.

Tabla$\PageIndex{15}$: Valores convergentes de aproximaciones de punto final izquierdo y derecho a medida que$n$ aumenta
Valor de$n$	Área aproximada$L_n$	Área aproximada$R_n$
\ (n\)” style="vertical-align:middle; ">$n=4$	\ (L_n\)” style="vertical-align:middle; ">$7.5$	\ (R_n\)” style="vertical-align:middle; ">$8.5$
\ (n\)” style="vertical-align:middle; ">$n=8$	\ (L_n\)” style="vertical-align:middle; ">$7.75$	\ (R_n\)” style="vertical-align:middle; ">$8.25$
\ (n\)” style="vertical-align:middle; ">$n=32$	\ (L_n\)” style="vertical-align:middle; ">$7.94$	\ (R_n\)” style="vertical-align:middle; ">$8.06$

Formando sumas de Riemann

Hasta el momento hemos estado usando rectángulos para aproximar el área bajo una curva. Las alturas de estos rectángulos se han determinado evaluando la función en los extremos derecho o izquierdo del subintervalo$[x_{i−1},x_i]$. En realidad, no hay razón para restringir la evaluación de la función a uno de estos dos puntos solamente. Podríamos evaluar la función en cualquier punto$x^∗_i$ del subintervalo$[x_{i−1},x_i]$, y usarla$f(x^∗_i)$ como la altura de nuestro rectángulo. Esto nos da una estimación para el área del formulario

\[A≈\sum_{i=1}^nf(x^∗_i)\,Δx. \nonumber \]

Una suma de esta forma se llama suma de Riemann, llamada así por el matemático del siglo XIX Bernhard Riemann, quien desarrolló la idea.

Definición: Riemann sum

Dejar$f(x)$ ser definido en un intervalo cerrado$[a,b]$ y dejar$P$ ser cualquier partición de$[a,b]$. Dejar$Δx_i$ ser el ancho de cada subintervalo$[x_{i−1},x_i]$ y para cada uno$i$, dejar$x^∗_i$ ser cualquier punto adentro$[x_{i−1},\,x_i]$. Una suma de Riemann se define$f(x)$ como

\[\sum_{i=1}^nf(x^∗_i)\,Δx_i. \nonumber \]

En este punto, elegiremos una partición regular$P$, como tenemos en nuestros ejemplos anteriores. Esto obliga$Δx_i$ a todos a ser iguales a$Δx = \dfrac{b-a}{n}$ para cualquier número natural de intervalos$n$.

Recordemos que con las aproximaciones de punto final izquierdo y derecho, las estimaciones parecen mejorar y mejorar a medida que se$n$ hacen cada vez más grandes. Lo mismo sucede con las sumas de Riemann. Las sumas de Riemann dan mejores aproximaciones para valores mayores de$n$. Ahora estamos listos para definir el área bajo una curva en términos de sumas de Riemann.

Definición: Área bajo la curva

Dejar$f(x)$ ser una función continua, no negativa en un intervalo$[a,b]$, y dejar$\displaystyle \sum_{i=1}^nf(x^∗_i)\,Δx$ ser una suma de Riemann para$f(x)$ con una partición regular$P$. Luego, el área bajo$y=f(x)$ la curva$[a,b]$ está dada por

\[A=\lim_{n→∞}\sum_{i=1}^nf(x^∗_i)\,Δx. \nonumber \]

Vea una demostración gráfica de la construcción de una suma Riemann.

Aquí vale la pena discutir algunas sutilezas. Primero, tenga en cuenta que tomar el límite de una suma es un poco diferente de tomar el límite de una función$f(x)$ como$x$ va al infinito. Los límites de las sumas se discuten en detalle en el capítulo de Secuencias y Series; sin embargo, por ahora podemos suponer que las técnicas computacionales que utilizamos para calcular límites de funciones también pueden ser utilizadas para calcular límites de sumas.

Segundo, debemos considerar qué hacer si la expresión converge a diferentes límites para diferentes elecciones de${x^∗_i}.$ Afortunadamente, esto no sucede. Si bien la prueba está más allá del alcance de este texto, se puede demostrar que si$f(x)$ es continua en el intervalo cerrado$[a,b]$, entonces$\displaystyle \lim_{n→∞}\sum_{i=1}^nf(x^∗_i)Δx$ existe y es única (es decir, no depende de la elección de${x^∗_i}$).

Nos fijamos en algunos ejemplos en breve. Pero, antes de hacerlo, tomemos un momento y hablemos de algunas opciones específicas para${x^∗_i}$. Aunque cualquier opción para nos${x^∗_i}$ da una estimación del área bajo la curva, no necesariamente sabemos si esa estimación es demasiado alta (sobreestimar) o demasiado baja (subestimar). Si es importante saber si nuestra estimación es alta o baja, podemos seleccionar nuestro valor${x^∗_i}$ para garantizar un resultado u otro.

Si queremos una sobreestimación, por ejemplo, podemos elegir${x^∗_i}$ tal que$i=1,2,3,…,n,$$f(x^∗_i)≥f(x)$ para todos$x∈[x_i−1,x_i]$. En otras palabras, elegimos para${x^∗_i}$ que for$i=1,2,3,…,n,$$f(x^∗_i)$ sea el valor máximo de la función en el intervalo$[x_{i−1},x_i]$. Si seleccionamos de esta${x^∗_i}$ manera, entonces la suma de Riemann$\displaystyle \sum_{i=1}^nf(x^∗_i)Δx$ se llama suma superior. Del mismo modo, si queremos una subestimación, podemos elegir para${x∗i}$ que for$i=1,2,3,…,n,$$f(x^∗_i)$ sea el valor mínimo de la función en el intervalo$[x_{i−1},x_i]$. En este caso, la suma asociada de Riemann se denomina suma menor. Tenga en cuenta que si$f(x)$ está aumentando o disminuyendo a lo largo del intervalo$[a,b]$, entonces los valores máximo y mínimo de la función ocurren en los puntos finales de los subintervalos, por lo que las sumas superior e inferior son exactamente las mismas que las aproximaciones de punto final izquierdo y derecho.

Ejemplo$\PageIndex{5}$: Finding Lower and Upper Sums

Encuentra una suma menor para$f(x)=10−x^2$ on$[1,2]$; let$n=4$ subintervalos.

Solución

Con$n=4$ sobre el intervalo$[1,2], \,Δx=\dfrac{1}{4}$. Podemos enumerar los intervalos como$[1,1.25],\,[1.25,1.5],\,[1.5,1.75],$ y$[1.75,2]$. Debido a que la función está disminuyendo a lo largo del intervalo$[1,2],$ La figura muestra que se obtiene una suma menor mediante el uso de los extremos correctos.

La gráfica de f (x) = 10 − x^2 de 0 a 2. Se configura para una aproximación del extremo derecho del área delimitada por la curva y el eje x en [1, 2], etiquetada a=x0 a x4. Muestra una suma menor. — Figura$\PageIndex{13}$: La gráfica de$f(x)=10−x^2$ se configura para una aproximación del punto final derecho del área delimitada por la curva y el$x$ eje sobre$[1,2]$, y muestra una suma menor.

La suma de Riemann es

\ [\ begin {align*}\ sum_ {k=1} ^4 (10−x^2) (0.25) &=0.25 [10− (1.25) ^2+10− (1.5) ^2+10− (1.75) ^2+10− (2) ^2]\\ [4pt]
&=0.25 [8.4375+7.75+6.9375+6]\\ [4pt] &=7.75+6.9375+6]\\ [4pt]
&=7.75+6.9375+6]\\ [4pt] 28\,\ texto {unidades} ^2. \ end {alinear*}\]

El área de$7.28$$\text{units}^2$ es una suma menor y una subestimación.

Ejercicio$\PageIndex{5}$

Encuentra una suma superior para$f(x)=10−x^2$ on$[1,2]$; let$n=4.$
Esbozar la aproximación.

Pista: $f(x)$está disminuyendo on$[1,2]$, por lo que los valores máximos de la función ocurren en los puntos finales izquierdos de los subintervalos.

Contestar

a. Suma superior=$8.0313 \,\text{units}^2.$

$Una gráfica de la función f (x) = 10 − x^2 de 0 a 2. Se configura para una aproximación de punto final derecho sobre el área [1,2], que se etiqueta a=x0 a x4. Es una suma superior.$

Ejemplo$\PageIndex{6}$: Finding Lower and Upper Sums for $f(x)=\sin x$

Encuentra una suma más baja para$f(x)=\sin x$ sobre el intervalo$[a,b]=\left[0,\frac{π}{2} \right]$; vamos$n=6.$

Solución

Veamos primero la gráfica en Figura$\PageIndex{14}$ para tener una mejor idea del área de interés.

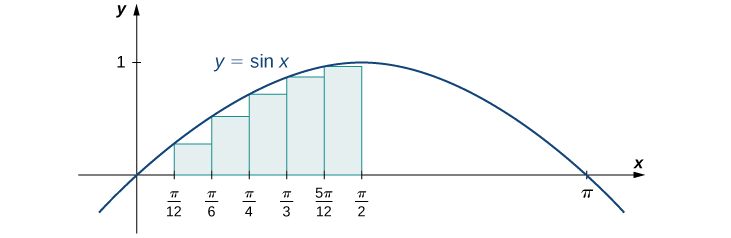
Una gráfica de la función y = sin (x) de 0 a pi. Se configura para una aproximación de punto final izquierdo de 0 a pi/2 y n=6. Es una suma menor. — Figura$\PageIndex{14}$: La gráfica de$y=\sin x$ se divide en seis regiones:$Δx=\dfrac{π/2}{6}=\dfrac{π}{12}$.

Los intervalos son$\left[0,\frac{π}{12}\right],\,\left[\frac{π}{12},\frac{π}{6}\right],\,\left[\frac{π}{6},\frac{π}{4}\right],\,\left[\frac{π}{4},\frac{π}{3}\right],\,\left[\frac{π}{3},\frac{5π}{12}\right]$, y$\left[\frac{5π}{12},\frac{π}{2}\right]$. Obsérvese que$f(x)=\sin x$ va aumentando en el intervalo$\left[0,\frac{π}{2}\right]$, por lo que una aproximación de extremo izquierdo nos da la suma más baja. Una aproximación de extremo izquierdo es la suma de Riemann$\sum_{i=0}^5\sin x_i\left(\tfrac{π}{12}\right)$. Tenemos

\[A≈\sin(0)\left(\tfrac{π}{12}\right)+\sin\left(\tfrac{π}{12}\right)\left(\tfrac{π}{12}\right)+\sin\left(\tfrac{π}{6}\right)\left(\tfrac{π}{12}\right)+\sin\left(\tfrac{π}{4}\right)\left(\tfrac{π}{12}\right)+\sin\left(\tfrac{π}{3}\right)\left(\tfrac{π}{12}\right)+\sin\left(\tfrac{5π}{12}\right)\left(\tfrac{π}{12}\right)\approx 0.863 \,\text{units}^2. \nonumber \]

Ejercicio$\PageIndex{6}$

Usando la función$f(x)=\sin x$ sobre el intervalo$\left[0,\frac{π}{2}\right],$ encontrar una suma superior; vamos$n=6.$

Pista: Siga los pasos de Ejemplo$\PageIndex{6}$.

Contestar: $A≈1.125 \,\text{units}^2$

Conceptos clave

El uso de la notación sigma (suma) de la forma$\displaystyle \sum_{i=1}^na_i$ es útil para expresar sumas largas de valores en forma compacta.
Para una función continua definida sobre un intervalo$[a,b],$ el proceso de dividir el intervalo en partes$n$ iguales, extender un rectángulo a la gráfica de la función, calcular las áreas de la serie de rectángulos, y luego sumar las áreas produce una aproximación del área de esa región.
Cuando se usa una partición regular, el ancho de cada rectángulo es$Δx=\dfrac{b−a}{n}$.
Las sumas de Riemann son expresiones de la forma$\displaystyle \sum_{i=1}^nf(x^∗_i)Δx,$ y se pueden usar para estimar el área bajo la curva Las aproximaciones de punto final$y=f(x).$ izquierdo y derecho son tipos especiales de sumas de Riemann donde los valores de${x^∗_i}$ se eligen para ser los extremos izquierdo o derecho de los subintervalos, respectivamente.
Las sumas de Riemann permiten mucha flexibilidad en la elección del conjunto de puntos${x^∗_i}$ en los que se evalúa la función, a menudo con miras a obtener una suma inferior o una suma superior.

Ecuaciones Clave

Propiedades de Sigma Notation

\ [\ begin {alinear*}\ suma_ {i=1} ^nc&=nc\\ [4pt]
\ suma_ {i=1} ^nca_i &=c\ suma_ {i=1} ^na_i\ [4pt]
\ suma_ {i=1} ^n (a_i+b_i) &=\ suma_ {i=1} ^na_i+\ sum_ {=1} ^nb_i\\ [4pt]
\ suma_ {i=1} ^n (a_i−b_i) &=\ suma_ {i=1} ^na_i−\ suma_ {i=1} ^nb_i\\ [4pt]
\ suma_ {i=1} ^na_i&=\ suma_ {i=1} ^ma_i+\ suma_ {i=m+1} ^na_i\ final {alinear*}\]

Sumas y Poderes de Enteros

\[\sum_{i=1}^ni=1+2+⋯+n=\dfrac{n(n+1)}{2} \nonumber \]

\[\sum_{i=1}^ni^2=1^2+2^2+⋯+n^2=\dfrac{n(n+1)(2n+1)}{6} \nonumber \]

\[\sum_{i=0}^ni^3=1^3+2^3+⋯+n^3=\dfrac{n^2(n+1)^2}{4} \nonumber \]

Aproximación de extremo izquierdo

$A≈L_n=f(x_0)Δx+f(x_1)Δx+⋯+f(x_{n−1})Δx=\displaystyle \sum_{i=1}^nf(x_{i−1})Δx$

Aproximación de punto final derecho

$A≈R_n=f(x_1)Δx+f(x_2)Δx+⋯+f(x_n)Δx=\displaystyle \sum_{i=1}^nf(x_i)Δx$

Glosario

aproximación de extremo izquierdo: una aproximación del área bajo una curva calculada usando el punto final izquierdo de cada subintervalo para calcular la altura de los lados verticales de cada rectángulo

suma inferior: una suma obtenida usando el valor mínimo de$f(x)$ en cada subintervalo

partición: un conjunto de puntos que divide un intervalo en subintervalos

partición regular: una partición en la que todos los subintervalos tienen el mismo ancho

suma riemann: una estimación del área bajo la curva de la forma$A≈\displaystyle \sum_{i=1}^nf(x^∗_i)Δx$

aproximación de punto final derecho: la aproximación del punto final derecho es una aproximación del área de los rectángulos bajo una curva usando el punto final derecho de cada subintervalo para construir los lados verticales de cada rectángulo

notación sigma: (también, notación de suma) la letra griega sigma ($Σ$) indica la suma de los valores; los valores del índice por encima y por debajo de la sigma indican dónde comenzar la suma y dónde terminarla

suma superior: una suma obtenida usando el valor máximo de$f(x)$ en cada subintervalo

Valor de\(n\)	Área aproximada\(L_n\)	Área aproximada\(R_n\)
\ (n\)” style="vertical-align:middle; ">\(n=4\)	\ (L_n\)” style="vertical-align:middle; ">\(7.5\)	\ (R_n\)” style="vertical-align:middle; ">\(8.5\)
\ (n\)” style="vertical-align:middle; ">\(n=8\)	\ (L_n\)” style="vertical-align:middle; ">\(7.75\)	\ (R_n\)” style="vertical-align:middle; ">\(8.25\)
\ (n\)” style="vertical-align:middle; ">\(n=32\)	\ (L_n\)” style="vertical-align:middle; ">\(7.94\)	\ (R_n\)” style="vertical-align:middle; ">\(8.06\)

Search

Ejemplo\(\PageIndex{1}\): Using Sigma Notation

Ejercicio\(\PageIndex{1}\)

Regla: Propiedades de la notación Sigma

Prueba

Regla: Sumas y Poderes de Enteros

Ejemplo\(\PageIndex{2}\): Evaluation Using Sigma Notation

Ejercicio\(\PageIndex{2}\)

Ejemplo\(\PageIndex{3}\): Finding the Sum of the Function Values

Ejercicio\(\PageIndex{3}\)

Definición: Particiones

Regla: Aproximación de Extremo Izquierdo

Regla: Aproximación de punto final derecho

Ejemplo\(\PageIndex{4}\): Approximating the Area Under a Curve

Ejercicio\(\PageIndex{4}\)

Definición: Riemann sum

Definición: Área bajo la curva

Ejemplo\(\PageIndex{5}\): Finding Lower and Upper Sums

Ejercicio\(\PageIndex{5}\)

Ejemplo\(\PageIndex{6}\): Finding Lower and Upper Sums for \(f(x)=\sin x\)

Ejercicio\(\PageIndex{6}\)