11.4: Unidad Tangente y Vectores Normales

Unidad Tangente Vector

Dada una función de valor vectorial suave$\vecs r(t)$, definimos en la Definición 71 que cualquier vector paralelo a$\vecs r^\prime(t_0)$ es tangente a la gráfica de$\vecs r (t)$ at$t=t_0$. A menudo es útil considerar solo la dirección$\vecs r^\prime(t)$ y no su magnitud. Por lo tanto nos interesa el vector unitario en la dirección de$\vecs r^\prime(t)$. Esto lleva a una definición.

Definición$\PageIndex{1}$: Unit Tangent Vector

Dejar$\vecs r (t)$ ser una función suave en un intervalo abierto$I$. El vector tangente unitario$\vecs T(t)$ es

$$\vecs T(t) = \dfrac{1}{\norm{\vecs r^\prime(t)}}\vecs r^\prime(t).$$

Ejemplo$\PageIndex{1}$: Computing the unit tangent vector

Vamos$\vecs r (t) = \langle 3\cos t, 3\sin t, 4t\rangle$. Encuentra$\vecs T(t)$ y computa$\vecs T(0)$ y$\vecs T(1)$.

Solución

Aplicamos Definición$\PageIndex{1}$ para encontrar$\vecs T(t)$.

\ [\ begin {align*}
\ vecs T (t) &=\ dfrac {1} {\ norm {\ vecs r^\ prime (t)}}\ vecs r^\ prime (t)\\ [4pt]
&=\ dfrac {1} {\ sqrt {\ izquierda (-3\ sin t\ derecha) ^2+\ izquierda (3\ cos t\ derecha) ^2+\ izquierda (3\ cos t\ derecha) ^2+ 4^2}}\ langle -3\ sin t,3\ cos t, 4\ rangle\\ [4pt]
&=\ langle -\ dfrac35\ sin t,\ dfrac35\ cos t,\ dfrac 45\ rangle.
\ end {alinear*}\]

Ahora podemos calcular fácilmente$\vecs T(0)$ y$\vecs T(1)$:

$$\begin{align*} \vecs T(0) &= \langle 0,\dfrac35,\dfrac45\rangle\, \\[4pt] \vecs T(1) &= \langle -\dfrac35\sin 1,\dfrac35\cos 1,\dfrac45\rangle \approx \langle -0.505,0.324,0.8\rangle.\end{align*}$$

Estos se trazan en la Figura$\PageIndex{1}$ con sus puntos iniciales en$\vecs r(0)$ y$\vecs r(1)$, respectivamente. (Parecen bastante “cortos” ya que solo son de longitud 1.)

Figura$\PageIndex{1}$: Trazando vectores tangentes unitarios en Ejemplo$\PageIndex{1}$.

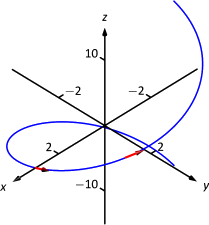
El vector tangente unitario$\vecs T(t)$ siempre tiene una magnitud de 1, aunque a veces es fácil dudar de que sea cierto. Podemos ayudar a solidificar este pensamiento en nuestras mentes computando$\norm{\vecs T(1)}$:

$$\norm{\vecs T(1)} \approx \sqrt{(-0.505)^2+0.324^2+0.8^2} = 1.000001. \nonumber$$

Hemos redondeado en nuestro cómputo de$\vecs T(1)$, así que no obtenemos 1 exactamente. Dejamos al lector usar la representación exacta de$\vecs T(1)$ para verificar que tiene longitud 1.

En muchos sentidos, el ejemplo anterior era “demasiado agradable”. Resultó que siempre$\vecs r^\prime(t)$ fue de longitud 5. En el siguiente ejemplo la longitud de$\vecs r^\prime(t)$ es variable, dejándonos con una fórmula que no es tan limpia.

Ejemplo$\PageIndex{2}$: Computing the unit tangent vector

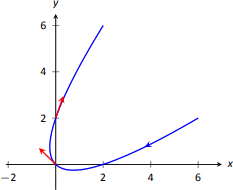
Vamos$\vecs r (t)=\langle t^2-t,t^2+t\rangle$. Encuentra$\vecs T(t)$ y computa$\vecs T(0)$ y$\vecs T(1)$.

Solución

Nos encontramos$\vecs r^\prime(t) = \langle 2t-1,2t+1\rangle$, y

$$\norm{\vecs r^\prime(t)} = \sqrt{(2t-1)^2+(2t+1)^2} = \sqrt{8t^2+2}.$$

Por lo tanto

$$\vecs T(t) = \dfrac{1}{\sqrt{8t^2+2}}\langle 2t-1,2t+1\rangle = \langle \dfrac{2t-1}{\sqrt{8t^2+2}},\dfrac{2t+1}{\sqrt{8t^2+2}}\rangle.$$

Cuando$t=0$, tenemos$\vecs T(0) = \langle -1/\sqrt{2},1/\sqrt{2}\rangle$; cuando$t=1$, tenemos$\vecs T(1) = \langle 1/\sqrt{10}, 3/\sqrt{10}\rangle.$ Dejamos al lector verificar que cada uno de estos es un vector unitario. Se trazan en la Figura$\PageIndex{2}$.

Figura$\PageIndex{2}$: Trazando vectores tangentes unitarios en Ejemplo$\PageIndex{2}$.

Unidad Vector Normal

Así como conocer la dirección tangente a un camino es importante, conocer una dirección ortogonal a un camino es importante. Al tratar con funciones de valor real, definimos la línea normal en un punto al ser la línea a través del punto que era perpendicular a la línea tangente en ese punto. Podemos hacer algo similar con funciones vectoriales. Dado$\vecs r (t)$ en$\mathbb{R}^2$, tenemos 2 direcciones perpendiculares al vector tangente, como se muestra en la Figura$\PageIndex{3}$. Es bueno preguntarse “¿Es preferible una de estas dos direcciones sobre la otra?”

Figura$\PageIndex{3}$: Dada una dirección en el plano, siempre hay dos direcciones ortogonales a éste.

Dado$\vecs r (t)$ en$\mathbb{R}^3$, hay infinitos vectores ortogonales al vector tangente en un punto dado. Nuevamente, podríamos preguntarnos “¿Es preferible una de estas infinitas opciones sobre las demás? ¿Una de estas es la opción “correcta”?

La respuesta en ambos$\mathbb{R}^2$ y$\mathbb{R}^3$ es “Sí, hay un vector que no sólo es preferible, es el “correcto” para elegir”. Recordemos el Teorema 93, que establece que si$\vecs r (t)$ tiene longitud constante, entonces$\vecs r (t)$ es ortogonal a$\vecs r^\prime(t)$ para todos$t$. Sabemos$\vecs T(t)$, el vector tangente unitario, tiene longitud constante. Por lo tanto$\vecs T(t)$ es ortogonal a$\vecs T\,'(t)$.

Veremos que$\vecs T\,'(t)$ es más que una elección conveniente de vector que es ortogonal a$\vecs r^\prime(t)$; más bien, es la elección “correcta”. Como lo único que nos importa es la dirección, definimos este vector recién encontrado como un vector unitario.

Nota:$\vecs T(t)$ es un vector unitario, por definición. Esto no implica que también$\vecs T\,'(t)$ sea un vector unitario.

Definición$\PageIndex{2}$: Unit Normal Vector

Let$\vecs r (t)$ Ser una función de valor vectorial donde el vector tangente unitario,$\vecs T(t)$, es suave en un intervalo abierto$I$. El vector normal unitario$\vecs N(t)$ es

$$\vecs N(t) = \dfrac1{\norm{\vecs T\,'(t)}}\vecs T\,'(t).$$

Ejemplo$\PageIndex{3}$: Computing the unit normal vector

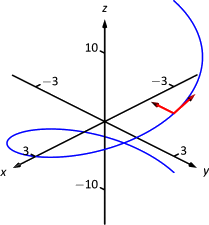
Que$\vecs r (t) = \langle 3\cos t, 3\sin t, 4t\rangle$ como en el Ejemplo 11.4.1. Croquis ambos$\vecs T(\pi/2)$ y$\vecs N(\pi/2)$ con puntos iniciales en$\vecs r(\pi/2)$.

Solución

En Ejemplo$\PageIndex{1}$, encontramos$\vecs T(t) = \langle (-3/5)\sin t,(3/5)\cos t,4/5\rangle$. Por lo tanto

$$\vecs T\,'(t) = \langle -\dfrac35\cos t,-\dfrac35\sin t,0\rangle\quad \text{and} \quad \norm{\vecs T\,'(t)} = \dfrac35.$$

Por lo tanto

$$\vecs N(t) = \dfrac{\vecs T\,'(t)}{3/5} = \langle -\cos t,-\sin t,0\rangle.$$

Calculamos$\vecs T(\pi/2) = \langle -3/5,0,4/5\rangle$ y$\vecs N(\pi/2) = \langle 0,-1,0\rangle$. Estos están bosquejados en la Figura$\PageIndex{4}$.

Figura$\PageIndex{4}$: Trazando vectores tangentes unitarios y normales en Ejemplo$\PageIndex{3}$.

El ejemplo anterior fue una vez más “demasiado agradable”. En general, la expresión for$\vecs T(t)$ contiene fracciones de raíces cuadradas, de ahí que la expresión de$\vecs T\,'(t)$ sea muy desordenada. Esto lo demostramos en el siguiente ejemplo.

Ejemplo$\PageIndex{4}$: Computing the unit normal vector

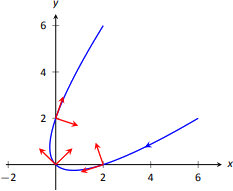
Que$\vecs r (t)=\langle t^2-t,t^2+t\rangle$ como en Ejemplo$\PageIndex{2}$. Buscar$\vecs N(t)$ y bosquejar$\vecs r (t)$ con los vectores tangentes unitarios y normales en$t=-1,0$ y 1.

Solución

En Ejemplo$\PageIndex{2}$, encontramos

$$\vecs T(t) = \langle \dfrac{2t-1}{\sqrt{8t^2+2}},\dfrac{2t+1}{\sqrt{8t^2+2}}\rangle.$$

$\vecs T\,'(t)$El hallazgo requiere dos aplicaciones de la Regla del Cociente:

\ [\ begin {align*}
T' (t) &=\ langle\ dfrac {\ sqrt {8t^2+2} (2) - (2t-1)\ izquierda (\ dfrac12 (8t^2+2) ^ {-1/2} (16t)\ derecha)} {8t^2+2},\\ [4pt]
y quad\\ dfrac {\ sqrt {8t^2+2} (2) - (2t+1)\ izquierda (\ dfrac12 (8t^2+2) ^ {-1/2} (16t)\ derecha)} {8t^2+2}\ rangle\\ [4pt]
&=\ langle\ dfrac {4 (2 t+1)} {\ izquierda (8 t^2+2\ derecha) ^ {3/2}},\ dfrac {4 (1-2 t)} {\ izquierda (8 t^2+2\ derecha) ^ {3/2}}\ rangle
\ end {alinear*}\]

Esto no es un vector unitario; para encontrar$\vecs N(t)$, necesitamos dividir$\vecs T\,'(t)$ por su magnitud.

\ [\ begin {alinear*}
\ norm {\ vecs T\, '(t)} &=\ sqrt {\ dfrac {16 (2t+1) ^2} {(8t^2+2) ^3} +\ dfrac {16 (1-2t) ^2} {(8t^2+2) ^3}}\\ [4pt]
&=\ sqrt {dfrac {16 (8t^2+2)} {(8t^2+2) ^3}}\\ [4pt]
&=\ dfrac {4} {8t^2+2}.
\ end {alinear*}\]

Por último,

\ [\ begin {alinear*}
\ vecs N (t) &=\ dfrac1 {4/ (8t^2+2)}\ langle\ dfrac {4 (2 t+1)} {\ izquierda (8 t^2+2\ derecha) ^ {3/2}},\ dfrac {4
(1-2 t)} {\ izquierda (8 t^2+2\ derecha) ^ {3/2}}\ rangle\\ [4pt]
&=\ langle\ dfrac {2t+1} {\ sqrt {8t^2+2}}, -\ dfrac {2t-1} {\ sqrt {8t^2+2}}\ rangle.
\ end {alinear*}\]

Usando esta fórmula para$\vecs N(t)$, calculamos los vectores tangentes unitarios y normales para$t=-1,0$ y 1 y los bosquejamos en Figura$\PageIndex{5}$.

Figura$\PageIndex{5}$: Trazando vectores tangentes unitarios y normales en Ejemplo$\PageIndex{4}$.

El resultado final para$\vecs N(t)$ en Ejemplo$\PageIndex{4}$ es sospechosamente similar a$\vecs T(t)$. Hay una razón clara para ello. Si$\vecs u = \langle u_1,u_2\rangle$ es un vector unitario en$\mathbb{R}^2$, entonces los únicos vectores unitarios ortogonales a$\vecs u$ son$\langle -u_2,u_1\rangle$ y$\langle u_2,-u_1\rangle$. Dado$\vecs T(t)$, podemos determinar rápidamente$\vecs N(t)$ si sabemos por qué término multiplicar$(-1)$.

Consideremos nuevamente la Figura 11.24, donde hemos trazado algunos vectores tangentes unitarios y normales. Observe cómo$\vecs N(t)$ siempre apunta “dentro” de la curva, o hacia el lado cóncavo de la curva. Esto no es una coincidencia; esto es cierto en general. Conocer la dirección que$\vecs r(t)$ “gira” nos permite encontrar rápidamente$\vecs N(t)$.

TEORAMA$\PageIndex{1}$: Unit Normal Vectors in $\mathbb{R}^2$

Dejar$\vecs r(t)$ ser una función de valor vectorial en$\mathbb{R}^2$ donde$\vecs T\,'(t)$ es suave en un intervalo abierto$I$. $t_0$Déjate entrar$I$ y$\vecs T(t_0) = \langle t_1,t_2\rangle$ Entonces$\vecs N(t_0)$ es o bien

$$\vecs N(t_0) = \langle -t_2,t_1\rangle \quad \text{or}\quad \vecs N(t_0) = \langle t_2,-t_1\rangle,$$

cualquiera que sea el vector que apunta al lado cóncavo de la gráfica de$\vecs r$.

Aplicación a la aceleración

Dejar$\vecs r (t)$ ser una función de posición. Es un hecho (dicho más adelante en Teorema$\PageIndex{2}$) que la aceleración,\ vecs a (t), yace en el plano definido por$\vecs T$ y$\vecs N$. Es decir, hay escalares$a_{\text{T}}$ y$a_{\text{N}}$ tal que

$$\vecs a (t) = a_{\text{T}}\vecs T(t) + a_{\text{N}}\vecs N(t).$$

El escalar$a_{\text{T}}$ mide “cuánta” aceleración hay en la dirección de desplazamiento, es decir, mide el componente de aceleración que afecta la velocidad. El escalar$a_{\text{N}}$ mide “cuánta” aceleración es perpendicular a la dirección de desplazamiento, es decir, mide el componente de aceleración que afecta la dirección de desplazamiento.

Podemos encontrar$a_{\text{T}}$ usando la proyección ortogonal de$\vecs a(t)$ onto$\vecs T(t)$ (revise la Definición 59 en la Sección 10.3 si es necesario).

Recordando que ya que$\vecs T(t)$ es un vector unitario,$\vecs T(t)\cdot\vecs T(t)=1$, por lo que tenemos

$$\text{proj}_{T(t)}\vecs a(t) = \dfrac{\vecs a(t)\cdot\vecs T(t)}{\vecs T(t)\cdot\vecs T(t)}\vecs T(t) = \underbrace{\left(\vecs a(t)\cdot\vecs T(t)\right) }_{a_{\text{T}}}\vecs T(t).$$

Así la cantidad de$\vecs a (t)$ en la dirección de$\vecs T(t)$ es$a_{\text{T}}=\vecs a (t)\cdot\vecs T(t)$. La misma lógica da$a_{\text{N}} = \vecs a (t)\cdot\vecs N(t)$.

Si bien esta es una buena forma de computación$a_{\text{T}}$, hay formas más simples de encontrar$a_{\text{N}}$ (ya que encontrarse a$\vecs N$ sí mismo puede ser complicado). El siguiente teorema da fórmulas alternativas para$a_{\text{T}}$ y$a_{\text{N}}$.

Nota: Tenga en cuenta que ambos$a_\text{T}$ y$a_\text{N}$ son funciones de$t$; es decir, el escalar cambia dependiendo de$t$. Es convención dejar caer la notación$(t)$ ""$a_\text{T}(t)$ y simplemente escribir$a_\text{T}$.

TEORMA$\PageIndex{2}$: Acceleration in the Plane Defined by $\vecs T$ and $\vecs N$

Dejar$\vecs r (t)$ ser una función de posición con aceleración$\vecs a (t)$ y unidad tangente y vectores normales$\vecs T(t)$ y$\vecs N(t)$. Entonces$\vecs a (t)$ yace en el plano definido por$\vecs T(t)$ y$\vecs N(t)$; es decir, existen escalares$a_\text{T}$ y$a_\text{N}$ tal que

$$\vecs a (t) = a_\text{T}\vecs T(t) + a_\text{N}\vecs N(t).$$

Por otra parte,

\ [\ begin {align*}
a_\ text {T} &=\ vecs a (t)\ cdot\ vecs T (t) =\ dfrac {d} {dt}\ left (\ norm {\ vecs v (t)}\ derecha)\\ [4pt]
a_\ text {N} &=\ vecs a (t)\ cdot\ N (t) =\ sqrt {\ norma {\ vecs a (t)} ^2-a_\ texto {T} ^2} =\ dfrac {\ norma {\ vecs a (t)\ veces\ vecs v (t)}} {\ norma {\ vecs v (t)}} =\ norma {\ vecs v (t)}\,\ norma {\ vecs T\, '(t)}
\ final {alinear*}\]

Anote la segunda fórmula para$a_\text{T}$:$\dfrac{d}{dt}\left(\norm{\vecs v (t)}\right)$. Esto mide la tasa de cambio de velocidad, que nuevamente es la cantidad de aceleración en la dirección de desplazamiento.

Ejemplo$\PageIndex{5}$: Computing $a_\text{T}$ and $a_\text{N}$

Dejar$\vecs r (t) = \langle 3\cos t, 3\sin t, 4t\rangle$ como en los Ejemplos 11.4.1 y 11.4.3. Encontrar$a_\text{T}$ y$a_\text{N}$.

Solución

Los ejemplos anteriores dan$\vecs a (t) = \langle -3\cos t,-3\sin t,0\rangle$ y

$$\vecs T(t) = \langle -\dfrac35\sin t,\dfrac35\cos t,\dfrac45\rangle \quad \text{and}\quad \vecs N(t) = \langle -\cos t,-\sin t,0\rangle.$$

Podemos encontrar$a_\text{T}$ y$a_\text{N}$ directamente con productos dot:

\ [\ begin {align*}
a_\ text {T} &=\ vecs a (t)\ cdot\ vecs T (t) =\ dfrac95\ cos t\ sin t-\ dfrac95\ cos t\ sin t+0 = 0.\\ [4pt]
a_\ text {N} &=\ vecs a (t)\ cdot\ vecs N (t) = 3\ cos^2t+3\ sin^2t + 0 = 3.
\ end {alinear*}\]

Así$\vecs a (t) = 0\vecs T(t) + 3\vecs N(t) = 3\vecs N(t)$, que es claramente el caso.

¿Cuál es la interpretación práctica de estos números? $a_\text{T}=0$significa que el objeto se mueve a una velocidad constante y, por lo tanto, toda aceleración viene en forma de cambio de dirección.

Ejemplo$\PageIndex{6}$: Computing $a_\text{T}$ and $a_\text{N}$

Dejar$\vecs r (t)=\langle t^2-t,t^2+t\rangle$ como en Ejemplos$\PageIndex{2}$ y$\PageIndex{4}$. Encontrar$a_\text{T}$ y$a_\text{N}$.

Solución

Los ejemplos anteriores dan$\vecs a(t) = \langle 2,2\rangle$ y

$$\vecs T(t) = \langle \dfrac{2t-1}{\sqrt{8t^2+2}},\dfrac{2t+1}{\sqrt{8t^2+2}}\rangle \nonumber$$

y

$$\vecs N(t) = \langle \dfrac{2t+1}{\sqrt{8t^2+2}},-\dfrac{2t-1}{\sqrt{8t^2+2}}\rangle. \nonumber$$

Si bien podemos calcular$a_\text{N}$ usando$\vecs N(t)$, en su lugar demostramos usando otra fórmula del Teorema$\PageIndex{2}$.

\ [\ begin {alinear*}
a_\ texto {T} &=\ vecs a (t)\ cdot\ vecs T (t) =\ dfrac {4t-2} {\ sqrt {8t^2+2}} +\ dfrac {4t+2} {\ sqrt {8t^2+2}} =\ dfrac {8t} {\ sqrt {8t^2} ^2+2}}.\\ [4pt]
a_\ text {N} &=\ sqrt {\ norm {\ vecs a (t)} ^2-a_\ text {T} ^2} =\ sqrt {8-\ left (\ dfrac {8t} {\ sqrt {8t^2+2}}\ derecha) ^2} =\ dfrac {4} {sqrt {8 t^2+2}}
\ end {alinear*}\]

Cuándo$t=2$,$a_\text{T} = \dfrac{16}{\sqrt{34}}\approx 2.74$ y$a_\text{N} = \dfrac{4}{\sqrt{34}} \approx 0.69$. Interpretamos esto en el sentido de que en$t=2$, la partícula se está acelerando principalmente al aumentar la velocidad, no cambiando de dirección. Como el camino cercano$t=2$ es relativamente recto, esto debería tener sentido intuitivo. La figura$\PageIndex{6}$ da una gráfica de la ruta para referencia.

Figura$\PageIndex{6}$: Graficando$\vecs{r}(t)$ en Ejemplo$\PageIndex{6}$.

Contraste esto con$t=0$, dónde$a_\text{T} = 0$ y$a_\text{N} = 4/\sqrt{2}\approx 2.82$. Aquí la velocidad de la partícula no está cambiando y toda aceleración es en forma de cambio de dirección.

Ejemplo$\PageIndex{7}$: Analyzing projectile motion

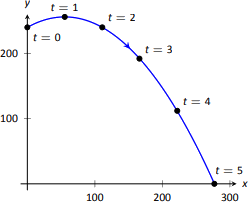
Se lanza una pelota desde una altura de 240ft con una velocidad inicial de 64ft/s y un ángulo de elevación de$30^\circ$. Encuentra la función$\vecs r (t)$ de posición de la pelota y analiza$a_\text{T}$ y$a_\text{N}$.

Solución

Usando la Idea Clave 53 de la Sección 11.3 formamos la función de posición de la pelota:

$$\vecs r (t) = \langle \left(64\cos 30^\circ\right) t, -16t^2+\left(64\sin 30^\circ\right) t+240\rangle,$$

que trazamos en la Figura$\PageIndex{7}$.

Figura$\PageIndex{7}$: Trazando la posición de una pelota lanzada, con incrementos de 1s mostrados.

A partir de esto encontramos$\vecs v (t) = \langle 64\cos 30^\circ, -32t+64\sin 30^\circ\rangle$ y$\vecs a (t) = \langle 0,-32\rangle$. $\vecs T(t)$La computación no es difícil, y con alguna simplificación encontramos

$$\vecs T(t) = \langle \dfrac{\sqrt{3}}{\sqrt{t^2-2t+4}}, \dfrac{1-t}{\sqrt{t^2-2t+4}}\rangle.$$

Con$\vecs a (t)$ lo simple que es, encontrar también$a_\text{T}$ es simple:

$$a_\text{T} = \vecs a (t)\cdot \vecs T(t) = \dfrac{32t-32}{\sqrt{t^2-2t+4}}.$$

Elegimos no encontrar$\vecs N(t)$ y encontrar$a_\text{N}$ a través de la fórmula$a_\text{N} = \sqrt{\norm{\vecs a (t)}^2-a_\text{T}^2\,}$:

$$a_\text{N} = \sqrt{32^2-\left(\dfrac{32t-32}{\sqrt{t^2-2t+4}}\right)^2} = \dfrac{32\sqrt{3}}{\sqrt{t^2-2t+4}}.$$

La figura$\PageIndex{8}$ da una tabla de valores de$a_\text{T}$ y$a_\text{N}$. Cuando$t=0$, vemos que la velocidad de la pelota disminuye; cuando$t=1$ la velocidad de la pelota no cambia. Esto corresponde a que en$t=1$ el balón llega a su punto más alto.

Después$t=1$ vemos que$a_\text{N}$ está disminuyendo en valor. Esto se debe a que a medida que cae la pelota, su camino se vuelve más recto y la mayor parte de la aceleración es en forma de acelerar la pelota, y no en cambiar su dirección.

Figura$\PageIndex{8}$: Una tabla de valores de$a_T$ y$a_N$ en Ejemplo$\PageIndex{7}$.

Nuestra comprensión de los vectores tangentes unitarios y normales nos ayuda a entender el movimiento. El trabajo en Ejemplo$\PageIndex{7}$ dio análisis cuantitativo de lo que intuitivamente sabíamos.

En la siguiente sección se dan dos pasos más importantes hacia este análisis. Actualmente describimos la posición solo en términos de tiempo. En la vida cotidiana, sin embargo, a menudo describimos la posición en términos de distancia (“La gasolinera está a unas 2 millas por delante, a la izquierda”). El parámetro de longitud del arco nos permite referir la posición en términos de distancia recorrida.

También sabemos intuitivamente que algunos caminos son más rectos que otros -y algunos son “más curvos” que otros, pero nos falta una medida de “curva”. El parámetro de longitud del arco nos proporciona una forma de calcular la curvatura, una medida cuantitativa de cuán curvilínea es una curva.