11.5: El parámetro de longitud de arco y curvatura
( \newcommand{\kernel}{\mathrm{null}\,}\)
En conversación normal describimos la posición tanto en términos de tiempo como de distancia. Por ejemplo, imagina conducir para visitar a un amigo. Si ella llama y pregunta dónde estás, podrías responder “Estoy a 20 minutos de tu casa”, o podrías decir “Estoy a 10 millas de tu casa”. Ambas respuestas le dan a tu amigo una idea general de dónde estás.
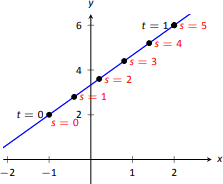
Actualmente, nuestras funciones con valores vectoriales tienen puntos definidos con un parámetrot, que a menudo tomamos para representar el tiempo. Considere Figura11.5.1a, donde⇀r(t)=⟨t2−t,t2+t⟩ se grafica y se muestran los puntos correspondientes at=0, 1 y2 se muestran. Observe cómo la longitud del arco entret=0 yt=1 es menor que la longitud del arco entret=1 yt=2; si el parámetrot es tiempo y⇀r es posición, podemos decir que la partícula viajó más rápido en[1,2] que en[0,1].
Consideremos ahora Figura11.5.1b, donde la misma gráfica es parametrizada por una variable diferentes. Ses=6 trazan los puntos correspondientess=0 a through. La longitud del arco de la gráfica entre cada par de puntos adyacentes es 1. Podemos ver este parámetros como distancia; es decir, la longitud del arco de la gráfica des=0 as=3 es 3, la longitud del arco des=2 as=6 es 4, etc. Si se quiere encontrar el punto 2.5 unidades desde una ubicación inicial (es decir,s=0), se calcularía⇀r(2.5). Este parámetros es muy útil, y se llama el parámetro de longitud de arco.
¿Cómo encontramos el parámetro de longitud de arco?
Comience con cualquier parametrización de⇀r. Podemos calcular la longitud del arco de la gráfica de⇀r en el intervalo[0,t] conarc length =∫t0‖⇀r′(u)‖du. Podemos convertir esto en una función: comot varía, encontramos la longitud del arcos de0 at. Esta función es
s(t)=∫t0‖⇀r′(u)‖du.
Esto establece una relación entres yt. Conociendo esta relación explícitamente, podemos reescribir⇀r(t) en función des:⇀r(s). Esto lo demostramos en un ejemplo.
Ejemplo11.5.1: Finding the arc length parameter
Vamos⇀r(t)=⟨3t−1,4t+2⟩. Parametrizar⇀r con el parámetro de longitud de arcos.}
Solución
Usando la ecuación\ ref {eq:vvfarc}, escribimos
s(t)=∫t0‖⇀r′(u)‖du.
Podemos integrar esto, encontrando explícitamente una relación entres yt:
\ [\ begin {align*}
s (t) &=\ int_0^t\ norm {\ vecs r\, '(u)} du\\ [4pt]
&=\ int_0^t\ sqrt {3^2+4^2} du\\ [4pt]
&=\ int_0^t 5 du\\ [4pt]
&= 5t.
\ end {alinear*}\]
Ya ques=5t, podemos escribirt=s/5 y reemplazart⇀r(t) cons/5:
⇀r(s)=⟨3(s/5)−1,4(s/5)+2⟩=⟨35s−1,45s+2⟩.
Claramente, como se muestra en la Figura11.5.2, la gráfica de⇀r es una línea, dondet=0 corresponde al punto(−1,2). ¿Qué punto de la línea está a 2 unidades de este punto inicial? Lo encontramos cons(2)=⟨1/5,18/5⟩.
¿El punto está(1/5,18/5) realmente a 2 unidades de distancia(−1,2)? Utilizamos la Fórmula de Distancia para verificar:
d=√(15−(−1))2+(185−2)2=√3625+6425=√4=2.
Sí, efectivamentes(2) está a 2 unidades de distancia, en la dirección de desplazamiento, desde el punto inicial.
Las cosas salieron muy bien en Ejemplo11.5.1; pudimos establecer directamente esos=5t. Por lo general, el parámetro de longitud de arco es mucho más difícil de describir en términos det, resultado de integrar una raíz cuadrada. Hay una serie de cosas que podemos aprender sobre el parámetro de longitud de arco de la ecuación\ ref {eq:vvfarc}, sin embargo, que son increíblemente útiles.
Primero, tomar la derivada des con respecto at. El Teorema Fundamental del Cálculo (ver Teorema 39) establece que
dsdt=s′(t)=‖⇀r′(t)‖.
Dejandot representar el tiempo y⇀r(t) representar la posición, vemos que la tasa de cambio des con respecto at es la velocidad; es decir, la tasa de cambio de la “distancia recorrida” es la velocidad, que debe coincidir con nuestra intuición.
La Regla de la Cadena establece que
\ [\ begin {align*}
\ dfrac {d\ vecs r} {dt} &=\ dfrac {d\ vecs r} {ds}\ cdot\ dfrac {ds} {dt}\\ [4pt]
\ vecs r ^\ prime (t) &=\ vecs r ^\ prime (s)\ cdot\ norm {\ vecs r ^ prime (t)}.
\ end {alinear*}\]
Resolviendo para⇀r′(s), tenemos
⇀r′(s)=⇀r′(t)‖⇀r′(t)‖=⇀T(t),
donde⇀T(t) está el vector tangente unitario. La ecuación\ ref {eq:vvfarc2} a menudo se malinterpreta, ya que uno se siente tentado a pensar que afirma⇀r′(t)=⇀T(t), pero hay una gran diferencia entre⇀r′(s) y⇀r′(t). La clave a tomar de él es que⇀r′(s) es un vector unitario. De hecho, el siguiente teorema establece que esto caracteriza al parámetro de longitud de arco.
teorema 99: Parámetro de longitud de arco
Dejar⇀r(s) ser una función vectorizada. El parámetros es el parámetro de longitud de arco si, y solo si,‖⇀r′(s)‖=1.
Curvatura
Considerar puntosA yB en la curva graficada en la Figura11.5.3a. Se puede argumentar fácilmente que la curva se curva más bruscamente enA que enB. Es útil usar un número para describir cuán bruscamente se dobla la curva; ese número es la curvatura de la curva.
Derivamos este número de la siguiente manera. Considere Figura11.5.3b, donde los vectores tangentes unitarios se grafican alrededor de puntosA yB. Observe cómo la dirección del vector tangente unitario cambia bastante cercaA, mientras que no cambia tanto alrededorB. Esto lleva a un concepto importante: medir la tasa de cambio del vector tangente unitario con respecto a la longitud del arco nos da una medida de curvatura.
Definición11.5.1: Curvature
Dejar⇀r(s) ser una función vectorizada dondes está el parámetro de longitud de arco. La curvaturaκ de la gráfica de⇀r(s) es
κ=‖d⇀Tds‖=‖⇀T′(s)‖.
Si⇀r(s) está parametrizado por el parámetro de longitud de arco, entonces
⇀T(s)=⇀r′(s)‖⇀r′(s)‖and⇀N(s)=⇀T′(s)‖⇀T′(s)‖.
Una vez definida‖⇀T′(s)‖=κ, podemos reescribir la segunda ecuación como
⇀T′(s)=κ⇀N(s).
Ya sabíamos que⇀T′(s) está en la misma dirección que⇀N(s); es decir, podemos pensar en ser “tirados” en la dirección de⇀N(s).⇀T(s) ¿Qué tan “duro” está siendo jalado? Por un factor deκ. Cuando la curvatura es grande,⇀T(s) se está “tirando con fuerza” y la dirección de⇀T(s) los cambios rápidamente. Cuandoκ es pequeño, noT(s) se está tirando con fuerza y por lo tanto su dirección no está cambiando rápidamente.
Usamos Definición11.5.1 para encontrar la curvatura de la línea en Ejemplo11.5.2.
Ejemplo11.5.2: Finding the curvature of a line
Use Definición11.5.1 para encontrar la curvatura de⇀r(t)=⟨3t−1,4t+2⟩.
Solución
En Ejemplo\ ref {ex_vvfarc1}, encontramos que el parámetro de longitud de arco estaba definido pors=5t, así⇀r(s)=⟨3t/5−1,4t/5+2⟩ parametrizado⇀r con el parámetro de longitud de arco. Para encontrarκ, tenemos que encontrar⇀T′(s).
⇀T(s)=⇀r′(s)(recall this is a unit vector)=⟨3/5,4/5⟩.
Por lo tanto
⇀T′(s)=⟨0,0⟩
y
κ=‖⇀T′(s)‖=0.
Probablemente no sorprende que la curvatura de una línea sea 0. (¿Qué tan “curvy” es una línea? No tiene curvas en absoluto.)
Si bien la definición de curvatura es un concepto matemático hermoso, es casi imposible de usar la mayor parte del tiempo; escribir⇀r en términos del parámetro de longitud del arco generalmente es muy difícil. Afortunadamente, existen otros métodos para calcular este valor que son mucho más fáciles. Hay una compensación: la definición es “fácil” de entender aunque difícil de calcular, mientras que estas otras fórmulas son fáciles de calcular aunque puede ser difícil entender por qué funcionan.
teorema 100: Fórmulas para la curvatura
DejarC ser una curva suave en un intervalo abiertoI en el plano o en el espacio.
- SiC está definido pory=f(x), entoncesκ=|f′′(x)|(1+(f′(x))2)3/2.
- SiC se define como una función de valor vectorial en el plano,⇀r(t)=⟨x(t),y(t)⟩, entoncesκ=|x′y′′−x′′y′|((x′)2+(y′)2)3/2.
- SiC se define en el espacio por una función de valor vectorial⇀r(t), entoncesκ=‖⇀T′(t)‖‖⇀r′(t)‖=‖⇀r′(t)×⇀r′′(t)‖‖⇀r′(t)‖3=⇀a(t)⋅⇀N(t)‖⇀v(t)‖2.
Practicamos el uso de estas fórmulas.
Ejemplo11.5.3: Finding the curvature of a circle
Encuentra la curvatura de un círculo con radior, definido por⇀c(t)=⟨rcost,rsint⟩.
Solución
Antes de comenzar, debemos esperar que la curvatura de un círculo sea constante, y no dependiente de ellat. (¿Por qué?)
Calculamosκ usando la segunda parte del Teorema 100.
\ [\ begin {align*}
\ kappa &=\ dfrac {| (-r\ sin t) (-r\ sin t) - (-r\ cos t) (r\ cos t) (r\ cos t) |} {\ grande ((-r\ sin t) ^2+ (r\ cos t) ^2\ grande) ^ {3/2}}\\ [4pt]
&=\ dfrac {r^2 (\ sin^2t+\ cos^2t)} {\ grande (r^2 (\ sin^2t+\ cos^2t)\ grande) ^ {3/2}}\\ [4pt]
&=\ dfrac {r^2} {r^3} =\ dfrac1r.
\ end {alinear*}\]
Hemos encontrado que un círculo con radior tiene curvaturaκ=1/r.
11.5.3El ejemplo da un gran resultado. Antes de este ejemplo, si nos dijeran “La curva tiene una curvatura de 5 en el punto”A, no tendríamos idea de lo que esto realmente significaba. Es 5 “grande” - ¿corresponde a un giro realmente brusco, o a un giro no tan agudo? Ahora podemos pensar en 5 en términos de un círculo con radio 1/5. Conocer las unidades (pulgadas vs millas, por ejemplo) nos permite determinar qué tan bruscamente se curva la curva.
Deje queC se dé un puntoP en una curva suave, y dejeκ ser la curvatura de la curva enP. Un círculo que:
- pasa a travésP,
- se encuentra en el lado cóncavo deC,
- tiene una línea tangente común comoC enP y
- tiene radior=1/κ (por lo tanto tiene curvaturaκ)
es el círculo osculante, o círculo de curvatura, aC atP, yr es el radio de curvatura. La figura11.5.4 muestra la gráfica de la curva vista anteriormente en la figura 11.30 y sus círculos osculantes enA yB. Un giro brusco corresponde a un círculo con un radio pequeño; un giro gradual corresponde a un círculo con un radio grande. Poder pensar en curvatura en términos del radio de un círculo es muy útil.
Ejemplo11.5.4: Finding curvature
Encuentra la curvatura de la parábola definida pory=x2 en el vértice y enx=1.
Solución
Utilizamos la primera fórmula que se encuentra en el Teorema 100.
\ [\ begin {align*}
\ kappa (x) &=\ dfrac {|2|} {\ grande (1+ (2x) ^2\ grande) ^ {3/2}}\\ [4pt]
&=\ dfrac2 {\ grande (1+4x^2\ grande) ^ {3/2}}.
\ end {alinear*}\]
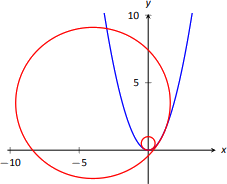
En el vértice (x=0), la curvatura esκ=2. Atx=1, la curvatura esκ=2/(5)3/2≈0.179. Así enx=0, la curvatura dey=x2 es la de un círculo de radio1/2; atx=1, la curvatura es la de un círculo con radio≈1/0.179≈5.59. Esto se ilustra en la Figura11.5.5. Atx=3, la curvatura es0.009; la gráfica es casi recta ya que la curvatura es muy cercana a 0.
Ejemplo\PageIndex{5}: Finding curvature
Encuentra dónde se maximiza\vecs r(t) = \langle t, t^2, 2t^3\rangle la curvatura de.
Solución
Utilizamos la tercera fórmula en el Teorema 100 como\vecs r (t) se define en el espacio. Dejamos al lector verificar que
\vecs r ^\prime(t) =\langle 1,2t,6t^2\rangle,\quad \vecs r^{\prime\prime}(t) = \langle 0,2,12t\rangle,\quad \text{and}\quad \vecs r ^\prime(t)\times \vecs r^{\prime\prime}(t) = \langle 12t^2,-12t,2\rangle.
Así
\ [\ begin {align*}
\ kappa (t) &=\ dfrac {\ norm {\ vecs r ^\ prime (t)\ veces\ vecs r^ {\ prime\ prime} (t)}} {\ norm {\ vecs r ^\ prime (t)} ^3}\\ [4pt]
&=\ dfrac {\ norm {\ langle 12t^2, t,2\ rangle}} {\ norma {\ langle 1,2t,6t^2\ rangle} ^3}\\ [4pt]
&=\ dfrac {\ sqrt {144t^4+144t^2+4}} {\ izquierda (\ sqrt {1+4t^2+36t^4\}\ derecha) ^3}
\ final {alinear*}\]
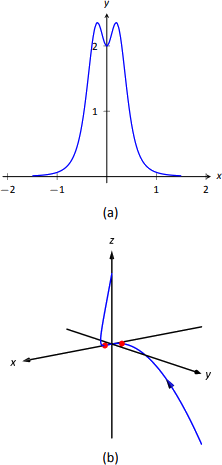
Si bien esta no es una fórmula particularmente “agradable”, sí nos dice explícitamente cuál es la curvatura en unt valor dado. Para maximizar\kappa(t), debemos resolver\kappa'(t)=0 parat. Esto es factible, pero consume mucho tiempo. En su lugar, considere la gráfica de\kappa(t) como se da en la Figura\PageIndex{6a}. Vemos que\kappa se maximiza en dost valores; usando un solucionador numérico, encontramos que estos valores sont\approx\pm 0.189. En la Figura\PageIndex{1b} graficamos\vecs r (t) e indicamos los puntos donde se maximiza la curvatura.
Curvatura y movimiento
Dejar\vecs r(t) ser una función de posición de un objeto, con velocidad\vecs v (t) = \vecs r ^\prime(t) y aceleración\vecs a(t)=\vecs r^{\prime\prime}(t). En la Sección 11.4 establecimos que la aceleración está en el plano formado por\vecs T(t) y\vecs N(t), y que podemos encontrar escalaresa_\text{T} ya_\text{N} tales que
\vecs a (t) = a_\text{T}\vecs T(t) + a_\text{N}\vecs N(t).
El teorema 98 da fórmulas paraa_\text{T} ya_\text{N}:
a_\text{T} = \dfrac{d}{dt}\Big(\norm{\vecs v (t) }\Big) \quad \text{and} \quad a_\text{N} = \dfrac{\norm{\vecs v (t) \times \vecs a (t) }}{\norm{\vecs v (t) }}.
Entendimos que la cantidad de aceleración en la dirección de\vecs T se relaciona únicamente con cómo está cambiando la velocidad del objeto, y que la cantidad de aceleración en la dirección de\vecs N se relaciona con cómo está cambiando la dirección de desplazamiento del objeto. (Es decir, si el objeto viaja a velocidad constante,a_\text{T}=0; si el objeto viaja en una dirección constante,a_\text{N}=0.)
En la Ecuación\ ref {eq:vvfarc3} al inicio de esta sección, encontramoss\,'(t) = \norm{\vecs v (t) }. Podemos combinar este hecho con la fórmula anteriora_\text{T} para escribir
a_\text{T} = \dfrac{d}{dt}\Big(\norm{\vecs v (t) }\Big) = \dfrac{d}{dt}\big( s\,'(t)\big) = s\,''(t).
Ya ques\,'(t) es la velocidad,s\,''(t) es la velocidad a la que la velocidad está cambiando con respecto al tiempo. Vemos una vez más que el componente de aceleración en la dirección de desplazamiento se relaciona únicamente con la velocidad, no con un cambio de dirección.
Ahora compara la fórmula paraa_\text{N} arriba con la fórmula para curvatura en el Teorema 100:
a_\text{N} = \dfrac{\norm{\vecs v (t) \times \vecs a (t) }}{\norm{\vecs v (t) }}\quad \text{and}\quad \kappa = \dfrac{\norm{\vecs r ^\prime(t)\times\vecs r^{\prime\prime}(t)}}{\norm{\vecs r ^\prime(t)}^3}=\dfrac{\norm{\vecs v (t) \times \vecs a (t) }}{\norm{\vecs v (t) }^3} .
Así
\ [\ begin {align}
a_\ text {N} &=\ kappa\ norm {\ vecs v (t)} ^2\ label {eq:curvature_an}\\ [4pt]
&=\ kappa\ Grande (s\, '(t)\ Grande) ^2\ nonumber
\ end {align}\]
Esta última ecuación muestra que el componente de aceleración que cambia la dirección del objeto depende de dos cosas: la curvatura de la trayectoria y la velocidad del objeto.
Imagínese conducir un automóvil en un círculo en sentido horario. Naturalmente sentirás una fuerza empujándote hacia la puerta (con mayor precisión, la puerta te está empujando a medida que el auto gira y quieres viajar en línea recta). Si mantienes constante el radio del círculo pero aceleras (es decir, aumentandos\,'(t)), la puerta empuja más fuerte contra ti (a_\text{N}ha aumentado). Si mantienes tu velocidad constante pero aprietas el giro (es decir, aumentas\kappa), una vez más la puerta te empujará más fuerte.
Poniendo nuestras nuevas fórmulas paraa_\text{T} ya_\text{N} juntas, tenemos
\vecs a (t) = s\,''(t)\vecs T(t) + \kappa\norm{\vecs v (t) }^2\vecs N(t).
Esta no es una forma particularmente práctica de encontrara_\text{T} ya_\text{N}, pero revela algunos grandes conceptos sobre cómo la aceleración interactúa con la velocidad y la forma de una curva.
Ejemplo\PageIndex{6}: Curvature and road design
El radio mínimo de la curva en una hoja de trébol de carretera está determinado por la velocidad de operación, como se indica en la tabla de la Figura\PageIndex{7}. Para cada curva y velocidad, cómpulea_\text{N}.
Solución
Usando la ecuación\ ref {eq:curvature_an}, podemos calcular la aceleración normal a la curva en cada caso. Comenzamos convirtiendo cada velocidad de “millas por hora” a “pies por segundo” multiplicando por5280/3600.
\ [\ begin {align*}
\ text {35mph, 310ft} &\ Rightarrow 51.33\ texto {ft/s},\ quad\ kappa = 1/310\\ [4pt]
a_\ text {N} &=\ kappa\ norma {\ vecs v (t)} ^2\\ [4pt]
&=\ dfrac1 {310}\ grande (51.33\ grande) 2\\ [4pt]
&= 8.50\ texto {ft/s} ^2.
\ end {alinear*}\]
\ [\ begin {align*}
\ text {40mph, 430ft} &\ Rightarrow 58.67\ text {ft/s},\ quad\ kappa = 1/430\\ [4pt]
a_\ text {N} &=\ dfrac1 {430}\ big (58.67\ big) ^2\\ [4pt]
&= 8.00\ text {ft/s} ^2.
\ end {alinear*}\]
\ [\ begin {align*}
\ text {45mph,540ft} &\ Rightarrow 66\ text {ft/s},\ quad\ kappa = 1/540\\ [4pt]
a_\ text {N} &=\ dfrac1 {540}\ big (66\ big) ^2\\ [4pt]
&= 8.07\ text {ft/s} ^2.
\ end {alinear*}\]
Tenga en cuenta que cada aceleración es similar; esto es por diseño. Considerando la fórmula clásica de “\timesAceleración de= masa forzada”, esta aceleración debe mantenerse pequeña para que las llantas de un vehículo mantengan un “agarre” en la carretera. Si uno viaja en un giro de radio de 310 pies a una velocidad de 50 mph, la aceleración es el doble, a 17.35 pies/s^2. Si la aceleración es demasiado alta, la fuerza de fricción creada por las llantas puede no ser suficiente para evitar que el automóvil se deslice. Los ingenieros civiles computan rutinariamente una velocidad de diseño “segura”, luego restan 5-10 mph para crear el límite de velocidad publicado para mayor seguridad.
Terminamos este capítulo con una reflexión sobre lo que hemos cubierto. Comenzamos con funciones de valor vectorial, que en su momento pueden haber parecido ser solo otra forma de escribir ecuaciones paramétricas. Sin embargo, hemos visto que la perspectiva vectorial nos ha dado una gran penetración en el comportamiento de las funciones y el estudio del movimiento. Las funciones de posición con valor vectorial transmiten información de desplazamiento, distancia recorrida, velocidad, velocidad, aceleración y curvatura, cada una de las cuales tiene gran importancia en la ciencia y la ingeniería.


