12.8: Valores extremos

Última actualización
Guardar como PDF

Page ID: 111771

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Dada una función$z=f(x,y)$, a menudo nos interesan los puntos donde$z$ toma los valores más grandes o más pequeños. Por ejemplo, si$z$ representa una función de costo, probablemente querríamos saber qué$(x,y)$ valores minimizan el costo. Si$z$ representa la relación de un volumen a la superficie, probablemente querríamos saber dónde$z$ es mayor. Esto lleva a la siguiente definición.

Definición 97 Extrema Relativa y Absoluta

Dejar$z=f(x,y)$ definirse en un conjunto$S$ que contenga el punto$P=(x_0,y_0)$.

Si hay un disco abierto que$D$ contiene$P$ tal que$f(x_0,y_0) \geq f(x,y)$ para all$(x,y)$ in$D$, entonces$f$ tiene un máximo relativo en$P$; si$f(x_0,y_0) \leq f(x,y)$ para all$(x,y)$ in$D$, entonces$f$ tiene un mínimo relativo en$P$.
Si$f(x_0,y_0)\geq f(x,y)$ para todos$(x,y)$ adentro$S$, entonces$f$ tiene un máximo absoluto en$P$; si$f(x_0,y_0)\leq f(x,y)$ para todos$(x,y)$ adentro$S$, entonces$f$ tiene un mínimo absoluto en$P$.
Si$f$ tiene un máximo o mínimo relativo en$P$, entonces$f$ tiene un extremo relativo at$P$; si$f$ tiene un máximo absoluto o mínimo at$P$, entonces$f$ tiene un extremo absoluto at$P$.

Si$f$ tiene un máximo relativo o absoluto en$P=(x_0,y_0)$, significa que cada curva en la superficie de$f$ through también$P$ tendrá un máximo relativo o absoluto at$P$. Recordando lo que aprendimos en la Sección 3.1, las pendientes de las líneas tangentes a estas curvas en$P$ deben ser 0 o indefinidas. Dado que las derivadas direccionales se calculan utilizando$f_x$ y$f_y$, nos llevan a la siguiente definición y teorema.

Definición 98 Punto crítico

Dejar$z = f(x,y)$ ser continuo en un juego abierto$S$. Un punto crítico$P=(x_0,y_0)$ de$f$ es un punto en$S$ tal que

$f_x(x_0,y_0) = 0$y$f_y(x_0,y_0) = 0$, o
$f_x(x_0,y_0)$y/o$f_y(x_0,y_0)$ está indefinido.

teorema 114 Puntos Críticos y Extremos Relativos

Dejar$z=f(x,y)$ ser definido en un conjunto abierto$S$ que contiene$P=(x_0,y_0)$. Si$f$ tiene un extremo relativo en$P$, entonces$P$ es un punto crítico de$f$.

Por lo tanto, para encontrar extremos relativos, encontramos los puntos críticos$f$ y determinamos cuáles corresponden a máximos relativos, mínimos relativos, o ninguno de ellos. Los siguientes ejemplos demuestran este proceso.

Ejemplo$\PageIndex{1}$: Finding critical points and relative extrema

Vamos$f(x,y) = x^2+y^2-xy-x-2$. Encuentra los extremos relativos de$f$.

Solución

Comenzamos por computar las derivadas parciales de$f$:

\[f_x(x,y) = 2x-y-1 \qquad \text{and}\qquad f_y(x,y) = 2y-x.\]

Cada uno nunca es indefinido. Un punto crítico ocurre cuando$f_x$ y$f_y$ son simultáneamente 0, llevándonos a resolver el siguiente sistema de ecuaciones lineales:

\[2x-y-1 = 0\qquad \text{and}\qquad -x+2y = 0.\]

Esta solución a este sistema es$x=2/3$,$y=1/3$. (Compruebe que en$(2/3,1/3)$, ambos$f_x$ y$f_y$ son 0.)

Figura 12.27: La superficie en el Ejemplo 12.8.1 con su mínimo absoluto indicado.

La gráfica de la Figura 12.27 muestra$f$ junto con este punto crítico. De la gráfica queda claro que se trata de un mínimo relativo; una mayor consideración de la función muestra que éste es en realidad el mínimo absoluto.

Ejemplo$\PageIndex{2}$: Finding critical points and relative extrema

Vamos$f(x,y) = -\sqrt{x^2+y^2}+2$. Encuentra los extremos relativos de$f$.

Solución

Comenzamos por computar las derivadas parciales de$f$:

\[f_x(x,y) = \frac{-x}{\sqrt{x^2+y^2}}\qquad \text{and}\qquad f_y(x,y) = \frac{-y}{\sqrt{x^2+y^2}}.\]

Está claro que$f_x=0$ cuando$x=0$\ &$y\neq0$, y que$f_y=0$ cuando$y=0$\ &$x\neq0$. En$(0,0)$, ambos$f_x$ y no$f_y$ son$0$, sino más bien indefinidos. El punto$(0,0)$ sigue siendo un punto crítico, sin embargo, porque las derivadas parciales son indefinidas. Este es el único punto crítico de$f$.

Figura 12.28: La superficie en el Ejemplo 12.8.2 con su máximo absoluto indicado.

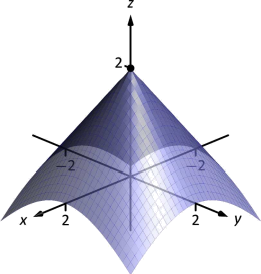
La superficie de$f$ se grafica en la Figura 12.28 junto con el punto$(0,0,2)$. La gráfica muestra que este punto es el máximo absoluto de$f$.

En cada uno de los dos ejemplos anteriores, encontramos un punto crítico de$f$ y luego determinamos si se trataba o no de un máximo o mínimo relativo (o absoluto) mediante la gráfica. Sería bueno poder determinar si un punto crítico correspondía a un máximo o un minuto sin una gráfica. Antes de desarrollar una prueba de este tipo, hacemos un ejemplo más que arroja más luz sobre los temas que nuestra prueba necesita considerar.

Ejemplo$\PageIndex{3}$: Finding critical points and relative extrema

Vamos$f(x,y) = x^3-3x-y^2+4y$. Encuentra los extremos relativos de$f$.

Solución

Una vez más comenzamos por encontrar las derivadas parciales de$f$:

\[f_x(x,y) = 3x^2-3\qquad \text{and} \qquad f_y(x,y) = -2y+4.\]

Cada uno está siempre definido. Estableciendo cada uno igual a 0 y resolviendo para$x$ y$y$, encontramos

\ [\ begin {align*}
f_x (x, y) = 0\ quad &\ Rightarrow x=\ pm 1\\
f_y (x, y) = 0\ quad &\ Rightarrow y = 2.
\ end {alinear*}\]

Tenemos dos puntos críticos:$(-1,2)$ y$(1,2)$. Para determinar si corresponden a un máximo o mínimo relativo, consideramos la gráfica de$f$ la Figura 12.29.

Figura 12.29: La superficie en el Ejemplo 12.8.3 con ambos puntos críticos marcados.

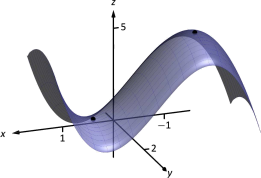
El punto crítico corresponde$(-1,2)$ claramente a un máximo relativo. Sin embargo, el punto crítico en no$(1,2)$ es ni un máximo ni un mínimo, mostrando una característica diferente e interesante.

Si uno camina paralelo al$y$ eje -hacia este punto crítico, entonces este punto se convierte en un máximo relativo a lo largo de este camino. Pero si uno camina hacia este punto paralelo al$x$ eje -eje, este punto se convierte en un mínimo relativo a lo largo de este camino. Un punto que parece actuar tanto como máximo como mínimo es un punto de silla de montar. A continuación se presenta una definición formal.

Definición 99 Punto de Silín

Déjese$P=(x_0,y_0)$ estar en el dominio de$f$ dónde$f_x=0$ y$f_y=0$ en$P$. $P$es un punto de sillín de$f$ si, por cada disco abierto$D$ que contenga$P$, hay puntos$(x_1,y_1)$ y$(x_2,y_2)$ en$D$ tal que$f(x_0,y_0)>f(x_1,y_1)$ y$f(x_0,y_0)<f(x_2,y_2)$.

En un punto de sillín, la velocidad instantánea de cambio en todas las direcciones es 0 y hay puntos cercanos con$z$ valores -menores y mayores que el$z$ -valor del punto de sillín.

Antes del Ejemplo 12.8.3 mencionamos la necesidad de una prueba para diferenciar entre máximos relativos y mínimos. Ahora reconocemos que nuestra prueba también necesita tener en cuenta los puntos de sillín. Para ello, consideramos las segundas derivadas parciales de$f$.

Recordemos que con funciones variables únicas, como$y=f(x)$, si$f''(c)>0$, entonces$f$ es cóncavo hacia arriba en$c$, y si$f'(c) =0$, entonces$f$ tiene un mínimo relativo en$x=c$. (Llamamos a esto la Segunda Prueba Derivada.) Tenga en cuenta que en un punto de silla de montar, parece que la gráfica es “tanto” cóncava hacia arriba como cóncava hacia abajo, dependiendo de la dirección que esté considerando.

Sería bueno que lo siguiente fuera cierto:

$12.8 words.PNG$

Sin embargo, este no es el caso. Las funciones$f$ existen donde$f_{xx}$ y$f_{yy}$ son ambas positivas pero todavía existe un punto de sillín. En tal caso, mientras la concavidad en la$x$ dirección -es hacia arriba (es decir,$f_{xx}>0$) y la concavidad en la$y$ dirección también es hacia arriba (es decir,$f_{yy}>0$), la concavidad cambia en algún lugar entre las direcciones$x$ - y$y$ -direcciones.

Para dar cuenta de esto, considere$D = f_{xx}f_{yy}-f_{xy}f_{yx}$. Dado que$f_{xy}$ y$f_{yx}$ son iguales cuando son continuas (refiérase de nuevo al Teorema 103), podemos reescribir esto como$D = f_{xx}f_{yy}-f_{xy}^{\,2}$. $D$se puede usar para probar si la concavidad en un punto cambia dependiendo de la dirección. Si$D>0$, la concavidad no cambia (es decir, en ese punto, la gráfica es cóncava hacia arriba o hacia abajo en todas las direcciones). Si$D<0$, la concavidad sí cambia. Si$D=0$, nuestra prueba no logra determinar si la concavidad cambia o no. Declaramos el uso de$D$ en el siguiente teorema.

TEOREMA 115 Segunda Prueba Derivada

Dejar$z=f(x,y)$ ser diferenciable en un conjunto abierto que contiene$P = (x_0,y_0)$, y dejar
\[D = f_{xx}(x_0,y_0)f_{yy}(x_0,y_0)-f_{xy}^{\,2}(x_0,y_0).\]

Si$D>0$ y$f_{xx}(x_0,y_0)>0$, entonces$P$ es un mínimo relativo de$f$.
Si$D>0$ y$f_{xx}(x_0,y_0)<0$, entonces$P$ es un máximo relativo de$f$.
Si$D<0$, entonces$P$ es un punto de silla de montar de$f$.
Si$D=0$, la prueba no es concluyente.

Primero practicamos usando esta prueba con la función del ejemplo anterior, donde determinamos visualmente que teníamos un máximo relativo y un punto de sillín.

Ejemplo$\PageIndex{4}$: Using the Second Derivative Test

Que$f(x,y) = x^3-3x-y^2+4y$ como en el Ejemplo 12.8.3. Determine si la función tiene un mínimo relativo, máximo o punto de sillín en cada punto crítico.

Solución
Determinamos previamente que los puntos críticos de$f$ son$(-1,2)$ y$(1,2)$. Para utilizar la Prueba de Segunda Derivada, debemos encontrar las segundas derivadas parciales de$f$:
\[f_{xx} = 6x;\qquad f_{yy} = -2;\qquad f_{xy} = 0.\]
Así$D(x,y) = -12x$.

En$(-1,2)$:$D(-1,2) = 12>0$, y$f_{xx}(-1,2) = -6$. Por la Segunda Prueba Derivada,$f$ tiene un máximo relativo a$(-1,2)$.

En$(1,2)$:$D(1,2) = -12 <0$. La Segunda Prueba Derivada establece que$f$ tiene un punto de sillín en$(1,2)$.

La Segunda Prueba Derivada confirmó lo que determinamos visualmente.

Ejemplo$\PageIndex{5}$: Using the Second Derivative Test

Encuentra los extremos relativos de$f(x,y) = x^2y+y^2+xy$.

Solución

Comenzamos por encontrar la primera y segunda derivadas parciales de$f$:

\ [\ begin {array} {ccc}
f_x = 2xy+y & & f_y = x^2+2y+x\\
f_ {xx} = 2y & f_ {yy} = 2\\
f_ {xy} = 2x+1 & & f_ {yx} = 2x+1.
\ end {array}\]

Encontramos los puntos críticos al encontrar dónde$f_x$ y$f_y$ son simultáneamente 0 (ambos nunca son indefinidos). Ajuste$f_x=0$, contamos con:

\[f_x=0 \quad \Rightarrow \quad 2xy+y=0\quad \Rightarrow \quad y(2x+1)=0.\]

Esto implica que para$f_x=0$, ya sea$y=0$ o$2x+1=0$.

Supongamos$y=0$ entonces considerar$f_y=0$:

\ [\ begin {align*}
f_y &= 0\\
x^2+2y+x &= 0,\ qquad\ text {y ya que$y=0$, tenemos}\\
x^2+x &= 0\\
x (x+1) & = 0.
\ end {alinear*}\]

Así si$y=0$, tenemos cualquiera$x=0$ o$x=-1$, dando dos puntos críticos:$(-1,0)$ y$(0,0)$.

Volviendo a$f_x$, ahora asumir$2x+1=0$, es decir, eso$x=-1/2$, luego considerar$f_y=0$:

\ [\ begin {align*}
f_y &= 0\\
x^2+2y+x &= 0,\ qquad\ text {y ya que$x=-1/2$, tenemos}\\
1/4+2y-1/2 &= 0\\
y&= 1/8.
\ end {alinear*}\]

Así si$x=-1/2$,$y=1/8$ dando el punto crítico$(-1/2,1/8)$.

Con$D = 4y-(2x+1)^2$, aplicamos la Prueba de Segunda Derivada a cada punto crítico.

A$(-1,0)$,$D <0$, así$(-1,0)$ es un punto de silla de montar.

A$(0,0)$,$D<0$, también lo$(0,0)$ es un punto de silla de montar.

En$(-1/2,1/8)$,$D>0$ y$f_{xx} > 0$, así$(-1/2,1/8)$ es un mínimo relativo.

Figura 12.30: Gráfica$f$ del Ejemplo 12.8.5 y sus extremos relativos.

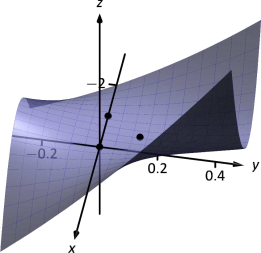
La Figura 12.30 muestra una gráfica de$f$ y los tres puntos críticos. Observe cómo esta función no varía mucho cerca de los puntos críticos —es decir, visualmente es difícil determinar si un punto es un punto de sillín o un mínimo relativo (¡o incluso un punto crítico en absoluto!). Esta es una de las razones por las que es tan importante tener la Prueba de Segunda Derivada.

Optimización restringida

Al optimizar funciones de una variable como$y=f(x)$, hicimos uso del Teorema 25, el Teorema del Valor Extremo, que decía que a lo largo de un intervalo cerrado$I$, una función continua tiene tanto un valor máximo como mínimo. Para encontrar estos valores máximos y mínimos, evaluamos$f$ en todos los puntos críticos del intervalo, así como en los puntos finales (el “límite”) del intervalo.

Un teorema y procedimiento similar se aplica a las funciones de dos variables. Una función continua sobre un conjunto cerrado también alcanza un valor máximo y mínimo (ver el siguiente teorema). Podemos encontrar estos valores evaluando la función en los valores críticos en el conjunto y sobre el límite del conjunto. Después de afirmar formalmente este teorema de valor extremo, damos ejemplos.

teorema 116 Teorema de Valor Extremo

Let$z=f(x,y)$ Ser una función continua en un conjunto cerrado y acotado$S$. Entonces$f$ tiene un valor máximo y mínimo encendido$S$.

Ejemplo$\PageIndex{6}$: Finding extrema on a closed set

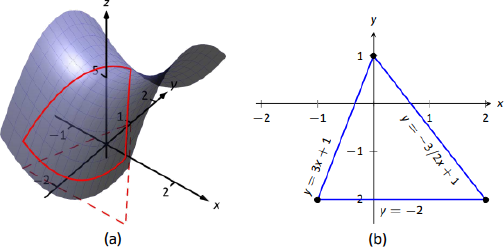
Dejar$f(x,y) = x^2-y^2+5$ y dejar$S$ ser el triángulo con vértices$(-1,-2)$,$(0,1)$ y$(2,-2)$. Encuentra los valores máximos y mínimos de$f$ on$S$.

Solución
Puede ayudar a ver una gráfica de$f$ junto con el conjunto$S$. En la Figura 12.31 (a) la definición del triángulo$S$ se muestra en el$xy$ plano -en línea discontinua. Por encima de ella está la superficie de$f$; sólo nos preocupa la porción de$f$ encerrada por el “triángulo” en su superficie.

Figura 12.31: Trazando la superficie de$f$ junto con el dominio restringido S.

Comenzamos por encontrar los puntos críticos de$f$. Con$f_x = 2x$ y$f_y = -2y$, nos encontramos con un solo punto crítico, a$(0,0)$.

Ahora encontramos los valores máximos y mínimos que$f$ alcanzan a lo largo del límite de$S$, es decir, a lo largo de los bordes del triángulo. En la Figura 12.31 (b) vemos el triángulo esbozado en el plano con las ecuaciones de las líneas que forman sus aristas etiquetadas.

Comience con el borde inferior, a lo largo de la línea$y=-2$. Si$y$ es$-2$ así, entonces en la superficie, estamos considerando puntos$f(x,-2)$; es decir, nuestra función se reduce a$f(x,-2) = x^2-(-2)^2+5 = x^2+1=f_1(x)$. Queremos maximizar/minimizar$f_1(x)=x^2+1$ en el intervalo$[-1,2]$. Para ello, evaluamos$f_1(x)$ en sus puntos críticos y en los puntos finales.

Los puntos críticos de$f_1$ se encuentran estableciendo su derivada igual a 0:
\[f'_1(x)=0\qquad \Rightarrow x=0.\]
Evaluando$f_1$ en este punto crítico, y en los puntos finales de$[-1,2]$ da:
\ [\ begin {align*}
f_1 (-1) = 2\ qquad&\ Rightarrow\ qquad f (-1, -2) = 2\\
f_1 (0) = 1\ qquad&\ Rightarrow\ qquad f (0, -2) = 1\\
f_1 (2) = 5\ qquad&\ Rightarrow\ qquad f (2, -2) = 5.
\ end {align*}\]
Observe cómo evaluar$f_1$ en un punto es lo mismo que evaluar$f$ en su punto correspondiente.

Tenemos que hacer este proceso dos veces más, para los otros dos bordes del triángulo.

A lo largo del borde izquierdo, a lo largo de la línea$y=3x+1$,$3x+1$
\[f(x,y) = f(x,3x+1) = x^2-(3x+1)^2+5 = -8x^2-6x+4 = f_2(x).\]
sustituimos$y$ en$f(x,y)$: Queremos los valores máximo y mínimo de$f_2$ en el intervalo$[-1,0]$, así evaluamos$f_2$ en sus puntos críticos y los puntos finales de la intervalo. Encontramos los puntos críticos:
\[f'_2(x) = -16x-6=0 \qquad \Rightarrow \qquad x=-3/8.\]

Evaluar$f_2$ en su punto crítico y los puntos finales de$[-1,0]$:
\ [\ begin {align*}
f_2 (-1) = 2\ qquad&\ Rightarrow\ qquad f (-1, -2) = 2\\
f_2 (-3/8) = 41/8=5.125\ qquad&\ Rightarrow\ qquad f (-3/8, -0.125) = 5.125\\
f_2 (0) = 1\ qquad&\ Rightarrow\ qquad f (0,1) = 4.
\ end {alinear*}\]

Finalmente, evaluamos$f$ a lo largo del borde derecho del triángulo, donde$y = -3/2x+1$.
\[f(x,y) = f(x,-3/2x+1) = x^2-(-3/2x+1)^2+5 = -\frac54x^2+3x+4=f_3(x).\]
Los puntos críticos de$f_3(x)$ son:
\[f'_3(x) = 0 \qquad \Rightarrow \qquad x=6/5=1.2.\]
Evaluamos$f_3$ en este punto crítico y en los puntos finales del intervalo$[0,2]$:
\ [\ begin {align*}
f_3 (0) = 4\ qquad&\ Rightarrow\ qquad f (0,1) = 4\\
f_3 (1.2) = 5.8\ qquad&\ Rightarrow\ qquad f (1.2, -0.8) = 5.8\\
f_3 (2) = 5\ qquad&\ Rightarrow\ qquad f (2, -2) = 5.
\ end {align*}\]
Un último punto a probar: el punto crítico de$f$,$(0,0)$. Nos encontramos$f(0,0) = 5$.

Figura 12.32: La superficie de$f$ junto con puntos importantes a lo largo del límite de S y el interior.

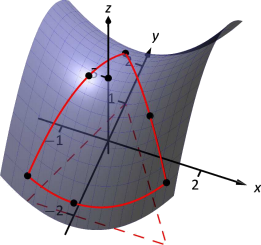
Hemos evaluado$f$ en un total de 7 lugares diferentes, todos ellos mostrados en la Figura 12.32. Comprobamos cada vértice del triángulo dos veces, ya que cada uno se mostró como el punto final de un intervalo dos veces. De todos los$z$ valores -encontrados, el máximo es 5.8, encontrado en$(1.2,-0.8)$; el mínimo es 1, encontrado en$(0,-2)$.

Esta parte del texto se titula “Optimización restringida” porque queremos optimizar una función (es decir, encontrar sus valores máximos y/o mínimos) sujeta a una restricción, límites en los que se consideran los puntos de entrada. En el ejemplo anterior, nos limitamos al considerar una función solo dentro del límite de un triángulo. Esto fue en gran parte arbitrario; la función y el límite se eligieron solo como ejemplo, sin un “significado” real detrás de la función o la restricción elegida.

Sin embargo, resolver problemas de optimización restringida es un tema muy importante en las matemáticas aplicadas. Las técnicas que aquí se desarrollan son la base para resolver problemas mayores, donde intervienen más de dos variables.

Ilustramos la técnica una vez más con un problema clásico.

Ejemplo$\PageIndex{7}$: Constrained Optimization

El Servicio Postal de los Estados Unidos establece que la circunferencia y la longitud del Paquete Postal Estándar no deben exceder de 130". Dada una caja rectangular, el “largo” es el lado más largo, y la “circunferencia” es el doble del ancho+alto.

Dada una caja rectangular donde la anchura y la altura son iguales, ¿cuáles son las dimensiones de la caja que dan el volumen máximo sujeto a la restricción del tamaño de un Paquete Post Estándar?

Solución

Dejar$w$,$h$ y$\ell$ denotar el ancho, alto y largo de una caja rectangular; suponemos aquí que$w=h$. La cordura es entonces$2(w+h) = 4w$. El volumen de la caja es$V(w,\ell) = wh\ell = w^2\ell$. Deseamos maximizar este volumen sujeto a la restricción$4w+\ell\leq 130$, o$\ell\leq 130-4w$. (El sentido común también indica que$\ell>0, w>0$.)

Comenzamos por encontrar los valores críticos de$V$. Nos encontramos con eso$V_w = 2w\ell$ y$V_\ell = w^2$; estos son simultáneamente 0 solo en$(0,0)$. Esto da un volumen de 0, por lo que podemos ignorar este punto crítico.

Consideramos ahora el volumen a lo largo de la restricción$\ell=130-4w.$ A lo largo de esta línea, tenemos:
\[V(w,\ell) = V(w,130-4w) = w^2(130-4w) = 130w^2-4w^3 = V_1(w).\]
La restricción es aplicable en el$w$ -intervalo$[0,32.5]$ como se indica en la figura. Así queremos maximizar$V_1$ en$[0,32.5]$.

Al encontrar los valores críticos de$V_1$, tomamos la derivada y la establecemos igual a 0:
\[V\,'_1(w) = 260w-12w^2 = 0 \quad \Rightarrow \quad w(260-12w)= 0 \quad \Rightarrow \quad w=0,\frac{260}{12}\approx 21.67.\]

Encontramos dos valores críticos: cuándo$w=0$ y cuándo$w=21.67$. Nuevamente ignoramos la$w=0$ solución; el volumen máximo, sujeto a la restricción, viene a$w=h=21.67$,$\ell = 130-4(21.6) =43.33.$ Esto da un volumen de$V(21.67,43.33) \approx 19,408$ in$^3$.

Figura 12.33: Graficando el volumen de una caja con circunferencia 4w y longitud$l$, sujeto a una restricción de tamaño.

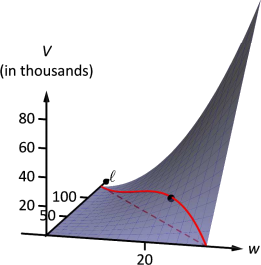
La función de volumen$V(w,\ell)$ se muestra en la Figura 12.33 junto con la restricción$\ell = 130-4w$. Como se hizo anteriormente, la restricción se dibuja discontinua en el$xy$ plano -y también a lo largo de la superficie de la función. Se indica el punto donde se maximiza el volumen.

Es difícil exagerar la importancia de la optimización. En “el mundo real”, buscamos rutinariamente hacer algo mejor. Al expresar el algo como una función matemática, “hacer algo mejor” significa “optimizar alguna función”.

Las técnicas que aquí se muestran son solo el comienzo de un campo increíblemente importante. Muchas funciones que buscamos optimizar son increíblemente complejas, haciendo que el paso de “encontrar el gradiente y fijarlo igual a$\vec 0$" sea altamente no trivial. El dominio de los principios aquí es clave para poder abordar estos problemas más complicados.

Colaboradores y Atribuciones

Template:ContribApexCalc