2.5: La definición precisa de un límite
- Page ID
- 116873
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Describir la definición épsilon-delta de un límite.
- Aplicar la definición épsilon-delta para encontrar el límite de una función.
- Describir las definiciones épsilon-delta de límites unilaterales e infinitos.
- Utilice la definición épsilon-delta para probar las leyes de límite.
A estas alturas ya se ha avanzado de la definición muy informal de un límite en la introducción de este capítulo a la comprensión intuitiva de un límite. En este punto, debes tener un sentido intuitivo muy fuerte de lo que significa el límite de una función y cómo puedes encontrarla. En esta sección, convertimos esta idea intuitiva de un límite en una definición formal utilizando lenguaje matemático preciso. La definición formal de un límite es posiblemente una de las definiciones más desafiantes que encontrarás al principio de tu estudio del cálculo; sin embargo, merece la pena cualquier esfuerzo que hagas para conciliarlo con tu noción intuitiva de límite. Entender esta definición es la clave que abre la puerta a una mejor comprensión del cálculo.
Cuantificación de la cercanía
Antes de exponer la definición formal de un límite, debemos introducir algunas ideas preliminares. Recordemos que la distancia entre dos puntos\(a\) y\(b\) en una recta numérica viene dada por |\(a−b\) |.
- La declaración |\(f(x)−L |<ε\) puede interpretarse como: La distancia entre\(f(x)\) y\(L\) es menor que\(ε\).
- La declaración\(0<|x−a|<δ\) puede interpretarse como:\(x≠a\) y la distancia entre\(x\) y\(a\) es menor que\(δ\).
También es importante observar las siguientes equivalencias para el valor absoluto:
- La declaración |\(f(x)−L|<ε\) es equivalente a la declaración\(L−ε<f(x)<L+ε\).
- El enunciado\(0<|x−a|<δ\) es equivalente al enunciado\(a−δ<x<a+δ\) y\(x≠a\).
Con estas aclaraciones, podemos exponer la definición formal épsilon-delta del límite.
Dejar\(f(x)\) ser definido para todo\(x≠a\) lo largo de un intervalo abierto que contiene\(a\). \(L\)Déjese ser un número real. Entonces
\[\lim_{x→a}f(x)=L \nonumber \]
si, por cada\(ε>0\), existe un\(δ>0\), tal que si\(0<|x−a|<δ\), entonces\(|f(x)−L|<ε\).
Esta definición puede parecer bastante compleja desde un punto de vista matemático, pero se vuelve más fácil de entender si la desglosamos frase por frase. El enunciado en sí implica algo llamado cuantificador universal (para cada uno\(ε>0\)), un cuantificador existencial (existe a\(δ>0\)), y, por último, una declaración condicional (si\(0<|x−a|<δ\), entonces\(|f(x)−L|<ε)\). Echemos un vistazo a Table\(\PageIndex{1}\), que desglosa la definición y traduce cada parte.
| Definición | Traducción |
|---|---|
| 1. Para cada\(ε>0\), | 1. Por cada distancia positiva\(ε\) de\(L\), |
| 2. existe un\(δ>0\), | 2. Hay una distancia positiva\(δ\) de\(a\), |
| 3. tal que | 3. tal que |
| 4. si\(0<|x−a|<δ\), entonces\(|f(x)−L|<ε\). | 4. si\(x\) está más cerca que\(δ\) a\(a\) y\(x≠a\), entonces\(f(x)\) está más cerca que\(ε\) a\(L\). |
Podemos obtener un mejor manejo de esta definición observando la definición geométricamente. La figura\(\PageIndex{1}\) muestra los posibles valores de\(δ\) para varias elecciones de\(ε>0\) para una función dada\(f(x)\), un número\(a\) y un límite\(L\) en\(a\). Observe que a medida que elegimos valores más pequeños de\(ε\) (la distancia entre la función y el límite), siempre podemos encontrar\(δ\) uno lo suficientemente pequeño como para que si hemos elegido un\(x\) valor dentro\(δ\) de\(a\), entonces el valor de\(f(x)\) está dentro\(ε\) del límite \(L\).
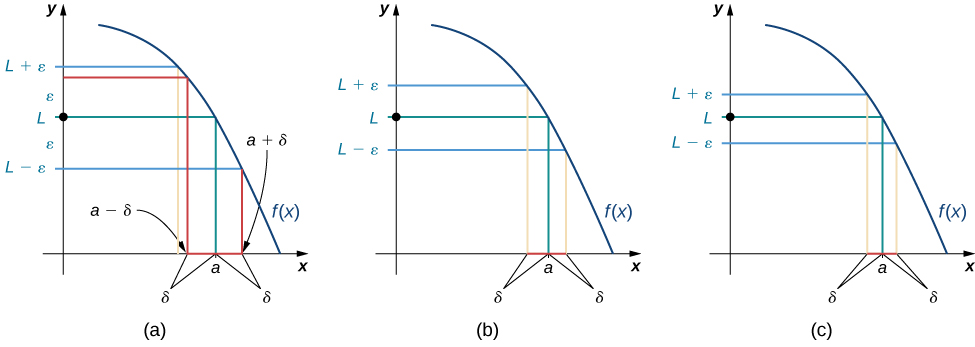
Visite el siguiente applet para experimentar con la búsqueda de valores de\(δ\) para valores seleccionados de\(ε\):
Ejemplo\(\PageIndex{1}\) muestra cómo se puede utilizar esta definición para probar una declaración sobre el límite de una función específica en un valor especificado.
\(\displaystyle \lim_{x→1} \;(2x+1)=3\)Demuéstralo.
Solución
Vamos\(ε>0\).
La primera parte de la definición comienza “Para cada\(ε>0\)” Esto significa que debemos probar que lo que sigue es cierto sin importar el valor positivo de que\(ε\) se elija. Al decir “Vamos”\(ε>0\), señalamos nuestra intención de hacerlo.
Escoge\(δ=\frac{ε}{2}\).
La definición continúa con “existe una”\(δ>0\). La frase “existe” en una declaración matemática es siempre una señal para una búsqueda del tesoro. En otras palabras, debemos ir a buscar\(δ\). Entonces, ¿de dónde\(δ=ε/2\) salió exactamente? Hay dos enfoques básicos para rastrear\(δ\). Un método es puramente algebraico y el otro es geométrico.
Comenzamos abordando el problema desde un punto de vista algebraico. Ya que en última instancia queremos\(|(2x+1)−3|<ε\), comenzamos por manipular esta expresión:\(|(2x+1)−3|<ε\) es equivalente a\(|2x−2|<ε\), que a su vez es equivalente a\(|2||x−1|<ε\). Por último, esto equivale a\(|x−1|<ε/2\). Así, parecería que\(δ=ε/2\) es apropiado.
También podemos encontrar\(δ\) a través de métodos geométricos. La figura\(\PageIndex{2}\) demuestra cómo se hace esto.
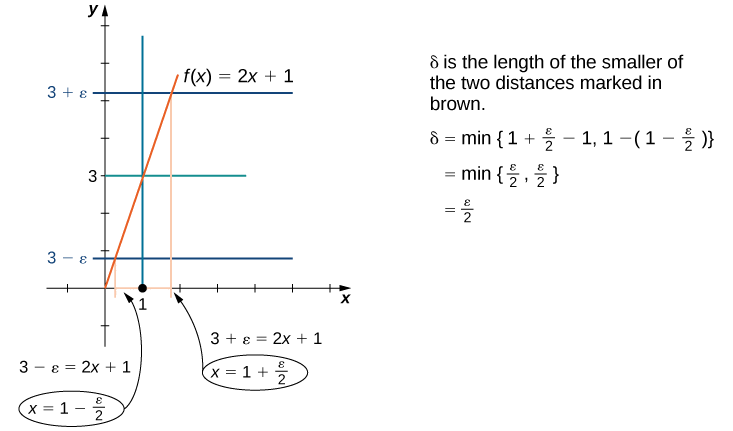
Asumir\(0<|x−1|<δ\). Cuando se\(δ\) ha elegido, nuestro objetivo es demostrar que si\(0<|x−1|<δ\), entonces\(|(2x+1)−3|<ε\). Para probar cualquier enunciado de la forma “Si esto, entonces aquello”, comenzamos asumiendo “esto” y tratando de obtener “eso”.
Por lo tanto,
\(|(2x+1)−3|=|2x−2|\)propiedad de valor absoluto
\(=|2(x−1)|\)
\(=|2||x−1|\)\(|2|=2\)
\(=2|x−1|\)
\(<2⋅δ \)aquí es donde usamos la suposición de que\(0<|x−1|<δ\)
\(=2⋅\frac{ε}{2}=ε\)aquí es donde usamos nuestra elección de\(δ=ε/2\)
Análisis
En esta parte de la prueba, empezamos con\(|(2x+1)−3|\) y utilizamos nuestra suposición\(0<|x−1|<δ\) en una parte clave de la cadena de desigualdades para llegar\(|(2x+1)−3|\) a ser menos que ε. Podríamos haber manipulado fácilmente la supuesta desigualdad\(0<|x−1|<δ\) para llegar de la\(|(2x+1)−3|<ε\) siguiente manera:
\(0<|x−1|<δ⇒|x−1|<δ\)
\(⇒−δ<x−1<δ\)
\(⇒−\frac{ε}{2}<x−1<\frac{ε}{2}\)
\(⇒−ε<2x−2<ε\)
\(⇒|2x−2|<ε\)
\(⇒|(2x+1)−3|<ε.\)
Por lo tanto,\(\displaystyle \lim_{x→1} \;(2x+1)=3.\) (Una vez concluida la prueba, declaramos lo que hemos logrado.)
Después de eliminar todas las observaciones, aquí hay una versión final de la prueba:
Vamos\(ε>0\).
Escoge\(δ=ε/2\).
Asumir\(0<|x−1|<δ\).
Por lo tanto,
\ (\ begin {alinear*} | (2x+1) −3| &= |2x−2|\\ [4pt]
&=|2 (x−1) |\\ [4pt]
&=|2||x−1|\\ [4pt]
&=2|x−1|\\ [4pt]
&<2δ\ [4pt]
&=2⋅\ frac ε} {2}\\ [4pt]
&=ε. \ end {alinear*}\)
Por lo tanto,\(\displaystyle \lim_{x→1} \;(2x+1)=3\).
La siguiente Estrategia de Resolución de Problemas resume el tipo de prueba que elaboramos en Ejemplo\(\PageIndex{1}\).
- Comencemos la prueba con la siguiente declaración: Vamos\(ε>0\).
- A continuación, necesitamos obtener un valor para\(δ\). Después de haber obtenido este valor, hacemos la siguiente declaración, rellenando el espacio en blanco con nuestra elección de\(δ\): Elija\(δ=\) _______.
- El siguiente enunciado en la prueba debe ser (en este punto, rellenamos nuestro valor dado para\(a\)): Asumir\(0<|x−a|<δ\).
- A continuación, con base en esta suposición, necesitamos mostrar eso\(|f(x)−L|<ε\), dónde\(f(x)\) y\(L\) están nuestra función\(f(x)\) y nuestro límite\(L\). En algún momento, necesitamos usar\(0<|x−a|<δ\).
- Concluimos nuestra prueba con la declaración: Por lo tanto,\(\displaystyle \lim_{x→a}f(x)=L\).
Completa la prueba de que\(\displaystyle \lim_{x→−1}\;(4x+1)=−3\) rellenando los espacios en blanco.
Vamos _____.
Elija\(δ=\) _______.
Supongamos\(0<|x\) −_______|\(<δ\).
Así, |________−________|=_____________________________________\(ε\).
Solución
Comenzamos rellenando los espacios en blanco donde las elecciones son especificadas por la definición. Por lo tanto, tenemos
Vamos\(ε>0\).
Elija\(δ\) =_______.
Asumir\(0<|x−(−1)|<δ\). (o equivalentemente,\(0<|x+1|<δ\).)
Así,\(|(4x+1)−(−3)|=|4x+4|=|4||x+1|<4δ\) _______\(ε\).
Centrándonos en la línea final de la prueba, vemos que debemos elegir\(δ=\frac{ε}{4}\).
Ahora completamos la redacción final de la prueba:
Vamos\(ε>0\).
Escoge\(δ=\frac{ε}{4}\).
Asumir\(0<|x−(−1)|<δ\) (o equivalentemente,\(0<|x+1|<δ\).)
Por lo tanto,\(|(4x+1)−(−3)|=|4x+4|=|4||x+1|<4δ=4(ε/4)=ε\).
Completa la prueba de que\(\displaystyle \lim_{x→2}\;(3x−2)=4\) rellenando los espacios en blanco.
Vamos _______.
Elija\(δ\) =_______.
Supongamos\(0<|x−\) ____\(|<\) ____.
Por lo tanto,
|_______−____|\(=\) ______________________________\(ε\).
Por lo tanto,\(\displaystyle \lim_{x→2}\;(3x−2)=4\).
- Pista
-
Siga el esquema en la Estrategia de Resolución de Problemas que elaboramos en su totalidad en Ejemplo\(\PageIndex{2}\).
- Contestar
-
Dejar\(ε>0\); elegir\(δ=\frac{ε}{3}\); asumir\(0<|x−2|<δ\).
Por lo tanto,\(|(3x−2)−4|=|3x−6|=|3|⋅|x−2|<3⋅δ=3⋅(ε/3)=ε\).
Por lo tanto,\(\displaystyle \lim_{x→2}(3x−2)=4\).
En Ejemplos\(\PageIndex{1}\) y\(\PageIndex{2}\), las pruebas fueron bastante sencillas, ya que las funciones con las que estábamos trabajando eran lineales. En Ejemplo\(\PageIndex{3}\), vemos cómo modificar la prueba para acomodar una función no lineal.
\(\displaystyle \lim_{x→2}x^2=4\)Demuéstralo.
Solución
1. Vamos\(ε>0\). La primera parte de la definición comienza “Para cada”\(ε>0\), por lo que debemos demostrar que lo que sigue es cierto sin importar el valor positivo de que\(ε\) se elija. Al decir “Vamos”\(ε>0\), señalamos nuestra intención de hacerlo.
2. Sin pérdida de generalidad, asuma\(ε≤4\). Dos preguntas se presentan: ¿Por qué queremos\(ε≤4\) y por qué está bien hacer esta suposición? En respuesta a la primera pregunta: Más adelante, en el proceso de resolver para\(δ\), descubriremos que\(δ\) implica la cantidad\(\sqrt{4−ε}\). En consecuencia, necesitamos\(ε≤4\). En respuesta a la segunda pregunta: Si podemos encontrar\(δ>0\) que “funciona” para\(ε≤4\), entonces “funcionará” para cualquiera\(ε>4\) también. Hay que tener en cuenta que, aunque siempre está bien poner un límite superior en ε, nunca está bien poner un límite inferior (que no sea cero) encendido\(ε\).
3. Escoge\(δ=\min\{2−\sqrt{4−ε},\sqrt{4+ε}−2\}\). La figura\(\PageIndex{3}\) muestra cómo hicimos esta elección de\(δ\).
![Esta gráfica muestra cómo encontrar delta geométricamente para un épsilon dado para la prueba anterior. Primero, la función f (x) = x^2 se extrae de [-1, 3]. En el eje y, se marca el límite propuesto 4, y se dibuja la línea y=4 para intersectar con la función at (2,4). Para un épsilon dado, el punto 4 + épsilon y el 4 — épsilon están marcados en el eje y por encima y por debajo del 4. A partir de estos puntos se dibujan líneas azules para intersectar con la función, donde se dibujan líneas rosadas desde el punto de intersección hasta el eje x. Estas líneas aterrizan a ambos lados de x=2. A continuación, resolvemos para estos valores x, que aquí tienen que ser positivos. El primero es x^2 = 4 — épsilon, que simplifica a x = sqrt (4-épsilon). El siguiente es x^2 = 4 + épsilon, que simplifica a x = sqrt (4 + épsilon). Delta es la menor de las dos distancias, por lo que es el min de (2 — sqrt (4 — épsilon) y sqrt (4 + épsilon) — 2).](https://math.libretexts.org/@api/deki/files/12354/2.5.2.png)
4. Debemos mostrar: Si\(0<|x−2|<δ\), entonces\(|x^2−4|<ε\), así debemos comenzar asumiendo
\(0<|x−2|<δ.\)
Realmente no necesitamos\(0<|x−2|\) (en otras palabras,\(x≠2\)) para esta prueba. Ya que\(0<|x−2|<δ⇒|x−2|<δ\), está bien caer\(0<|x−2|\).
\(|x−2|<δ.\)
Por lo tanto,
\(−δ<x−2<δ.\)
Recordemos eso\(δ=\min\{2−\sqrt{4−ε},\sqrt{4+ε}−2\}\). Así,\(δ≥2−\sqrt{4−ε}\) y consecuentemente\(−(2−\sqrt{4−ε})≤−δ\). También utilizamos\(δ≤\sqrt{4+ε}−2\) aquí. Podríamos preguntarnos en este punto: ¿Por qué\(2−\sqrt{4−ε}\) sustituimos\(δ\) en el lado izquierdo de la desigualdad y\(\sqrt{4+ε}−2\) en el lado derecho de la desigualdad? Si nos fijamos en Figura\(\PageIndex{3}\), vemos que\(2−\sqrt{4−ε}\) corresponde a la distancia a la izquierda de\(2\) en el\(x\) eje -y\(\sqrt{4+ε}−2\) corresponde a la distancia a la derecha. Por lo tanto,
\(−(2−\sqrt{4−ε})≤−δ<x−2<δ≤\sqrt{4+ε}−2.\)
Simplificamos la expresión de la izquierda:
\(−2+\sqrt{4−ε}<x−2<\sqrt{4+ε}−2\).
Luego, agregamos 2 a todas las partes de la desigualdad:
\(\sqrt{4−ε}<x<\sqrt{4+ε}.\)
Cuadramos todas las partes de la desigualdad. Está bien hacerlo, ya que todas las partes de la desigualdad son positivas:
\(4−ε<x^2<4+ε.\)
Restamos\(4\) de todas las partes de la desigualdad:
\(−ε<x^2−4<ε.\)
Por último,
\(|x^2−4|<ε.\)
5. Por lo tanto,
\(\displaystyle \lim_{x→2}x^2=4.\)
Encuentra δ correspondiente a\(ε>0\) para una prueba de que\(\displaystyle \lim_{x→9}\sqrt{x}=3\).
- Pista
-
Dibuja una gráfica similar a la del Ejemplo\(\PageIndex{3}\).
- Contestar
-
Escoge\(δ=\text{min}\{9−(3−ε)^2,\;(3+ε)^2−9\}\).
El enfoque geométrico para demostrar que el límite de una función adquiere un valor específico funciona bastante bien para algunas funciones. Además, la penetración en la definición formal del límite que proporciona este método es invaluable. Sin embargo, también podemos acercarnos a las pruebas límite desde un punto de vista puramente algebraico. En muchos casos, un enfoque algebraico puede no solo proporcionarnos una visión adicional de la definición, sino que también puede resultar más simple. Además, un enfoque algebraico es la principal herramienta utilizada en pruebas de declaraciones sobre límites. Por ejemplo\(\PageIndex{4}\), tomamos un enfoque puramente algebraico.
Demostrar que\(\displaystyle \lim_{x→−1}\;(x^2−2x+3)=6.\)
Solución
Usemos nuestro esquema de la Estrategia de Resolución de Problemas:
1. Vamos\(ε>0\).
2. Escoge\(δ=\text{min}\{1,ε/5\}\). Esta elección de\(δ\) puede parecer extraña a primera vista, pero se obtuvo echando un vistazo a nuestra desigualdad máxima deseada:\(∣(x^2−2x+3)−6∣<ε\). Esta desigualdad equivale a\(|x+1|⋅|x−3|<ε\). En este punto, la tentación simplemente de elegir\(δ=\frac{ε}{x−3}\) es muy fuerte. Desafortunadamente, nuestra elección de\(δ\) debe depender solo de ε y de ninguna otra variable. Si podemos reemplazar\(|x−3|\) por un valor numérico, nuestro problema puede resolverse. Este es el lugar donde\(δ≤1\) entra en juego el asumir. La elección de\(δ≤1\) aquí es arbitraria. Podríamos haber usado con la misma facilidad cualquier otro número positivo. En algunas pruebas, puede ser necesario un mayor cuidado en esta elección. Ahora, desde\(δ≤1\) y\(|x+1|<δ≤1\), somos capaces de demostrar eso\(|x−3|<5\). En consecuencia,\(|x+1|⋅|x−3|<|x+1|⋅5\). En este punto nos damos cuenta de que también necesitamos\(δ≤ε/5\). Así, elegimos\(δ=\text{min}\{1,ε/5\}\).
3. Asumir\(0<|x+1|<δ\). Por lo tanto,
\[|x+1|<1\text{ and }|x+1|<\frac{ε}{5}. \nonumber \]
Ya que\(|x+1|<1\), podemos concluir que\(−1<x+1<1\). Así, restando\(4\) de todas las partes de la desigualdad, obtenemos\(−5<x−3<−1\). En consecuencia,\(|x−3|<5\). Esto nos da
\[\left|(x^2−2x+3)−6\right|=|x+1|⋅|x−3|<\frac{ε}{5}⋅5=ε.\nonumber \]
Por lo tanto,
\[\lim_{x→−1}\;(x^2−2x+3)=6.\nonumber \]
Complete la prueba de que\(\displaystyle \lim_{x→1}x^2=1\).
Dejar\(ε>0\); elegir\(δ=\text{min}\{1,ε/3\}\); asumir\(0<|x−1|<δ\).
Ya que\(|x−1|<1\), podemos concluir que\(−1<x−1<1\). Por lo tanto,\(1<x+1<3\). De ahí,\(|x+1|<3\).
- Pista
-
Use Ejemplo\(\PageIndex{4}\) como guía.
- Contestar
-
\(∣x^2−1∣=|x−1|⋅|x+1|<ε/3⋅3=ε\)
Encontrarás que, en general, cuanto más compleja sea una función, más probable es que el enfoque algebraico sea el más fácil de aplicar. El enfoque algebraico también es más útil para probar afirmaciones sobre límites.
Demostrar leyes de límite
Ahora demostramos cómo utilizar la definición épsilon-delta de un límite para construir una prueba rigurosa de una de las leyes de límite. La desigualdad triangular se utiliza en un punto clave de la prueba, por lo que primero revisamos esta propiedad clave de valor absoluto.
El triángulo de desigualdad afirma que si\(a\) y\(b\) son números reales, entonces\(|a+b|≤|a|+|b|\).
Demostramos la siguiente ley límite: Si\(\displaystyle \lim_{x→a}f(x)=L\) y\(\displaystyle \lim_{x→a}g(x)=M\), entonces\(\displaystyle \lim_{x→a}\;(f(x)+g(x))=L+M\).
Vamos\(ε>0\).
Elige\(δ_1>0\) para que si\(0<|x−a|<δ_1\), entonces\(|f(x)−L|<ε/2\).
Elige\(δ_2>0\) para que si\(0<|x−a|<δ_2\), entonces\(|g(x)−M|<ε/2\).
Escoge\(δ=\text{min}\{δ_1,δ_2\}\).
Asumir\(0<|x−a|<δ\).
Por lo tanto,
\(0<|x−a|<δ_1\)y\(0<|x−a|<δ_2\).
Por lo tanto,
\ [\ begin {align*} | (f (x) +g (x)) − (L+M) |&=| (f (x) −L) + (g (x) −M) |\\ [4pt]
&≤|f (x) −l|+|G (x) −M|\\ [4pt]
&<\ frac {ε} {2} +\ frac {ε} {2} =ε\ end {align*}. \ nonumber\]
□
Ahora exploramos lo que significa que un límite no exista. El límite\(\displaystyle \lim_{x→a}f(x)\) no existe si no hay un número real\(L\) para el cual\(\displaystyle \lim_{x→a}f(x)=L\). Así, para todos los números reales\(L\),\(\displaystyle \lim_{x→a}f(x)≠L\). Para entender lo que esto significa, miramos cada parte de la definición de\(\displaystyle \lim_{x→a}f(x)=L\) junto con su opuesto. Una traducción de la definición se da en la Tabla\(\PageIndex{2}\).
| Definición | Opuesto |
|---|---|
| 1. Para cada\(ε>0\), | 1. Existe\(ε>0\) para que |
| 2. existe una\(δ>0\), por lo que | 2. por cada\(δ>0\), |
| 3. si\(0<|x−a|<δ\), entonces\(|f(x)−L|<ε\). | 3. Hay una\(x\) satisfactoria\(0<|x−a|<δ\) para que\(|f(x)−L|≥ε\). |
Por último, podemos exponer lo que significa que un límite no exista. El límite\(\displaystyle \lim_{x→a}f(x)\) no existe si por cada número real\(L\), existe un número real para\(ε>0\) que para todos\(δ>0\), haya un\(x\) satisfactorio\(0<|x−a|<δ\), así que eso\(|f(x)−L|≥ε\). Apliquemos esto en Ejemplo\(\PageIndex{5}\) para mostrar que no existe un límite.
Demostrar que\(\displaystyle \lim_{x→0}\frac{|x|}{x}\) no existe. La gráfica de\(f(x)=|x|/x\) se muestra aquí:
0, y es una línea sin pendiente que comienza en el eje y en un círculo abierto (1,0)." src="https://math.libretexts.org/@api/dek...2355/2.5.3.png">
Solución
Supongamos que\(L\) es candidato a un límite. Escoge\(ε=1/2\).
Vamos\(δ>0\). \(L≥0\)O bien\(L<0\). Si\(L≥0\), entonces vamos\(x=−δ/2\).
Por lo tanto,
\(|x−0|=∣−\frac{δ}{2}−0∣=\frac{δ}{2}<δ\)
y
\(\left|\frac{∣−\frac{δ}{2}∣}{−\frac{δ}{2}}−L\right|=|−1−L|=L+1≥1>\frac{1}{2}=ε\).
Por otro lado, si\(L<0\), entonces vamos\(x=δ/2\). Por lo tanto,
\(|x−0|=∣\frac{δ}{2}−0∣=\frac{δ}{2}<δ\)
y
\(\left|\frac{∣\frac{δ}{2}∣}{\frac{δ}{2}}−L\right|=|1−L|=|L|+1≥1>\frac{1}{2}=ε\).
Así, por cualquier valor de\(L\),\(\displaystyle \lim_{x→0}\frac{|x|}{x}≠L.\)
Límites unilaterales
Así como primero obtuvimos una comprensión intuitiva de los límites y luego pasamos a una definición más rigurosa de un límite, ahora revisamos los límites unilaterales. Para ello, modificamos la definición épsilon-delta de un límite para dar definiciones formales épsilon-delta para límites de derecha e izquierda en un punto. Estas definiciones sólo requieren ligeras modificaciones a partir de la definición del límite. En la definición del límite desde la derecha, la desigualdad\(0<x−a<δ\) reemplaza\(0<|x−a|<δ\), lo que asegura que solo consideramos valores de\(x\) que son mayores que (a la derecha de)\(a\). De igual manera, en la definición del límite desde la izquierda, la desigualdad\(−δ<x−a<0\) reemplaza\(0<|x−a|<δ\), lo que asegura que solo consideramos valores de\(x\) que son menores que (a la izquierda de)\(a\).
Límite desde la Derecha: Dejar\(f(x)\) definirse a lo largo de un intervalo abierto de la forma\((a,b)\) donde\(a<b\). Entonces
\[\lim_{x→a^+}f(x)=L \nonumber \]
si por cada\(ε>0\), existe una\(δ>0\), tal que si\(0<x−a<δ\), entonces\(|f(x)−L|<ε\).
Límite desde la Izquierda: Dejar\(f(x)\) definirse a lo largo de un intervalo abierto de la forma\((b,c)\) donde\(b<c\). Entonces,
\[\lim_{x→c^−}f(x)=L \nonumber \]
si por cada\(ε>0\), existe\(δ>0\) tal que si\( −δ<x−c<0\), entonces\(|f(x)−L|<ε\).
Demostrar que
\[\lim_{x→4^+}\sqrt{x−4}=0.\nonumber \]
Solución
Vamos\(ε>0\).
Escoge\(δ=ε^2\). Ya que en última instancia queremos\(∣\sqrt{x−4}−0∣<ε\), manipulamos esta desigualdad para obtener\(\sqrt{x−4}<ε\) o, de manera equivalente\(0<x−4<ε^2\), hacer\(δ=ε^2\) una elección clara. También podemos determinar\(δ\) geométricamente, como se muestra en la Figura\(\PageIndex{4}\).
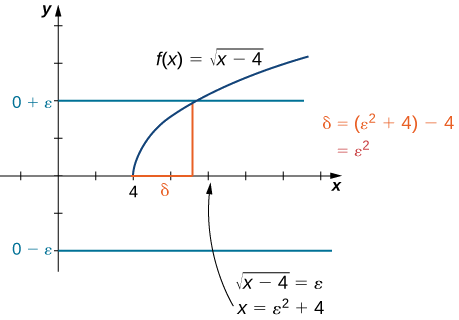
Asumir\(0<x−4<δ\). Por lo tanto,\(0<x−4<ε^2\). De ahí,\(0<\sqrt{x−4}<ε\). Por último,\(\left|\sqrt{x−4}−0\right|<ε\). Por lo tanto,\(\displaystyle \lim_{x→4^+}\sqrt{x−4}=0\).
Encontrar\(δ\) correspondiente a\(ε\) para una prueba de que\(\displaystyle \lim_{x→1^−}\sqrt{1−x}=0\).
- Pista
-
Dibuja la gráfica y usa Ejemplo\(\PageIndex{6}\) como guía de resolución.
- Contestar
-
\(δ=ε^2\)
Límites Infinitos
Concluimos el proceso de convertir nuestras ideas intuitivas de diversos tipos de límites a definiciones formales rigurosas, persiguiendo una definición formal de límites infinitos. Para tener\(\displaystyle \lim_{x→a}f(x)=+∞\), queremos que los valores de la función se hagan cada\(f(x)\) vez más grandes a medida que se\(x\) aproxima\(a\). En lugar del requisito de que\(|f(x)−L|<ε\) para arbitrariamente pequeño\(ε\) cuando\(0<|x−a|<δ\) para lo suficientemente pequeño\(δ\), queremos\(f(x)>M\) para arbitrariamente grande positivo\(M\) cuando\(0<|x−a|<δ\) para lo suficientemente pequeño\(δ\). La figura\(\PageIndex{5}\) ilustra esta idea mostrando el valor de\(δ\) para valores sucesivamente mayores de\(M\).
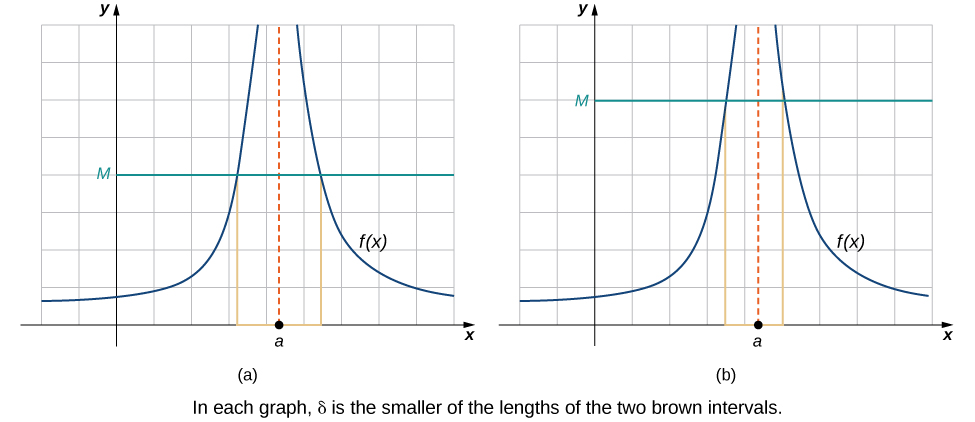
Figura\(\PageIndex{5}\): Estas gráficas representan valores de\(δ\) para\(M\) para mostrar eso\(\displaystyle \lim_{x→a}f(x)=+∞\).
Let\(f(x)\) be defined for all \(x≠a\) in an open interval containing \(a\). Then, we have an infinite limit
\[\lim_{x→a}f(x)=+∞ \nonumber \]
si por cada\(M>0\), there exists \(δ>0\) such that if \(0<|x−a|<δ\), then \(f(x)>M\).
Let\(f(x)\) be defined for all \(x≠a\) in an open interval containing \(a\). Then, we have a negative infinite limit
\[\lim_{x→a}f(x)=−∞ \nonumber \]
si por cada\(M>0\), there exists \(δ>0\) such that if \(0<|x−a|<δ\), then \(f(x)<−M\).
Demostrar que\(\displaystyle \lim_{x→3}\frac{1}{(x-3)^2}=\infty.\)
Solución
Utilizamos un enfoque muy similar a nuestra anterior Estrategia de Resolución de Problemas. Primero encontramos un apropiado\(δ>0\). Entonces escribimos nuestra prueba.
Paso 1: Primero encontramos un apropiado\(δ>0\).
1. \(M\)Sea cualquier número real tal que\(M>0\).
2. Vamos\(f(x) = \dfrac{1}{(x-3)^2} > M\). Entonces resolvemos para la expresión\(x - 3\).
Multiplicar ambos lados de la desigualdad por la cantidad positiva\((x - 3)^2\) y dividir ambos lados por la cantidad positiva nos\(M\) da:
\[ \frac{1}{M} > (x-3)^2 \nonumber \]
Tomando la raíz cuadrada de ambos lados, tenemos,
\[ \sqrt{\frac{1}{M}} > |x - 3|. \qquad \quad\left(\text{Remember that }\sqrt{x^2} = |x|.\right)\nonumber \]
Reescribir esta declaración nos da,\(0 < |x-3| < \sqrt{\dfrac{1}{M}}\). De esto elegimos\(δ = \sqrt{\dfrac{1}{M}}\).
Paso 2: Ahora escribimos una prueba.
3. Dejemos\(δ = \sqrt{\dfrac{1}{M}}\) y asuma\(0 < |x-3| < δ = \sqrt{\dfrac{1}{M}}\).
Por lo tanto,
\[ |x-3| < \sqrt{\frac{1}{M}}. \nonumber \]
Al cuadrar ambos lados nos da,
\[ (x-3)^2 < \frac{1}{M}. \nonumber \]
Tomando el recíproco de ambas partes (y recordando que esto invertirá la dirección de la desigualdad),
\[ \dfrac{1}{(x-3)^2} > M. \nonumber \]
Por lo tanto, hemos demostrado que
\[\lim_{x→3}\frac{1}{(x-3)^2}=\infty.\nonumber \]
Se necesitará una prueba muy similar para un límite que sea igual a\(-\infty\).
Tenga en cuenta que a menudo será necesario tomar un enfoque de límite unilateral con este tipo de límite. Por ejemplo, para probar:\(\displaystyle \lim_{x\to 0^+}\frac{1}{x} = \infty\).
Conceptos clave
- La noción intuitiva de un límite puede convertirse en una definición matemática rigurosa conocida como la definición épsilon-delta del límite.
- La definición épsilon-delta puede ser utilizada para probar declaraciones sobre límites.
- La definición épsilon-delta de un límite puede modificarse para definir límites unilaterales.
- Una definición similar de un límite infinito se puede utilizar para probar declaraciones sobre límites infinitos.
Glosario
- épsilon-delta definición del límite
- \(\displaystyle \lim_{x→a}f(x)=L\)si por cada\(ε>0\), existe\(δ>0\) tal que si\(0<|x−a|<δ\), entonces\(|f(x)−L|<ε\)
- desigualdad triangular
- Si\(a\) y\(b\) son números reales, entonces\(|a+b|≤|a|+|b|\)
- definición formal de un límite infinito
- \(\displaystyle \lim_{x→a}f(x)=\infty\)si por cada\(M>0\), existe\(δ>0\) tal que si\(0<|x−a|<δ\), entonces\(f(x)>M\)
\(\displaystyle \lim_{x→a}f(x)=-\infty\) si por cada\(M>0\), existe\(δ>0\) tal que si\(0<|x−a|<δ\), entonces\(f(x)<-M\)
Colaboradores y Atribuciones
- Template:ContribOpenStaxCalc
- Paul Seeburger (Monroe Community College), added Example \(\PageIndex{7}\) and entries for infinite limits under Key Concepts and the Glossary.


