5.5E: Ejercicios para la Sección 5.5

1) ¿Por qué\(u\) -sustitución se refiere como un cambio de variable?

2) Si\( f=g∘h\), al invertir la regla de la cadena\(\dfrac{d}{dx}(g∘h)(x)=g′(h(x))h′(x)\),, debe tomar\( u=g(x)\) o\(u=h(x)?\)

Contestar

\(u=h(x)\)

En los ejercicios 3 a 7, verificar cada identidad utilizando la diferenciación. Luego, utilizando la\(u\) sustitución indicada, identificar de\(f\) tal manera que la integral tome la forma\(\displaystyle∫f(u)\,du.\)

3)\(\displaystyle ∫x\sqrt{x+1}\,dx=\frac{2}{15}(x+1)^{3/2}(3x−2)+C;\quad u=x+1\)

4)\(\displaystyle∫\frac{x^2}{\sqrt{x−1}}\,dx=\frac{2}{15}\sqrt{x−1}(3x^2+4x+8)+C,\quad (x>1);\quad u=x−1\)

Contestar

\( f(u)=\dfrac{(u+1)^2}{\sqrt{u}}\)

5)\(\displaystyle∫x\sqrt{4x^2+9}\,dx=\frac{1}{12}(4x^2+9)^{3/2}+C;\quad u=4x^2+9\)

6)\(\displaystyle∫\frac{x}{\sqrt{4x^2+9}}\,dx=\frac{1}{4}\sqrt{4x^2+9}+C;\quad u=4x^2+9\)

Contestar

\( du=8x\,dx;\quad f(u)=\frac{1}{8\sqrt{u}}\)

7)\(\displaystyle∫\frac{x}{(4x^2+9)^2}\,dx=−\frac{1}{8(4x^2+9)} + C;\quad u=4x^2+9\)

En los ejercicios 8 - 17, encuentra la antiderivada utilizando la sustitución indicada.

8)\(\displaystyle∫(x+1)^4\,dx;\quad u=x+1\)

Contestar

\(\displaystyle∫(x+1)^4\,dx = \frac{1}{5}(x+1)^5+C\)

9)\(\displaystyle∫(x−1)^5\,dx;\quad u=x−1\)

10)\(\displaystyle∫(2x−3)^{−7}\,dx;\quad u=2x−3\)

Contestar

\(\displaystyle∫(2x−3)^{−7}\,dx = −\frac{1}{12(2x−3)^6}+C\)

11)\(\displaystyle∫(3x−2)^{−11}\,dx;\quad u=3x−2\)

12)\(\displaystyle∫\frac{x}{\sqrt{x^2+1}}\,dx;\quad u=x^2+1\)

Contestar

\(\displaystyle∫\frac{x}{\sqrt{x^2+1}}\,dx = \sqrt{x^2+1}+C\)

13)\(\displaystyle∫\frac{x}{\sqrt{1−x^2}}\,dx;\quad u=1−x^2\)

14)\(\displaystyle∫(x−1)(x^2−2x)^3\,dx;\quad u=x^2−2x\)

Contestar

\(\displaystyle∫(x−1)(x^2−2x)^3\,dx = \frac{1}{8}(x^2−2x)^4+C\)

15)\(\displaystyle∫(x^2−2x)(x^3−3x^2)^2\,dx;\quad u=x^3=3x^2\)

16)\(\displaystyle∫\cos^3 θ\,dθ;\quad u=\sin θ\) (Pista:\(\cos^2 θ=1−\sin^2 θ\))

Contestar

\(\displaystyle∫\cos^3 θ\,dθ = \sin θ−\dfrac{\sin^3 θ}{3}+C\)

17)\(\displaystyle ∫\sin^3 θ\,dθ;\quad u=\cos θ\) (Pista:\(\sin^2 θ=1−\cos^2θ\))

En los ejercicios 18 - 34, utilizar un cambio adecuado de variables para determinar la integral indefinida.

18)\(\displaystyle∫x(1−x)^{99}\,dx\)

Contestar

\ (\ begin {alinear*}\ displaystylex (1−x) ^ {99}\, dx &=\ frac {(1−x) ^ {101}} {101} −\ frac {(1−x) ^ {100}} {100} +C\\ [4pt]
&=-\ frac {(1-x) ^ {100}} {10100}\ grande [100x + 1\ grande] +C\ final {alinear*}\)

19)\(\displaystyle∫t(1−t^2)^{10}dt\)

20)\(\displaystyle∫(11x−7)^{−3}\,dx\)

Contestar

\(\displaystyle∫(11x−7)^{−3}\,dx = −\frac{1}{22(11x−7)^2}+C\)

21)\(\displaystyle∫(7x−11)^4\,dx\)

22)\(\displaystyle∫\cos^3 θ\sin θ\,dθ\)

Contestar

\(\displaystyle∫\cos^3 θ\sin θ\,dθ = −\frac{\cos^4 θ}{4}+C\)

23)\(\displaystyle∫\sin^7 θ\cos θ\,dθ\)

24)\(\displaystyle∫\cos^2(πt)\sin(πt)\,dt\)

Contestar

\(\displaystyle∫\cos^2(πt)\sin(πt)\,dt = −\frac{cos^3(πt)}{3π}+C\)

25)\(\displaystyle∫\sin^2 x\cos^3 x\,dx\) (Pista:\(\sin^2 x+\cos^2 x=1\))

26)\(\displaystyle∫t\sin(t^2)\cos(t^2)\,dt\)

Contestar

\(\displaystyle∫t\sin(t^2)\cos(t^2)\,dt = −\frac{1}{4}\cos^2(t^2)+C\)

27)\(\displaystyle∫t^2\cos^2(t^3)\sin(t^3)\,dt\)

28)\(\displaystyle∫\frac{x^2}{(x^3−3)^2}\,dx\)

Contestar

\(\displaystyle∫\frac{x^2}{(x^3−3)^2}\,dx = −\frac{1}{3(x^3−3)}+C\)

29)\(\displaystyle∫\frac{x^3}{\sqrt{1−x^2}}\,dx\)

30)\(\displaystyle∫\frac{y^5}{(1−y^3)^{3/2}}\,dy\)

Contestar

\(\displaystyle∫\frac{y^5}{(1−y^3)^{3/2}}\,dy = −\frac{2(y^3−2)}{3\sqrt{1−y^3}}+C\)

31)\(\displaystyle∫\cos θ(1−\cos θ)^{99}\sin θ\,dθ\)

32)\(\displaystyle∫(1−\cos^3 θ)^{10}\cos^2 θ\sin θ\,dθ\)

Contestar

\(\displaystyle∫(1−\cos^3 θ)^{10}\cos^2 θ\sin θ\,dθ = \frac{1}{33}(1−\cos^3 θ)^{11}+C\)

33)\(\displaystyle∫(\cos θ−1)(\cos^2 θ−2\cos θ)^3\sin θ\,dθ\)

34)\(\displaystyle∫(\sin^2 θ−2\sin θ)(\sin^3 θ−3\sin^2 θ)^3\cos θ\,dθ\)

Contestar

\(\displaystyle∫(\sin^2 θ−2\sin θ)(\sin^3 θ−3\sin^2 θ)^3\cos θ\,dθ = \frac{1}{12}(\sin^3 θ−3\sin^2 θ)^4+C\)

En los ejercicios 35 - 38, usa una calculadora para estimar el área bajo la curva usando sumas de Riemann izquierda con 50 términos, luego usa la sustitución para resolver la respuesta exacta.

35) [T]\(y=3(1−x)^2\) sobre\([0,2]\)

36) [T]\(y=x(1−x^2)^3\) sobre\([−1,2]\)

Contestar

\(L_{50}=−8.5779.\)El área exacta es\(\frac{−81}{8}\) unidades\(^2\).

37) [T]\(y=\sin x(1−\cos x)^2\) sobre\([0,π]\)

38) [T]\(y=\dfrac{x}{(x^2+1)^2}\) sobre\([−1,1]\)

Contestar

\(L_{50}=−0.006399\). El área exacta es 0.

En los ejercicios 39 - 44, utilizar un cambio de variables para evaluar la integral definida.

39)\(\displaystyle∫^1_0x\sqrt{1−x^2}\,dx\)

40)\(\displaystyle∫^1_0\frac{x}{\sqrt{1+x^2}}\,dx\)

Contestar

\(\displaystyle u=1+x^2,\quad du=2x\,dx,\quad ∫^1_0\frac{x}{\sqrt{1+x^2}}\,dx = \frac{1}{2}∫^2_1u^{−1/2}du=\sqrt{2}−1\)

41)\(\displaystyle∫^2_0\frac{t}{\sqrt{5+t^2}}\,dt\)

42)\(\displaystyle∫^1_0\frac{t^2}{\sqrt{1+t^3}}\,dt\)

Contestar

\(\displaystyle u=1+t^3,\quad du=3t^2,\quad ∫^1_0\frac{t^2}{\sqrt{1+t^3}}\,dt = \frac{1}{3}∫^2_1u^{−1/2}du=\frac{2}{3}(\sqrt{2}−1)\)

43)\(\displaystyle∫^{π/4}_0\sec^2 θ\tan θ\,dθ\)

44)\(\displaystyle∫^{π/4}_0\frac{\sin θ}{\cos^4 θ}\,dθ\)

Contestar

\(\displaystyle u=\cos θ,\quad du=−\sin θ\,dθ,\quad \int^{π/4}_0\frac{\sin θ}{\cos^4 θ}\,dθ = -∫_1^{\sqrt{2}/2}u^{−4}\,du = ∫^1_{\sqrt{2}/2}u^{−4}\,du=\frac{1}{3}(2\sqrt{2}−1)\)

En los ejercicios 45 - 50, evaluar la integral indefinida\(\displaystyle ∫f(x)\,dx\) con constante\(C=0\) usando\(u\) -sustitución. Después, grafica la función y la antiderivada sobre el intervalo indicado. De ser posible, estimar un valor de\(C\) ese habría que sumar a la antiderivada para que sea igual a la integral definida\(\displaystyle F(x)=∫^x_af(t)\,dt\), con un punto final izquierdo del intervalo dado.

45) [T]\(\displaystyle∫(2x+1)e^{x^2+x−6}\,dx\) sobre\([−3,2]\)

46) [T]\(\displaystyle∫\frac{\cos(\ln(2x))}{x}\,dx\) en\([0,2]\)

Contestar

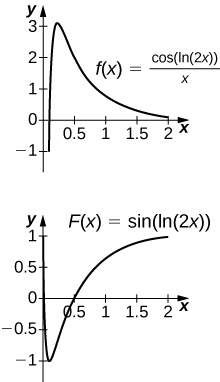
El antiderivado es\(y=\sin(\ln(2x))\). Dado que el antiderivado no es continuo en\(x=0\), no se puede encontrar un valor de C que haga\(y=\sin(\ln(2x))−C\) funcionar como una integral definida.

47) [T]\(\displaystyle ∫\frac{3x^2+2x+1}{\sqrt{x^3+x^2+x+4}}\,dx\) sobre\([−1,2]\)

48) [T]\(\displaystyle ∫\frac{\sin x}{\cos^3x}\,dx\) sobre\(\left[−\frac{π}{3},\frac{π}{3}\right]\)

Contestar

El antiderivado es\(y=\frac{1}{2}\sec^2 x\). Deberías tomar\(C=−2\) para que\(F(−\frac{π}{3})=0.\)

49) [T]\(\displaystyle ∫(x+2)e^{−x^2−4x+3}\,dx\) sobre\([−5,1]\)

50) [T]\(\displaystyle ∫3x^2\sqrt{2x^3+1}\,dx\) sobre\([0,1]\)

Contestar

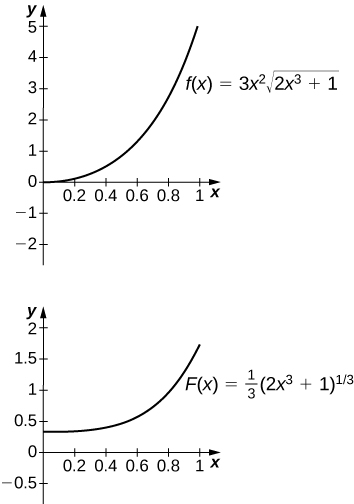
El antiderivado es\( y=\frac{1}{3}(2x^3+1)^{3/2}\). Uno debe tomar\(C=−\frac{1}{3}\).

51) Si\(h(a)=h(b)\) en\(\displaystyle ∫^b_ag'(h(x))h(x)\,dx,\) qué se puede decir sobre el valor de la integral?

52) ¿Está\(\displaystyle ∫^2_0\frac{x}{1−x^2}\,dx\) bien la sustitución\(u=1−x^2\) en la integral definitiva? Si no, ¿por qué no?

Contestar

No, porque el integrando es discontinuo en\(x=1\).

En los ejercicios 53 - 59, utilizar un cambio de variables para mostrar que cada integral definida es igual a cero.

53)\(\displaystyle ∫^π_0\cos^2(2θ)\sin(2θ)\,dθ\)

54)\(\displaystyle ∫^\sqrt{π}_0t\cos(t^2)\sin(t^2)\,dt\)

Contestar

\(u=\sin(t^2);\)la integral se convierte\(\displaystyle \frac{1}{2}∫^0_0u\,du.\)

55)\(\displaystyle ∫^1_0(1−2t)\,dt\)

56)\(\displaystyle ∫^1_0\frac{1−2t}{1+(t−\frac{1}{2})^2}\,dt\)

Contestar

\(u=1+(t−\frac{1}{2})^2;\)la integral se convierte\(\displaystyle −∫^{5/4}_{5/4}\frac{1}{u}\,du\).

57)\(\displaystyle ∫^π_0\sin\left(\left(t−\tfrac{π}{2}\right)^3\right)\cos\left(t−\tfrac{π}{2}\right)\,dt\)

58)\(\displaystyle ∫^2_0(1−t)\cos(πt)\,dt\)

Contestar

\(u=1−t;\)Dado que el integrando es extraño, la integral se convierte
\[∫^{−1}_1u\cos\big(π(1−u)\big)\,du=∫^{−1}_1u[\cos π\cos u−\sin π\sin u]\,du=−∫^{−1}_1u\cos u\,du=∫_{-1}^1u\cos u\,du=0\nonumber \]

59)\(\displaystyle ∫^{3π/4}_{π/4}\sin^2 t\cos t\,dt\)

60) Mostrar que el valor promedio de\(f(x)\) más de un intervalo\([a,b]\) es el mismo que el valor promedio de\(f(cx)\) sobre el intervalo\(\left[\frac{a}{c},\frac{b}{c}\right]\) para\(c>0.\)

Contestar

Configuración\(u=cx\) y te\(du=c\,dx\) pone\(\displaystyle \frac{1}{\frac{b}{c}−\frac{a}{c}}∫^{b/c}_{a/c}f(cx)\,dx=\frac{c}{b−a}∫^{u=b}_{u=a}f(u)\frac{du}{c}=\frac{1}{b−a}∫^b_af(u)\,du.\)

61) Encontrar el área bajo la gráfica de\(f(t)=\dfrac{t}{(1+t^2)^a}\) entre\(t=0\) y\(t=x\) dónde\(a>0\) y\(a≠1\) es fija, y evaluar el límite como\(x→∞\).

62) Encuentra el área bajo la gráfica de\(g(t)=\dfrac{t}{(1−t^2)^a}\) entre\(t=0\) y\(t=x\), donde\(0<x<1\) y\(a>0\) es fija. Evaluar el límite como\(x→1\).

Contestar

\(\displaystyle ∫^x_0g(t)\,dt=\frac{1}{2}∫^1_{u=1−x^2} \frac{du}{u^a}=\frac{1}{2(1−a)}u^{1−a}∣1u=\frac{1}{2(1−a)}(1−(1−x^2)^{1−a})\)Como\(x→1\) el límite es\(\dfrac{1}{2(1−a)}\) si\(a<1\), y el límite diverge a\(+∞\) si\(a>1\).

63) El área de un semicírculo de radio se\(1\) puede expresar como\(\displaystyle ∫^1_{−1}\sqrt{1−x^2}\,dx\). Utilice la sustitución\(x=\cos t\) para expresar el área de un semicírculo como la integral de una función trigonométrica. No es necesario computar la integral.

64) El área de la mitad superior de una elipse con un eje mayor que es el\(x\) -eje de\(x=−1\) a y con un eje menor que es el\(y\) -eje de\(y=−b\) a se\(y=b\) puede escribir como\(\displaystyle ∫^a_{−a}b\sqrt{1−\frac{x^2}{a^2}}\,dx\). Utilizar la sustitución\(x=a\cos t\) para expresar esta área en términos de una integral de una función trigonométrica. No es necesario computar la integral.

Contestar

\(\displaystyle ∫^{t=0}_{t=π}b\sqrt{1−\cos^2 t}×(−a\sin t)\,dt=∫^{t=π}_{t=0}ab\sin^2 t\,dt\)

65) [T] La siguiente gráfica es de una función de la forma\( f(t)=a\sin(nt)+b\sin(mt)\). Estimar los coeficientes\(a\) y\(b\) y los parámetros de frecuencia\(n\) y\(m\). Utilice estas estimaciones para aproximarse\(\displaystyle ∫^π_0f(t)\,dt\).

66) [T] La siguiente gráfica es de una función de la forma\(f(x)=a\cos(nt)+b\cos(mt)\). Estimar los coeficientes\(a\) y\(b\) y los parámetros de frecuencia\(n\) y\(m\). Utilice estas estimaciones para aproximar\(\displaystyle ∫^π_0f(t)\,dt.\)

Contestar

\(f(t)=2\cos(3t)−\cos(2t);\quad \displaystyle ∫^{π/2}_0(2\cos(3t)−\cos(2t))\,dt=−\frac{2}{3}\)