5.6: Integrales que involucran funciones exponenciales y logarítmicas
- Page ID
- 116212
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Integrar funciones que involucran funciones exponenciales.
- Integrar funciones que involucran funciones logarítmicas.
Las funciones exponenciales y logarítmicas se utilizan para modelar el crecimiento de la población, el crecimiento celular y el crecimiento financiero, así como la depreciación, la desintegración radiactiva y el consumo de recursos, por nombrar solo algunas aplicaciones. En esta sección, exploramos la integración que involucra funciones exponenciales y logarítmicas.
Integrales de funciones exponenciales
La función exponencial es quizás la función más eficiente en términos de las operaciones de cálculo. La función exponencial,\(y=e^x\), es su propia derivada y su propia integral.
Las funciones exponenciales se pueden integrar usando las siguientes fórmulas.
\[ \begin{align} ∫e^x\,dx &= e^x+C \\[4pt] ∫a^x\,dx &=\dfrac{a^x}{\ln a}+C \end{align} \nonumber \]
Encuentra la antiderivada de la función exponencial\(e^{−x}\).
Solución
Use sustitución, ajuste\(u=−x,\) y luego\(du=−1\,dx\). Multiplica la\(du\) ecuación por\(−1\), así que ahora tienes\(−du=\,dx\). Entonces,
\[∫e^{−x}\,dx=−∫e^u\,du=−e^u+C=−e^{−x}+C. \nonumber \]
Encuentra la antiderivada de la función usando la sustitución:\(x^2e^{−2x^3}\).
- Pista
-
Vamos\(u\) a igualar el exponente en\(e\).
- Contestar
-
\(\displaystyle ∫x^2e^{−2x^3}\,dx=−\dfrac{1}{6}e^{−2x^3}+C\)
Un error común al tratar con expresiones exponenciales es tratar al exponente de\(e\) la misma manera que tratamos a los exponentes en expresiones polinómicas. No podemos usar la regla de poder para el exponente encendido\(e\). Esto puede resultar especialmente confuso cuando tenemos tanto exponenciales como polinomios en la misma expresión, como en el punto de control anterior. En estos casos, siempre debemos volver a verificar para asegurarnos de que estamos usando las reglas adecuadas para las funciones que estamos integrando.
Encuentra la antiderivada de la función exponencial\(e^x\sqrt{1+e^x}\).
Solución
Primero reescribe el problema usando un exponente racional:
\[∫e^x\sqrt{1+e^x}\,dx=∫e^x(1+e^x)^{1/2}\,dx.\nonumber \]
Usando la sustitución, elija\(u=1+e^x\). Entonces,\(du=e^x\,dx\). Tenemos
\[∫e^x(1+e^x)^{1/2}\,dx=∫u^{1/2}\,du.\nonumber \]
Entonces
\[∫u^{1/2}\,du=\dfrac{u^{3/2}}{3/2}+C=\dfrac{2}{3}u^{3/2}+C=\dfrac{2}{3}(1+e^x)^{3/2}+C\nonumber \]
![Una gráfica de la función f (x) = e^x * sqrt (1 + e^x), que es una curva ascendente cóncava creciente, sobre [-3, 1]. Comienza cerca del eje x en el cuadrante dos, cruza el eje y en (0, sqrt (2)), y continúa aumentando rápidamente.](https://math.libretexts.org/@api/deki/files/12432/5.6.1.png)
Encuentra el antiderivado de\(e^x(3e^x−2)^2\).
- Pista
-
Vamos\(u=3e^x−2\).
- Contestar
-
\(\displaystyle ∫e^x(3e^x−2)^2\,dx=\dfrac{1}{9}(3e^x−2)^3+C\)
Utilizar la sustitución para evaluar la integral indefinida\(\displaystyle ∫3x^2e^{2x^3}\,dx.\)
Solución
Aquí elegimos dejar\(u\) igualar la expresión en el exponente sobre\(e\). Dejar\(u=2x^3\) y\(du=6x^2\,dx\). Nuevamente,\(du\) está apagado por un multiplicador constante; la función original contiene un factor de\(3x^2,\) no\(6x^2\). Multiplique ambos lados de la ecuación por\(\dfrac{1}{2}\) para que el integrando en\(u\) sea igual al integrando en\(x\). Así,
\[∫3x^2e^{2x^3}\,dx=\frac{1}{2}∫e^u\,du. \nonumber \]
Integrar la expresión en\(u\) y luego sustituir la expresión original de\(x\) nuevo en la\(u\) -integral:
\[\frac{1}{2}∫e^u\,du=\frac{1}{2}e^u+C=\frac{1}{2}e^2x^3+C. \nonumber \]
Evaluar la integral indefinida\(\displaystyle ∫2x^3e^{x^4}\,dx\).
- Pista
-
Let\(u=x^4.\)
- Contestar
-
\(\displaystyle ∫2x^3e^{x^4}\,dx=\frac{1}{2}e^{x^4}+C\)
Como se mencionó al inicio de esta sección, las funciones exponenciales se utilizan en muchas aplicaciones de la vida real. El número\(e\) suele estar asociado con un crecimiento compuesto o acelerado, como hemos visto en secciones anteriores sobre la derivada. Aunque la derivada representa una tasa de cambio o una tasa de crecimiento, la integral representa el cambio total o el crecimiento total. Veamos un ejemplo en el que la integración de una función exponencial resuelve una aplicación comercial común.
Una función precio-demanda nos dice la relación entre la cantidad de un producto demandado y el precio del producto. En general, el precio disminuye a medida que aumenta la cantidad demandada. La función precio-demanda marginal es la derivada de la función precio-demanda y nos dice qué tan rápido cambia el precio en un determinado nivel de producción. Estas funciones se utilizan en los negocios para determinar el precio-elasticidad de la demanda, y para ayudar a las empresas a determinar si cambiar los niveles de producción sería rentable.
Encuentre la ecuación precio-demanda para una marca particular de pasta de dientes en una cadena de supermercados cuando la demanda es de\(50\) tubos por semana a $2.35 por tubo, dado que la función de precio-demanda marginal,\(p′(x),\) para el\(x\) número de tubos por semana, se da como
\[p'(x)=−0.015e^{−0.01x}. \nonumber \]
Si la cadena de supermercados vende\(100\) tubos por semana, ¿qué precio debería fijar?
Solución
Para encontrar la ecuación precio-demanda, integre la función precio-demanda marginal. Primero encuentra el antiderivado, luego mira los datos. Así,
\[p(x)=∫−0.015e^{−0.01x}\,dx=−0.015∫e^{−0.01x}\,dx. \nonumber \]
Usando sustitución, let\(u=−0.01x\) y\(du=−0.01\,dx\). Entonces, divide ambos lados de la\(du\) ecuación por\(−0.01\). Esto da
\[\dfrac{−0.015}{−0.01}∫e^u\,du=1.5∫e^u\,du=1.5e^u+C=1.5e^{−0.01}x+C. \nonumber \]
El siguiente paso es resolver para\(C\). Sabemos que cuando el precio es de $2.35 por tubo, la demanda es de\(50\) tubos por semana. Esto significa
\[p(50)=1.5e^{−0.01(50)}+C=2.35. \nonumber \]
Ahora, solo resuelva para\(C\):
\[C=2.35−1.5e^{−0.5}=2.35−0.91=1.44. \nonumber \]
Así,
\[p(x)=1.5e^{−0.01x}+1.44. \nonumber \]
Si el supermercado vende\(100\) tubos de pasta de dientes por semana, el precio sería
\[p(100)=1.5e−0.01(100)+1.44=1.5e−1+1.44≈1.99. \nonumber \]
El supermercado debe cobrar $1.99 por tubo si está vendiendo\(100\) tubos por semana.
Evaluar la integral definida\(\displaystyle ∫^2_1e^{1−x}\,dx.\)
Solución
Nuevamente, la sustitución es el método a utilizar. Que\(u=1−x,\) así\(\,du=−1\,dx\) o\(−\,du=\,dx\). Entonces\(\displaystyle ∫e^{1−x}\,dx=−∫e^u\,du.\)
A continuación, cambiar los límites de la integración. Usando la ecuación\(u=1−x\), tenemos:
\[\text{When }x = 1, \quad u=1−(1)=0, \nonumber \]
\[\text{and when }x = 2, \quad u=1−(2)=−1. \nonumber \]
La integral se convierte entonces
\[\begin{align*} ∫^2_1e^{1−x}\,\,dx &= −∫^{−1}_0e^u\,\,du \\[4pt] &=∫^0_{−1}e^u\,\,du \\[4pt] &=e^u\bigg|^0_{−1}=e^0−(e^{−1}) \\[4pt] &=−e^{−1}+1. \end{align*}\]
Ver Figura\(\PageIndex{2}\).
![Una gráfica de la función f (x) = e^ (1-x) sobre [0, 3]. Cruza el eje y en (0, e) como una curva ascendente cóncava decreciente y se acerca sintométicamente a 0 a medida que x va al infinito.](https://math.libretexts.org/@api/deki/files/12433/5.6.2.png)
Evaluar\(\displaystyle ∫^2_0e^{2x}\,dx.\)
- Pista
-
Let\(u=2x.\)
- Contestar
-
\(\displaystyle \frac{1}{2}∫^4_0e^u\,du=\dfrac{1}{2}(e^4−1)\)
Supongamos que la tasa de crecimiento de bacterias en una placa de Petri viene dada por\(q(t)=3^t\), donde\(t\) se da en horas y\(q(t)\) se da en miles de bacterias por hora. Si un cultivo comienza con\(10,000\) bacterias, encuentra una función\(Q(t)\) que dé el número de bacterias en la placa de Petri en cualquier momento\(t\). ¿Cuántas bacterias hay en el plato después de\(2\) horas?
Solución
Tenemos
\[Q(t)=∫3^tdt=\dfrac{3^t}{\ln 3}+C. \nonumber \]
Entonces, en\(Q(0)=10=\dfrac{1}{\ln 3}+C,\) lo\(t=0\) tenemos\(C≈9.090\) y conseguimos
\[Q(t)=\dfrac{3^t}{\ln 3}+9.090. \nonumber \]
En el momento\(t=2\), tenemos
\[\begin{align*} Q(2) &=\dfrac{3^2}{\ln 3}+9.090 \\[4pt] &\approx 17.282. \end{align*}\]
Después de 2 horas, hay 17.282 bacterias en el platillo.
De Ejemplo, supongamos que las bacterias crecen a un ritmo de\(q(t)=2^t\). Supongamos que el cultivo aún comienza con\(10,000\) bacterias. Encuentra\(Q(t)\). ¿Cuántas bacterias hay en el plato después de\(3\) horas?
- Pista
-
Utilice el procedimiento de Ejemplo\(\PageIndex{6}\) para resolver el problema
- Contestar
-
\[\begin{align*} Q(t) &= \dfrac{2^t}{\ln 2} + 8.557. \\[4pt] Q(3) &\approx 20,099 \end{align*}\]
Por lo que hay\(20,099\) bacterias en el plato después de\(3\) horas.
Supongamos que una población de moscas de la fruta aumenta a un ritmo de\(g(t)=2e^{0.02t}\), en moscas por día. Si la población inicial de moscas de la fruta son\(100\) moscas, ¿cuántas moscas hay en la población después de\(10\) días?
Solución
Dejar\(G(t)\) representar el número de moscas en la población en el momento\(t\). Aplicando el teorema del cambio neto, tenemos
\[ \begin{align*} G(10)=G(0)+∫^{10}_02e^{0.02t}\,dt \\[4pt] &=100+\left[\dfrac{2}{0.02}e^{0.02t}\right]∣^{10}_0 \\[4pt] &=100+\left[100e^{0.02t}\right]∣^{10}_0 \\[4pt] &=100+100e^{0.2}−100 \\[4pt] &≈122. \end{align*}\]
Hay\(122\) moscas en la población después de\(10\) días.
Supongamos que la tasa de crecimiento de la población de moscas viene dada por\(g(t)=e^{0.01t},\) y la población inicial de\(100\) moscas es moscas. ¿Cuántas moscas hay en la población después de\(15\) días?
- Pista
-
Utilice el proceso de Ejemplo\(\PageIndex{7}\) para resolver el problema.
- Contestar
-
Hay\(116\) moscas.
Evaluar la integral definida mediante sustitución:\[∫^2_1\dfrac{e^{1/x}}{x^2}\,dx.\nonumber \]
Solución
Este problema requiere algo de reescritura para simplificar la aplicación de las propiedades. Primero, reescribe el exponente en e como una potencia de\(x\), luego lleva el\(x^2\) en el denominador hasta el numerador usando un exponente negativo. Tenemos
\[∫^2_1\dfrac{e^{1/x}}{x^2}\,\,dx=∫^2_1e^{x^{−1}}x^{−2}\,dx. \nonumber \]
Deja que\(u=x^{−1},\) el exponente se ponga en marcha\(e\). Entonces
\[du=−x^{−2}\,dx \nonumber \]
\[−du=x^{−2}\,dx. \nonumber \]
Llevando el signo negativo fuera del signo integral, el problema ahora dice
\[−∫e^u\,du. \nonumber \]
A continuación, cambie los límites de la integración:
\[u=(1)^{−1}=1 \nonumber \]
\[u=(2)^{−1}=\dfrac{1}{2}. \nonumber \]
Observe que ahora los límites comienzan con el número mayor, lo que significa que podemos multiplicar por\(−1\) e intercambiar los límites. Así,
\[−∫^{1/2}_1e^u\,du=∫^1_{1/2}e^u\,du=e^u\big|^1_{1/2}=e−e^{1/2}=e−\sqrt{e}.\nonumber \]
Evaluar la integral definida mediante sustitución:\[∫^2_1\dfrac{1}{x^3}e^{4x^{−2}}\,dx.\nonumber \]
- Pista
-
Let\(u=4x^{−2}.\)
- Contestar
-
\(\displaystyle ∫^2_1\dfrac{1}{x^3}e^{4x^{−2}}\,dx=\dfrac{1}{8}[e^4−e]\).
Integrales que involucran funciones logarítmicas
Integrar funciones del formulario\(f(x)=x^{−1}\) dan como resultado el valor absoluto de la función logarítmica natural, como se muestra en la siguiente regla. Las fórmulas integrales para otras funciones logarítmicas, como\(f(x)=\ln x\) y\(f(x)=\log_a x\), también se incluyen en la regla.
Las siguientes fórmulas se pueden utilizar para evaluar integrales que involucran funciones logarítmicas.
\[\begin{align*} ∫x^{−1}\,dx &=\ln |x|+C \\[4pt] ∫\ln x\,\,dx &= x\ln x−x+C =x (\ln x−1)+C \\[4pt] ∫\log_a x\,dx &=\dfrac{x}{\ln a}(\ln x−1)+C \end{align*}\]
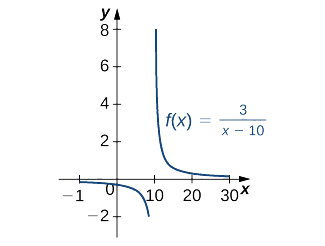
Encuentra la antiderivada de la función\(\dfrac{3}{x−10}. \)
Solución
Primero factoriza el\(3\) exterior del símbolo integral. Entonces usa la\(u^{−1}\) regla. Así,
\[∫\dfrac{3}{x−10}\,dx=3∫\dfrac{1}{x−10}\,dx=3∫\dfrac{du}{u}=3\ln |u|+C=3\ln |x−10|+C,\quad x≠10. \nonumber \]
Ver Figura\(\PageIndex{3}\).
Encuentra el antiderivado de\(\dfrac{1}{x+2}.\)
- Pista
-
Sigue el patrón de Ejemplo\(\PageIndex{9}\) para resolver el problema.
- Contestar
-
\(\displaystyle \int \dfrac{1}{x+2}\,dx = \ln |x+2|+C\)
Encuentra el antiderivado de\(\dfrac{2x^3+3x}{x^4+3x^2}. \)
Solución
Esto se puede reescribir como Sustitución de\(\displaystyle ∫(2x^3+3x)(x^4+3x^2)^{−1}\,dx.\) uso.
Vamos\(u=x^4+3x^2\), luego\(du=(4x^3+6x)\,dx.\) Alter\(du\) factorizando el\(2\). Así,
\[du=(4x^3+6x)\,dx=2(2x^3+3x)\,dx \nonumber \]
\[\dfrac{1}{2}\,du=(2x^3+3x)\,dx. \nonumber \]
Reescribe el integrando en\(u\):
\[∫(2x^3+3x)(x^4+3x^2)^{−1}\,dx=\dfrac{1}{2}∫u^{−1}\,du. \nonumber \]
Entonces tenemos
\[\dfrac{1}{2}∫u^{−1}\,du=\dfrac{1}{2}\ln |u|+C=\dfrac{1}{2}\ln ∣x^4+3x^2∣+C. \nonumber \]
Encuentra el antiderivado de la función log\(\log_2 x.\)
Solución
Siga el formato en la fórmula listada en la regla sobre fórmulas de integración que involucran funciones logarítmicas. En base a este formato, tenemos
\[∫\log_2 x\,dx=\dfrac{x}{\ln 2}(\ln x−1)+C.\nonumber \]
Encuentra el antiderivado de\(\log_3 x\).
- Pista
-
Siga Ejemplo\(\PageIndex{11}\) y consulte la regla sobre fórmulas de integración que involucran funciones logarítmicas.
- Contestar
-
\(\displaystyle ∫\log_3 x\,dx=\dfrac{x}{\ln 3}(\ln x−1)+C\)
Ejemplo\(\PageIndex{12}\) es una integral definitiva de una función trigonométrica. Con funciones trigonométricas, a menudo tenemos que aplicar una propiedad trigonométrica o una identidad antes de poder avanzar. Encontrar la forma correcta del integrando suele ser la clave para una integración fluida.
Evaluar la integral definida\[∫^{π/2}_0\dfrac{\sin x}{1+\cos x}\,dx.\nonumber \]
Solución
Necesitamos sustitución para evaluar este problema. Que\(u=1+\cos x\) así\(du=−\sin x\,\,dx.\)
Reescribir la integral en términos de\(u\), cambiando los límites de la integración también. Así,
\[ \begin{align*} u &= 1+\cos(0)=2 \\[4pt] u &=1+\cos \left(\dfrac{π}{2}\right)=1.\end{align*}\]
Entonces
\[ \begin{align*}∫^{π/2}_0\dfrac{\sin x}{1+\cos x} &=−∫^1_2 u^{−1}\,du \\[4pt] &=∫^2_1u^{−1}\,du \\[4pt] &=\ln |u|\,\bigg|^2_1 \\[4pt] &=[\ln 2−\ln 1]=\ln 2 \end{align*}\]
Conceptos clave
- Las funciones exponenciales y logarítmicas surgen en muchas aplicaciones del mundo real, especialmente aquellas que involucran crecimiento y decadencia.
- La sustitución se utiliza a menudo para evaluar integrales que involucran funciones exponenciales o logaritmos.
Ecuaciones Clave
- Integrales de funciones exponenciales
\[∫e^x\,dx=e^x+C \nonumber \]
\[\int a^x\,dx=\dfrac{a^x}{\ln a}+C \nonumber \]
- Fórmulas de integración que implican funciones logarí
\[∫x^{−1}\,dx=\ln |x|+C \nonumber \]
\[∫\ln x\,dx=x\ln x−x+C=x(\ln x−1)+C \nonumber \]
\[∫\log_a x\,dx=\dfrac{x}{\ln a}(\ln x−1)+C \nonumber \]


