4.2: Aproximaciones lineales y diferenciales
- Page ID
- 116438
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Describir la aproximación lineal a una función en un punto.
- Escribir la linealización de una función dada.
- Dibuja una gráfica que ilustre el uso de diferenciales para aproximar el cambio en una cantidad.
- Calcular el error relativo y el error porcentual en el uso de una aproximación diferencial.
Acabamos de ver cómo los derivados nos permiten comparar cantidades relacionadas que van cambiando con el tiempo. En esta sección, examinamos otra aplicación de derivados: la capacidad de aproximar funciones localmente por funciones lineales. Las funciones lineales son las funciones más fáciles con las que trabajar, por lo que proporcionan una herramienta útil para aproximar valores de función. Además, las ideas presentadas en esta sección se generalizan posteriormente en el texto cuando estudiamos cómo aproximar funciones por polinomios de grado superior Introducción a las Series y Funciones de Potencia.
Aproximación lineal de una función en un punto
Considerar una función\(f\) que sea diferenciable en un punto\(x=a\). Recordemos que la línea tangente a la gráfica de\(f\) at\(a\) viene dada por la ecuación
\[y=f(a)+f'(a)(x−a). \nonumber \]
Por ejemplo, considere la función\(f(x)=\frac{1}{x}\) en\(a=2\). Ya que\(f\) es diferenciable en\(x=2\) y\(f'(x)=−\frac{1}{x^2}\), vemos eso\(f'(2)=−\frac{1}{4}\). Por lo tanto, la línea tangente a la gráfica de\(f\) at\(a=2\) viene dada por la ecuación
\[y=\frac{1}{2}−\frac{1}{4}(x−2). \nonumber \]
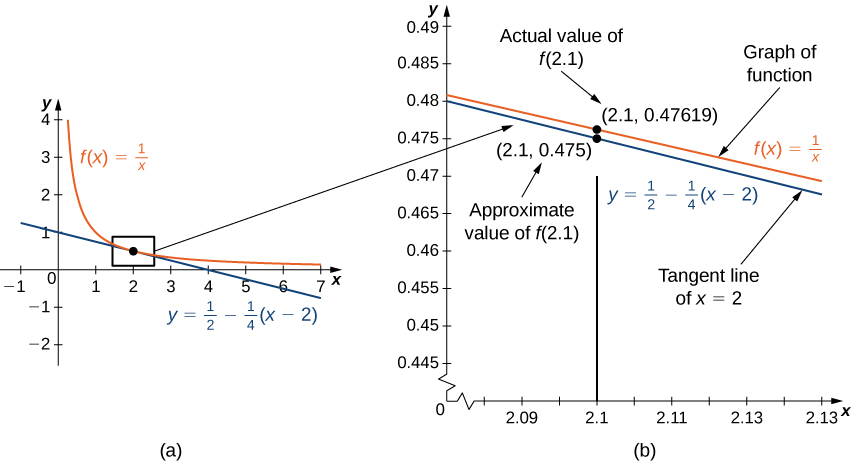
La figura\(\PageIndex{1a}\) muestra una gráfica de\(f(x)=\frac{1}{x}\) junto con la línea tangente a\(f\) at\(x=2\). Tenga en cuenta que para\(x\) cerca\(2\), la gráfica de la línea tangente está cerca de la gráfica de\(f\). Como resultado, podemos usar la ecuación de la línea tangente\(f(x)\) para aproximar para\(x\) cerca\(2\). Por ejemplo, si\(x=2.1\), el\(y\) valor del punto correspondiente en la línea tangente es
\[y=\frac{1}{2}−\frac{1}{4}(2.1−2)=0.475. \nonumber \]
El valor real de\(f(2.1)\) viene dado por
\[f(2.1)=\frac{1}{2.1}≈0.47619. \nonumber \]
Por lo tanto, la línea tangente nos da una aproximación bastante buena de\(f(2.1)\) (Figura\(\PageIndex{1b}\)). No obstante, tenga en cuenta que para valores de\(x\) lejos de\(2\), la ecuación de la línea tangente no nos da una buena aproximación. Por ejemplo, si\(x=10\), el\(y\) -valor del punto correspondiente en la línea tangente es
\[y=\frac{1}{2}−\frac{1}{4}(10−2)=\frac{1}{2}−2=−1.5, \nonumber \]
mientras que el valor de la función at\(x=10\) es\(f(10)=0.1.\)
En general, para una función diferenciable\(f\), la ecuación de la línea tangente a\(f\) at se\(x=a\) puede utilizar para aproximarse\(f(x)\) para\(x\) cerca\(a\). Por lo tanto, podemos escribir
\(f(x)≈f(a)+f'(a)(x−a)\)para\(x\) cerca\(a\).
Llamamos a la función lineal
\[L(x)=f(a)+f'(a)(x−a) \label{linearapprox} \]
la aproximación lineal, o aproximación de línea tangente, de\(f\) at\(x=a\). Esta función también\(L\) se conoce como la linealización de\(f\) at\(x=a.\)
Para mostrar cuán útil puede ser la aproximación lineal, observamos cómo encontrar la aproximación lineal para\(f(x)=\sqrt{x}\) en\(x=9.\)
Encuentra la aproximación lineal de\(f(x)=\sqrt{x}\) at\(x=9\) y usa la aproximación para estimar\(\sqrt{9.1}\).
Solución
Ya que estamos buscando la aproximación lineal al\(x=9,\) usar la ecuación\ ref {linearapprox} sabemos que la aproximación lineal viene dada por
\[L(x)=f(9)+f'(9)(x−9). \nonumber \]
Tenemos que encontrar\(f(9)\) y\(f'(9).\)
\(f(x)=\sqrt{x}⇒f(9)=\sqrt{9}=3\)
\(f'(x)=\frac{1}{2\sqrt{x}}⇒f'(9)=\frac{1}{2\sqrt{9}}=\frac{1}{6}\)
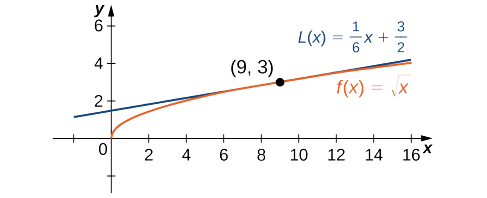
Por lo tanto, la aproximación lineal viene dada por la Figura\(\PageIndex{2}\).
\[L(x)=3+\frac{1}{6}(x−9) \nonumber \]
Usando la aproximación lineal, podemos estimar\(\sqrt{9.1}\) escribiendo
\[\sqrt{9.1}=f(9.1)≈L(9.1)=3+\frac{1}{6}(9.1−9)≈3.0167. \nonumber \]
Análisis
Usando una calculadora, el valor de\(\sqrt{9.1}\) a cuatro decimales es\(3.0166\). El valor dado por la aproximación lineal,\(3.0167\), es muy cercano al valor obtenido con una calculadora, por lo que parece que usar esta aproximación lineal es una buena manera de estimar\(\sqrt{x}\), al menos para x cerca\(9\). Al mismo tiempo, puede parecer extraño usar una aproximación lineal cuando solo podemos presionar algunos botones en una calculadora para evaluar\(\sqrt{9.1}\). Sin embargo, ¿cómo evalúa la calculadora\(\sqrt{9.1}\)? ¡La calculadora usa una aproximación! De hecho, las calculadoras y las computadoras utilizan aproximaciones todo el tiempo para evaluar expresiones matemáticas; solo usan aproximaciones de mayor grado.
Encuentra la aproximación lineal local a\(f(x)=\sqrt[3]{x}\) at\(x=8\). Úselo para aproximarse\(\sqrt[3]{8.1}\) a cinco decimales.
- Pista
-
\(L(x)=f(a)+f'(a)(x−a)\)
- Responder
-
\(L(x)=2+\frac{1}{12}(x−8);\)\(2.00833\)
Encuentra la aproximación lineal de\(f(x)=\sin x \) at\(x=\frac{π}{3}\) y úsalo para aproximar\(\sin(62°).\)
Solución
Primero observamos que dado que\(\frac{π}{3}\) rad es equivalente a\(60°\), usar la aproximación lineal a\(x=π/3\) parece razonable. La aproximación lineal viene dada por
\(L(x)=f(\frac{π}{3})+f'(\frac{π}{3})(x−\frac{π}{3}).\)
Vemos que
\(f(x)=\sin x ⇒f(\frac{π}{3})=\sin(\frac{π}{3})=\frac{\sqrt{3}}{2}\)
\(f'(x)=\cos x ⇒f'(\frac{π}{3})=\cos(\frac{π}{3})=\frac{1}{2}\)
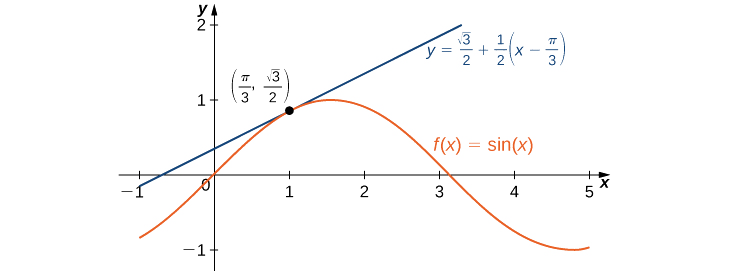
Por lo tanto, la aproximación lineal de\(f\) at\(x=π/3\) viene dada por la Figura\(\PageIndex{3}\).
\(L(x)=\frac{\sqrt{3}}{2}+\frac{1}{2}(x−\frac{π}{3})\)
Para estimar\(\sin(62°)\) usando\(L\), primero debemos convertir\(62°\) a radianes. Tenemos\(62°=\frac{62π}{180}\) radianes, por lo que la estimación para\(\sin(62°)\) viene dada por
\(\sin(62°)=f(\frac{62π}{180})≈L(\frac{62π}{180})=\frac{\sqrt{3}}{2}+\frac{1}{2}(\frac{62π}{180}−\frac{π}{3})=\frac{\sqrt{3}}{2}+\frac{1}{2}(\frac{2π}{180})=\frac{\sqrt{3}}{2}+\frac{π}{180}≈0.88348.\)
Encuentre la aproximación lineal para\(f(x)=\cos x \) en\(x=\frac{π}{2}.\)
- Pista
-
\(L(x)=f(a)+f'(a)(x−a)\)
- Responder
-
\(L(x)=−x+\frac{π}{2}\)
Las aproximaciones lineales pueden ser utilizadas en la estimación de raíces y potencias. En el siguiente ejemplo, encontramos la aproximación lineal para\(f(x)=(1+x)^n\) at\(x=0\), que puede ser utilizada para estimar raíces y potencias para números reales cercanos\(1\). La misma idea puede extenderse a una función de la forma\(f(x)=(m+x)^n\) para estimar raíces y potencias cercanas a un número diferente\(m\).
Encuentra la aproximación lineal de\(f(x)=(1+x)^n\) at\(x=0\). Utilice esta aproximación para estimar\((1.01)^3.\)
Solución
La aproximación lineal a\(x=0\) viene dada por
\(L(x)=f(0)+f'(0)(x−0).\)
Porque
\(f(x)=(1+x)^n⇒f(0)=1\)
\(f'(x)=n(1+x)^{n−1}⇒f'(0)=n,\)
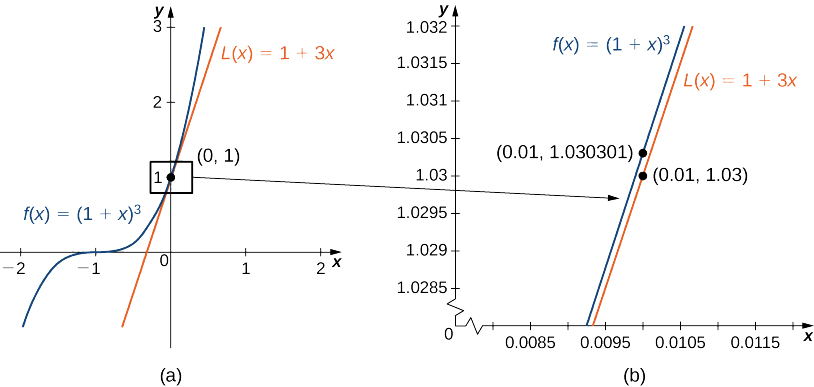
la aproximación lineal viene dada por la Figura\(\PageIndex{4a}\).
\(L(x)=1+n(x−0)=1+nx\)
Podemos aproximar\((1.01)^3\) evaluando\(L(0.01)\) cuándo\(n=3\). Concluimos que
\((1.01)^3=f(1.01)≈L(1.01)=1+3(0.01)=1.03.\)
Encuentra la aproximación lineal de\(f(x)=(1+x)^4\) at\(x=0\) sin usar el resultado del ejemplo anterior.
- Pista
-
\(f'(x)=4(1+x)^3\)
- Responder
-
\(L(x)=1+4x\)
Diferenciales
Hemos visto que las aproximaciones lineales pueden ser utilizadas para estimar los valores de las funciones. También se pueden utilizar para estimar la cantidad que cambia un valor de función como resultado de un pequeño cambio en la entrada. Para discutirlo de manera más formal, definimos un concepto relacionado: los diferenciales. Los diferenciales nos proporcionan una manera de estimar la cantidad que cambia una función como resultado de un pequeño cambio en los valores de entrada.
Cuando miramos por primera vez derivados, utilizamos la notación Leibniz\(dy/dx\) para representar la derivada de\(y\) con respecto a\(x\). A pesar de que usamos las expresiones\(dy\) y\(dx\) en esta notación, no tenían sentido por sí mismas. Aquí vemos un significado a las expresiones\(dy\) y\(dx\). Supongamos que\(y=f(x)\) es una función diferenciable. \(dx\)Sea una variable independiente a la que se le pueda asignar cualquier número real distinto de cero, y definir la variable dependiente\(dy\) por
\[dy=f'(x)\,dx. \label{diffeq} \]
Es importante notar que\(dy\) es una función de ambos\(x\) y\(dx\). Las expresiones\(dy\) y\(dx\) se llaman diferenciales. Podemos dividir ambos lados de la Ecuación\ ref {diffeq} por la\(dx,\) cual rinde
\[\frac{dy}{dx}=f'(x). \label{inteq} \]
Esta es la expresión familiar que hemos utilizado para denotar un derivado. La ecuación\ ref {inteq} se conoce como la forma diferencial de la ecuación\ ref {diffeq}.
Para cada una de las siguientes funciones, encontrar\(dy\) y evaluar cuándo\(x=3\) y\(dx=0.1.\)
- \(y=x^2+2x\)
- \(y=\cos x \)
Solución
El paso clave es calcular la derivada. Cuando tenemos eso, podemos obtener\(dy\) directamente.
a. ya que\(f(x)=x^2+2x,\) sabemos\(f'(x)=2x+2\), y por lo tanto
\(dy=(2x+2)\,dx.\)
Cuándo\(x=3\) y\(dx=0.1,\)
\(dy=(2⋅3+2)(0.1)=0.8.\)
b. ya que\(f(x)=\cos x , f'(x)=−\sin(x).\) esto nos da
\(dy=−\sin x \,dx.\)
Cuándo\(x=3\) y\(dx=0.1,\)
\(dy=−\sin(3)(0.1)=−0.1\sin(3).\)
Para\(y=e^{x^2}\), encontrar\(dy\).
- Pista
-
\(dy=f'(x)\,dx\)
- Responder
-
\(dy=2xe^{x^2}dx\)
Ahora conectamos diferenciales a aproximaciones lineales. Los diferenciales se pueden utilizar para estimar el cambio en el valor de una función resultante de un pequeño cambio en los valores de entrada. Considerar una función\(f\) que sea diferenciable en el punto\(a\). Supongamos que la entrada\(x\) cambia en una pequeña cantidad. Nos interesa cuánto\(y\) cambia la salida. Si\(x\) cambia de\(a\) a\(a+dx\), entonces el cambio en\(x\) es\(dx\) (también denotado\(Δx\)), y el cambio en\(y\) viene dado por
\[Δy=f(a+dx)−f(a). \nonumber \]
En lugar de calcular el cambio exacto en\(y\), sin embargo, a menudo es más fácil aproximar el cambio en\(y\) usando una aproximación lineal. Para\(x\) cerca se\(a, f(x)\) puede aproximar por la aproximación lineal (Ecuación\ ref {linearapprox})
\[L(x)=f(a)+f'(a)(x−a). \nonumber \]
Por lo tanto, si\(dx\) es pequeño,
\[f(a+dx)≈L(a+dx)=f(a)+f'(a)(a+dx−a). \nonumber \]
Es decir,
\[f(a+dx)−f(a)≈L(a+dx)−f(a)=f'(a)\,dx. \nonumber \]
En otras palabras, el cambio real en la función\(f\) si\(x\) aumenta de\(a\) a\(a+dx\) es aproximadamente la diferencia entre\(L(a+dx)\) y\(f(a)\), donde\(L(x)\) está la aproximación lineal de\(f\) at\(a\). Por definición de\(L(x)\), esta diferencia es igual a\(f'(a)\,dx\). En resumen,
\[Δy=f(a+dx)−f(a)≈L(a+dx)−f(a)=f'(a)\,dx=dy. \nonumber \]
Por lo tanto, podemos utilizar el diferencial\(dy=f'(a)\,dx\) para aproximar el cambio en\(y\) si\(x\) aumenta de\(x=a\) a\(x=a+dx\). Esto lo podemos ver en la siguiente gráfica.
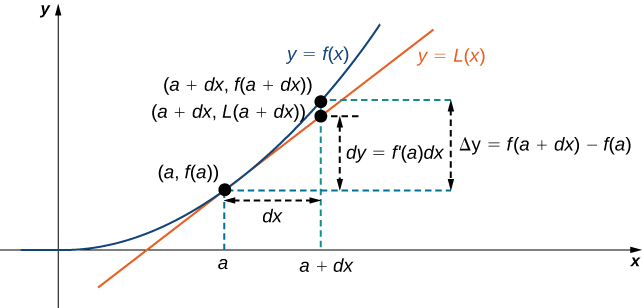
Ahora echamos un vistazo a cómo usar diferenciales para aproximar el cambio en el valor de la función que resulta de un pequeño cambio en el valor de la entrada. Tenga en cuenta que el cálculo con diferenciales es mucho más sencillo que calcular valores reales de funciones y el resultado es muy cercano a lo que obtendríamos con el cálculo más exacto.
Let\(y=x^2+2x.\) Compute\(Δy\) y\(dy\) en\(x=3\) si\(dx=0.1.\)
Solución
El cambio real en\(y\) si\(x\) cambia de\(x=3\) a\(x=3.1\) viene dado por
\(Δy=f(3.1)−f(3)=[(3.1)^2+2(3.1)]−[3^2+2(3)]=0.81.\)
El cambio aproximado en\(y\) viene dado por\(dy=f'(3)\,dx\). Ya\(f'(x)=2x+2,\) que tenemos
\(dy=f'(3)\,dx=(2(3)+2)(0.1)=0.8.\)
Para\(y=x^2+2x,\) encontrar\(Δy\) y\(dy\) en\(x=3\) si\(dx=0.2.\)
- Pista
-
\(dy=f'(3)\,dx, \;Δy=f(3.2)−f(3)\)
- Responder
-
\(dy=1.6, \; Δy=1.64\)
Cálculo de la cantidad de error
Cualquier tipo de medición es propenso a una cierta cantidad de error. En muchas aplicaciones, ciertas cantidades se calculan en base a mediciones. Por ejemplo, el área de un círculo se calcula midiendo el radio del círculo. Un error en la medición del radio conduce a un error en el valor calculado del área. Aquí examinamos este tipo de error y estudiamos cómo se pueden utilizar los diferenciales para estimar el error.
Considera una función\(f\) con una entrada que es una cantidad medida. Supongamos que el valor exacto de la cantidad medida es\(a\), pero el valor medido es\(a+dx\). Decimos que el error de medición es\(dx\) (o\(Δx\)). Como resultado, se produce un error en la cantidad calculada\(f(x)\). Este tipo de error se conoce como error propagado y viene dado por
\[Δy=f(a+dx)−f(a). \nonumber \]
Dado que todas las mediciones son propensas a algún grado de error, no conocemos el valor exacto de una cantidad medida, por lo que no podemos calcular exactamente el error propagado. Sin embargo, dada una estimación de la precisión de una medición, podemos usar diferenciales para aproximar el error propagado\(Δy.\) Específicamente, si\(f\) es una función diferenciable en\(a\), el error propagado es
\[Δy≈dy=f'(a)\,dx. \nonumber \]
Desafortunadamente, no conocemos el valor exacto\(a.\) Sin embargo, podemos usar el valor medido\(a+dx,\) y estimar
\[Δy≈dy≈f'(a+dx)\,dx. \nonumber \]
En el siguiente ejemplo, observamos cómo se pueden utilizar los diferenciales para estimar el error en el cálculo del volumen de una caja si asumimos que la medición de la longitud lateral se realiza con cierta precisión.
Supongamos que la longitud lateral de un cubo se mide para ser\(5\) cm con una precisión de\(0.1\) cm.
- Utilice diferenciales para estimar el error en el volumen calculado del cubo.
- Calcular el volumen del cubo si la longitud lateral es (i)\(4.9\) cm y (ii)\(5.1\) cm para comparar el error estimado con el error potencial real.
Solución
a. La medida de la longitud lateral es precisa dentro de\(±0.1\) cm. Por lo tanto,
\(−0.1≤dx≤0.1.\)
El volumen de un cubo viene dado por\(V=x^3\), lo que lleva a
\(dV=3x^2dx.\)
Usando la longitud lateral medida de\(5\) cm, podemos estimar que
\(−3(5)^2(0.1)≤dV≤3(5)^2(0.1).\)
Por lo tanto,
\(−7.5≤dV≤7.5.\)
b. Si la longitud lateral es realmente\(4.9\) cm, entonces el volumen del cubo es
\(V(4.9)=(4.9)^3=117.649\text{cm}^3.\)
Si la longitud lateral es en realidad\(5.1\) cm, entonces el volumen del cubo es
\(V(5.1)=(5.1)^3=132.651\text{cm}^3.\)
Por lo tanto, el volumen real del cubo está entre\(117.649\) y\(132.651\). Dado que la longitud lateral se mide para ser de 5 cm, el volumen calculado es\(V(5)=5^3=125.\) Por lo tanto, el error en el volumen calculado es
\(117.649−125≤ΔV≤132.651−125.\)
Es decir,
\(−7.351≤ΔV≤7.651.\)
Vemos que el error estimado\(dV\) es relativamente cercano al error potencial real en el volumen calculado.
Estimar el error en el volumen calculado de un cubo si la longitud lateral se mide para ser\(6\) cm con una precisión de\(0.2\) cm.
- Pista
-
\(dV=3x^2dx\)
- Responder
-
La medición del volumen es precisa dentro\(21.6\,\text{cm}^3\).
El error de medición\(dx\ (=Δx)\) y el error propagado\(Δy\) son errores absolutos. Normalmente nos interesa el tamaño de un error relativo al tamaño de la cantidad que se mide o calcula. Dado un error absoluto\(Δq\) para una cantidad en particular, definimos el error relativo como\(\frac{Δq}{q}\), donde\(q\) está el valor real de la cantidad. El error porcentual es el error relativo expresado como porcentaje. Por ejemplo, si medimos la altura de una escalera para estar\(63\) en. cuando la altura real está\(62\) en., el error absoluto es de 1 pulg. pero el error relativo es\(\frac{1}{62}=0.016\), o\(1.6\%\). En comparación, si medimos el ancho de una pieza de cartón para estar\(8.25\) en. cuando el ancho real está\(8\) en., nuestro error absoluto está\(\frac{1}{4}\) en., mientras que el error relativo es\(\frac{0.25}{8}=\frac{1}{32}\), o\(3.1\%.\) Por lo tanto, el error porcentual en la medición del cartón es mayor, incluso aunque\(0.25\) en. es menor que\(1\) en.
Un astronauta que usa una cámara mide el radio de la Tierra como\(4000\) mi con un error de\(±80\) mi. Usemos diferenciales para estimar el error relativo y porcentual de usar esta medición de radio para calcular el volumen de la Tierra, asumiendo que el planeta es una esfera perfecta.
Solución: Si la medición del radio es precisa dentro\(±80,\) tenemos
\(−80≤dr≤80.\)
Dado que el volumen de una esfera viene dado por\(V=(\frac{4}{3})πr^3,\) tenemos
\(dV=4πr^2dr.\)
Usando el radio medido de\(4000\) mi, podemos estimar
\(−4π(4000)^2(80)≤dV≤4π(4000)^2(80).\)
Para estimar el error relativo, considere\(\dfrac{dV}{V}\). Como no conocemos el valor exacto del volumen\(V\), utilice el radio medido\(r=4000\) mi para estimar\(V\). Obtenemos\(V≈(\frac{4}{3})π(4000)^3\). Por lo tanto, el error relativo satisface
\(\frac{−4π(4000)^2(80)}{4π(4000)^3/3}≤\dfrac{dV}{V}≤\frac{4π(4000)^2(80)}{4π(4000)^3/3},\)
lo que simplifica a
\(−0.06≤\dfrac{dV}{V}≤0.06.\)
El error relativo es\(0.06\) y el error porcentual es\(6\%\).
Determinar el porcentaje de error si el radio de la Tierra se mide para ser\(3950\) mi con un error de\(±100\) mi.
- Pista
-
Usa el hecho de que\(dV=4πr^2dr\) para encontrar\(dV/V\).
- Responder
-
\(7.6\%\)
Conceptos clave
- Una función diferenciable\(y=f(x)\) puede ser aproximada\(a\) por la función lineal
\(L(x)=f(a)+f'(a)(x−a).\)
- Para una función\(y=f(x)\), si\(x\) cambia de\(a\) a\(a+dx\), entonces
\(dy=f'(x)\,dx\)
es una aproximación para el cambio en\(y\). El cambio real en\(y\) es
\(Δy=f(a+dx)−f(a).\)
- Un error de medición\(dx\) puede conducir a un error en una cantidad calculada\(f(x)\). El error en la cantidad calculada se conoce como el error propagado. El error propagado puede ser estimado por
\(dy≈f'(x)\,dx.\)
- Para estimar el error relativo de una cantidad en particular\(q\), estimamos\(\frac{Δq}{q}\).
Ecuaciones Clave
- Aproximación lineal
\(L(x)=f(a)+f'(a)(x−a)\)
- Un diferencial
\(dy=f'(x)\,dx\)
Glosario
- diferencial
- el diferencial\(dx\) es una variable independiente a la que se le puede asignar cualquier número real distinto de cero; el diferencial\(dy\) se define como\(dy=f'(x)\,dx\)
- forma diferencial
- dada una función diferenciable\(y=f'(x),\) la ecuación\(dy=f'(x)\,dx\) es la forma diferencial de la derivada de\(y\) con respecto a\(x\)
- aproximación lineal
- la función lineal\(L(x)=f(a)+f'(a)(x−a)\) es la aproximación lineal de\(f\) at\(x=a\)
- porcentaje de error
- el error relativo expresado como porcentaje
- error propagado
- el error que da como resultado una cantidad calculada\(f(x)\) resultante de un error de medición\(dx\)
- error relativo
- dado un error absoluto\(Δq\) para una cantidad particular,\(\frac{Δq}{q}\) es el error relativo.
- aproximación de línea tangente (linealización)
- ya que la aproximación lineal de\(f\) at\(x=a\) se define usando la ecuación de la línea tangente, la aproximación lineal de\(f\) at también\(x=a\) se conoce como la aproximación de la línea tangente a\(f\) at\(x=a\)


