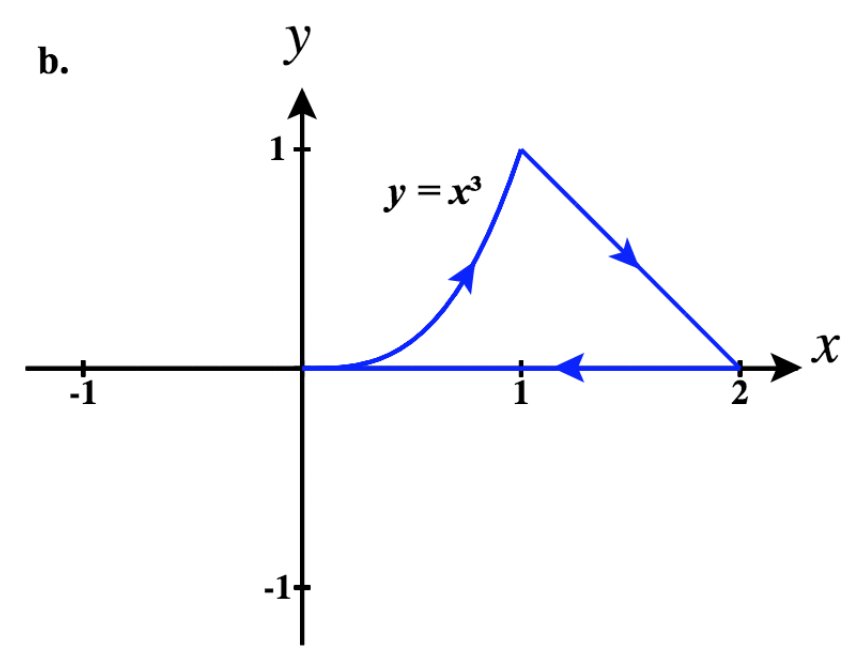
13.1E: Ejercicios para la Sección 13.1
( \newcommand{\kernel}{\mathrm{null}\,}\)
Introducción a las funciones vectorizadas
1) Dar las funciones del componentex=f(t) yy=g(t) para la función de valor vectorial⇀r(t)=3sectˆi+2tantˆj.
- Contestar
- Aquí podemos decir esof(t)=3sect,g(t)=2tant
así lo tenemosx(t)=3sect,y(t)=2tant.
2) Dado⇀r(t)=3sectˆi+2tantˆj, encuentre los siguientes valores (si es posible).
- ⇀r(π4)
- ⇀r(π)
- ⇀r(π2)
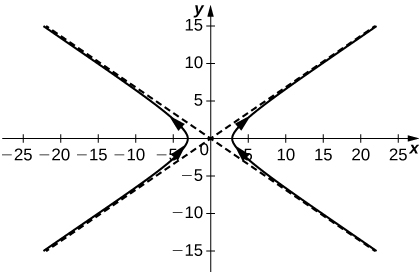
3) Esbozar la curva de la función vectorizada⇀r(t)=3sectˆi+2tantˆj y dar la orientación de la curva. Esbozar asíntotas como guía para la gráfica.
- Contestar
Límites de las funciones valoradas por vectores
4) Evaluarlimt→0(etˆi+sinttˆj+e−tˆk)
5) Dada la función vector-valuada⇀r(t)=⟨cost,sint⟩ encontrar los siguientes valores:
- limt→π4⇀r(t)
- ⇀r(π3)
- ¿Es⇀r(t) continuo ent=π3?
- Gráfica⇀r(t).
- Contestar
-
a.⟨√22,√22⟩,
b.⟨12,√32⟩,
c. Sí, el límite a medida que tπ3 se acerca es igual ar(π3),
d.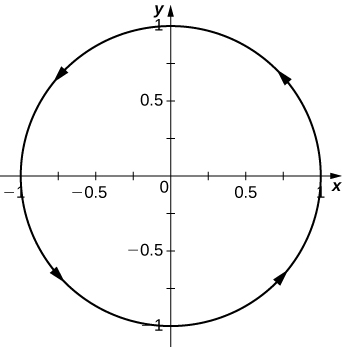
6) Dada la función vectorizada⇀r(t)=⟨t,t2+1⟩, encuentre los siguientes valores:
- limt→−3⇀r(t)
- ⇀r(−3)
- ¿Es⇀r(t) continuo enx=−3?
- ⇀r(t+2)−⇀r(t)
7) Dejar⇀r(t)=etˆi+sintˆj+lntˆk. Encuentra los siguientes valores:
- ⇀r(π4)
- limt→π4⇀r(t)
- ¿Es⇀r(t) continuo ent=π4?
- Contestar
- a.eπ4,√22,ln(π4) ⟩;
b.eπ4,√22,ln(π4) ⟩;
c. Si
Para los ejercicios 8 - 13, encuentre el límite de las siguientes funciones vectorizadas en el valor indicado det.
8)limt→4⟨√t−3,√t−2t−4,tan(πt)⟩
9)limt→π2⇀r(t) para⇀r(t)=etˆi+sintˆj+lntˆk
- Contestar
- ⟨eπ2,1,ln(π2)⟩
10)limt→∞⟨e−2t,2t+33t−1,arctan(2t)⟩
11)limt→e2⟨tln(t),lntt2,√ln(t2)⟩
- Contestar
- 2e2ˆi+2e4ˆj+2ˆk
12)limt→π6⟨cos2t,sin2t,1⟩
13)limt→∞⇀r(t) para⇀r(t)=2e−ti+e−tˆj+ln(t−1)ˆk
- Contestar
- El límite no existe porque el límite deln(t−1) como set acerca al infinito no existe.
Dominio de una función valorada por vector
Para los problemas 14 - 17, encuentre el dominio de las funciones vectorizadas.
14) Dominio:⇀r(t)=⟨t2,t,sint⟩
15) Dominio:⇀r(t)=⟨t2,tant,lnt⟩
- Contestar
- D⇀r={t|t>0,t≠(2k+1)π2,wherekis any integer}
16) Dominio:⇀r(t)=⟨t2,√t−3,32t+1⟩
17) Dominio:⇀r(t)=⟨csc(t),1√t−3,ln(t−2)⟩
- Contestar
- D⇀r={t|t>3,t≠nπ,wherenis any integer}
18) a. encontrar el dominio de⇀r(t)=2e−tˆi+e−tˆj+ln(t−1)ˆk.
b. ¿Para qué valores det es⇀r(t)=2e−tˆi+e−tˆj+ln(t−1)ˆk continuo?
- Contestar
- a.D⇀r:(1,∞)
b. Todot tal quet∈(1,∞)
19) Dominio:⇀r(t)=(arccost)ˆi+√2t−1ˆj+ln(t)ˆk
- Contestar
- D⇀r:[12,1]
Visualización de funciones valoradas por vectores
20) Describir la curva definida por la función vectorizada⇀r(t)=(1+t)ˆi+(2+5t)ˆj+(−1+6t)ˆk.
21) Déjalo⇀r(t)=⟨cost,t,sint⟩ y utilízalo para responder a las siguientes preguntas.
- ¿Para qué valores det es⇀r(t) continuo?
- Esbozar la gráfica de⇀r(t).
- Contestar
- a.⇀r es continuo para todos los números reales, es decir, parat∈R.
b. tenga en cuenta que debe haber az en el eje vertical en la sección transversal en la imagen (a) de abajo en lugar de lay.
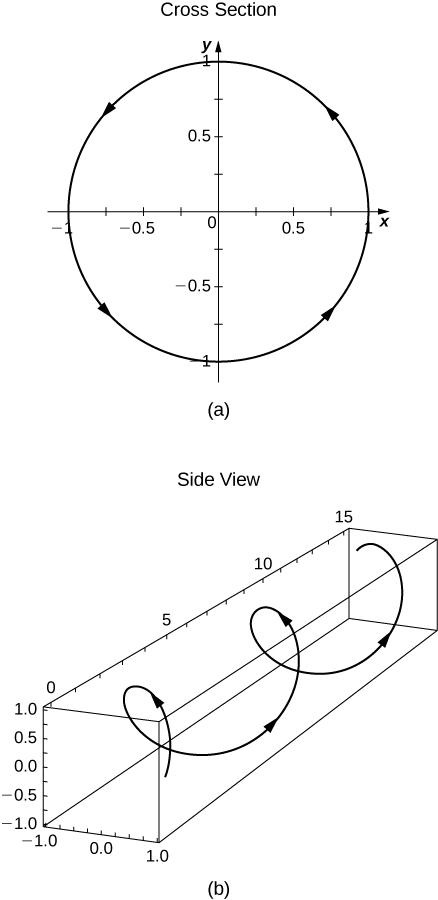
22) Producir un boceto cuidadoso de la gráfica de⇀r(t)=t2ˆi+tˆj.
En las preguntas 23 a 25, utilice una utilidad gráfica para esbozar cada una de las funciones vectorizadas:
23) [T]⇀r(t)=2cos2tˆi+(2−√t)ˆj
- Contestar
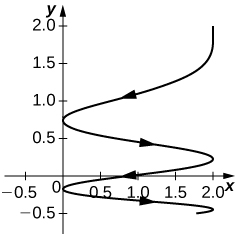
24) [T]⇀r(t)=⟨ecos(3t),e−sin(t)⟩
25) [T]⇀r(t)=⟨2−sin(2t),3+2cost⟩
- Contestar
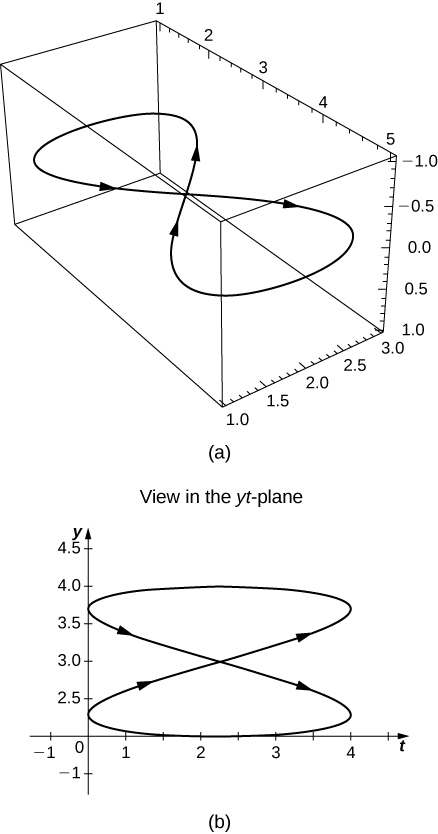
Encontrar ecuaciones enx yy para la trayectoria trazada por funciones vectorizadas
Para las preguntas 26-33, elimine el parámetrot, escriba la ecuación en coordenadas cartesianas, luego esboce la gráfica de las funciones vectorizadas.
26)⇀r(t)=2tˆi+t2ˆj
(Pista: Dejarx=2t yy=t2. Resolver la primera ecuación parat en términos dex y sustituir este resultado en la segunda ecuación.)
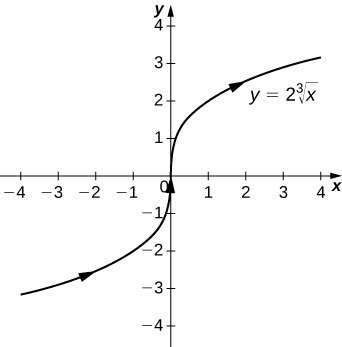
27)⇀r(t)=t3ˆi+2tˆj
- Contestar
-
y=23√x, una variación de la función de raíz de cubo
28)⇀r(t)=sintˆi+costˆj
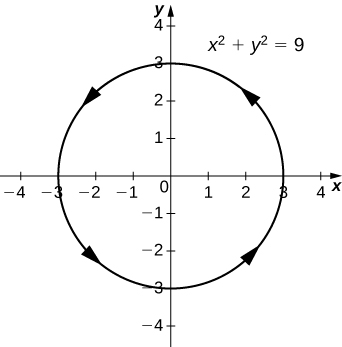
29)⇀r(t)=3costˆi+3sintˆj
- Contestar
-
x2+y2=9, un círculo centrado en(0,0) un radio 3 y una orientación en sentido contrario a las agujas del reloj
30)⇀r(t)=⟨sint,4cost⟩
31)⇀r(t)=2sintˆi−3costˆj
- Contestar
-
x24+y29=1, una elipse centrada en(0,0) con intercepciones enx=±2 yy=±3, y una orientación en el sentido de las agujas del reloj
32)⇀r(t)=tantˆi−2sectˆj
33)⇀r(t)=3sectˆi+4tantˆj
- Contestar
-
x29−y216=1, una hipérbola centrada en(0,0) conx -intercepciones(3,0) y(−3,0), con orientación mostrada
Encontrar una función con valor vectorial para trazar la gráfica de una ecuación enx yy
Para las preguntas 34 - 40, busque una función de valor vectorial que rastrea la curva dada en la dirección indicada.
34)4x2+9y2=36; en sentido horario y antihorario
35)y=x2; de izquierda a derecha
- Contestar
- ⇀r(t)=⟨t,t2⟩, dondet aumenta
36) La línea a travésP yQ dóndeP está(1,4,−2) yQ es(3,9,6)
37) El círculo,x2+y2=36, orientado a las agujas del reloj, con posición(−6,0) en el tiempot=0.
- Contestar
- ⇀r(t)=−6costˆi+6sintˆj
38) La elipse,x2+y236=1, orientada en sentido antihorario
- Contestar
- ⇀r(t)=costˆi+6sintˆj
39) La hipérbolay236−x2=1, pieza superior está orientada de izquierda a derecha
- Contestar
- ⇀r(t)=tantˆi+6sectˆj
40) La hipérbola,x249−y264=1, la pieza derecha está orientada de abajo hacia arriba
- Contestar
- ⇀r(t)=7sectˆi+8tantˆj
Parametrización de una ruta por tramos
Para las preguntas 41 a 44, proporcione una parametrización para cada ruta por tramos. Intenta escribir una parametrización que comience cont=0 y progrese a través de valores de at medida que te mueves de una pieza a otra.
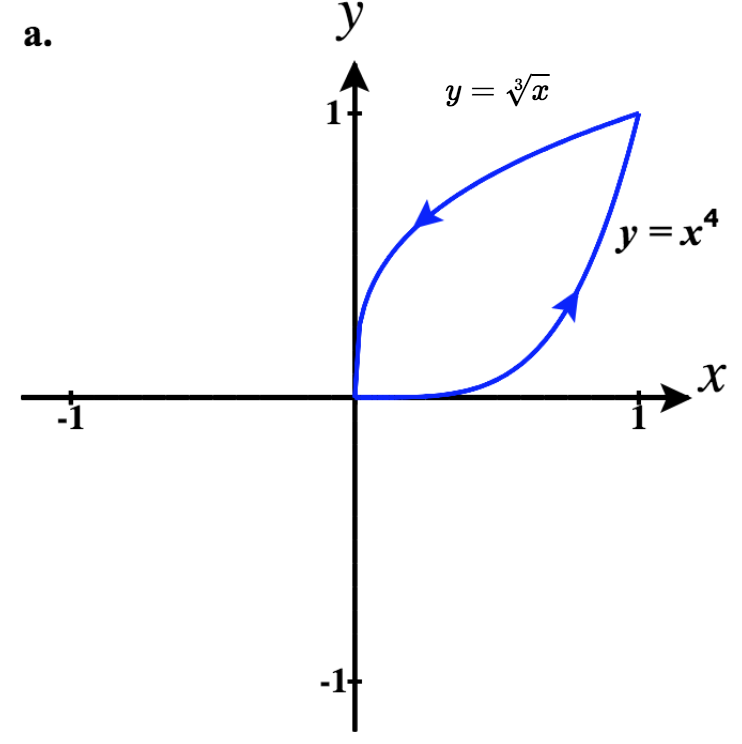
41)
- Contestar
- a.⇀r1(t)=tˆi+t4ˆj for0≤t≤1
⇀r2(t)=−tˆi+3√−tˆj for−1≤t≤0
Así que una parametrización por partes de esta ruta es:
\ (\ vecs r (t) =\ begin {cases}
t\,\ hat {\ mathbf {i}} + t^4\,\ hat {\ mathbf {j}}, & 0\ le t\ le 1\\
\ left (2-t\ right)\,\ hat {\ mathbf {i}} +\ sqrt [3] {2-t}\,\ hat {\ mathbf {j}}, & 1\ lt t\ le 2
\ end {cases}\)
b.⇀r1(t)=tˆi+3√tˆj for0≤t≤1
⇀r2(t)=−tˆi+(−t)4ˆj for−1≤t≤0
so a piecewise parametrización de esta ruta es:
\ (\ vecs r (t) =\ begin {cases}
t\,\ hat {\ mathbf {i}} +\ sqrt [3] {t}\,\ hat {\ mathbf {j}}, & 0\ le t\ le 1\\\ left (2-t\ right)\,\ hat {
\ mathbf {i}} +\ left (2-t\ right)\,\ hat {\ mathbf {i} +\ left (2-t\ right)\ t\ derecha) ^4\,\ hat {\ mathbf {j}}, & 1\ lt t\ le 2
\ end {casos}\)
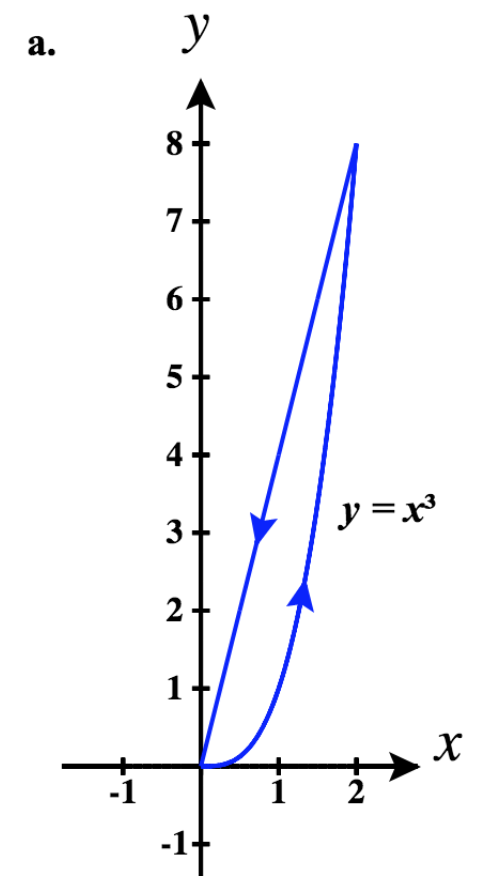
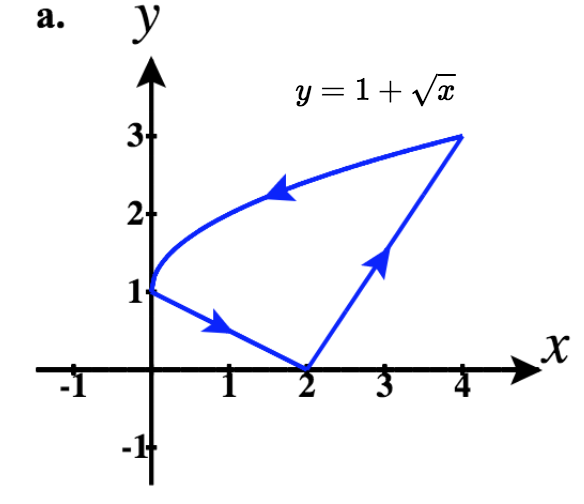
42)
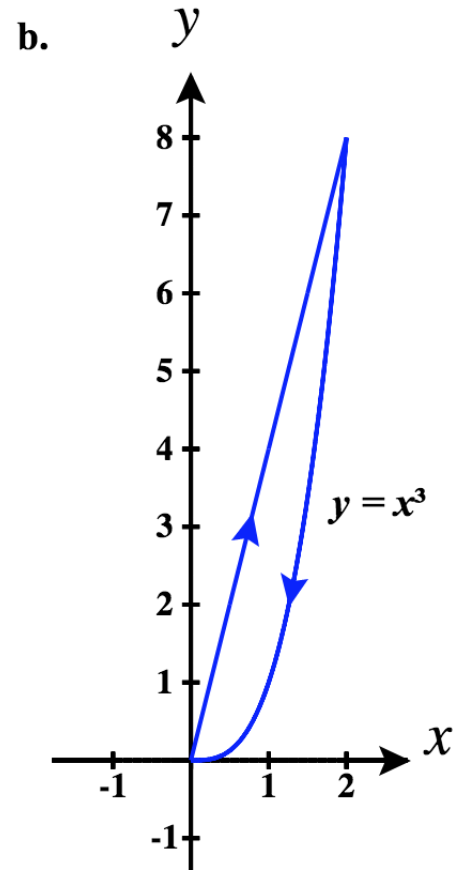
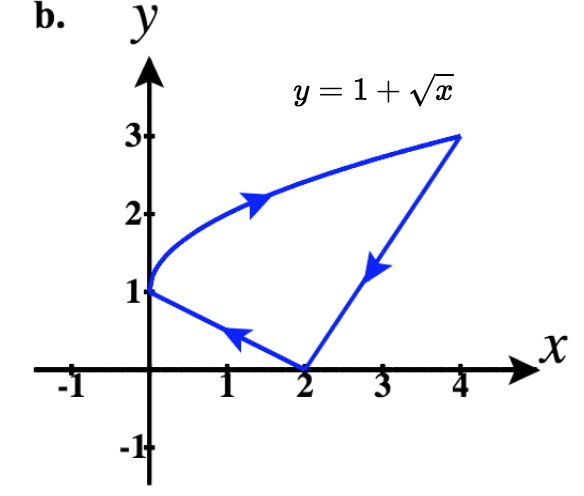
43)
- Contestar
- a.⇀r1(t)=tˆi+0ˆj for for0≤t≤2
⇀r2(t)=−tˆi+(2+t)ˆj−2≤t≤−1
⇀r3(t)=−tˆi+(−t)3ˆj for−1≤t≤0
Así que una parametrización por partes de esta ruta es:
\ (\ vecs r (t) =\ begin {cases}
t\,\ hat {\ mathbf {i}}, & 0\ le t\ le 2\\
\ izquierda (4-t\ derecha)\,\ hat {\ mathbf {i}} +\ izquierda (t-2\ derecha)\,\ hat {\ mathbf {j}}, & 2\ lt t\ le 3\
\ izquierda (4-t\ derecha)\,\ hat {\ mathbf {i}} +\ izquierda (4-t\ derecha) ^3\,\ sombrero {\ mathbf {j}}, & 3\ lt t\ le 4
\ end {casos}\)
b.⇀r1(t)=tˆi+t3ˆj for0≤t≤1
⇀r2(t)=tˆi+(2−t)ˆj for1≤t≤2
⇀r3(t)=−tˆi+0ˆj for−2≤t≤0
Así que una parametrización por partes de esta ruta es:
\ (\ vecs r (t) =\ begin {cases}
t\,\ hat {\ mathbf {i}} + t^3\,\ hat {\ mathbf {j}}, & 0\ le t\ le 1\\
t\,\ hat {\ mathbf {i}} +\ izquierda (2 - t\ derecha)\,\ hat {\ mathbf {j}}, & 1\ lt t\ le 2\\ izquierda (4-t
\ derecha)\,\ hat {\ mathbf {j} bf {i}}, & 2\ lt t\ le 4
\ fin {casos}\)
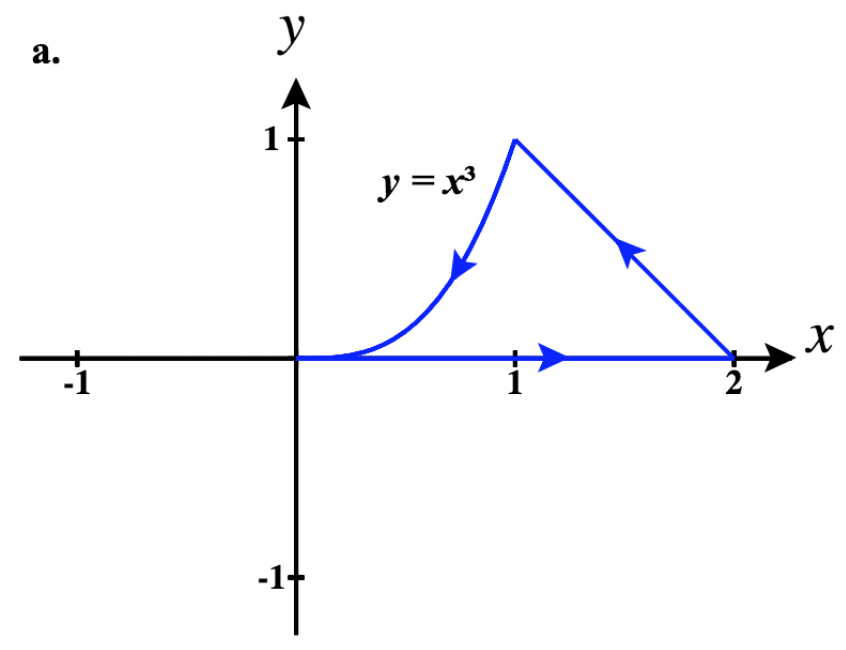
44)
Preguntas adicionales sobre funciones valoradas por vectores
Para las preguntas 45 a 48, considere la curva descrita por la función vectorizada⇀r(t)=(50e−tcost)ˆi+(50e−tsint)ˆj+(5−5e−t)ˆk.
45) ¿A qué corresponde el punto inicial del camino⇀r(0)?
- Contestar
- (50,0,0)
46) ¿Qué eslimt→∞⇀r(t)?
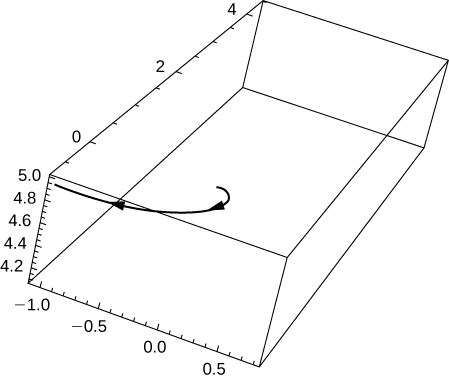
47) [T] Utilice la tecnología para bosquejar la curva.
- Contestar
48) Eliminar el parámetro t para mostrar quez=5−r10 donder2=x2+y2.
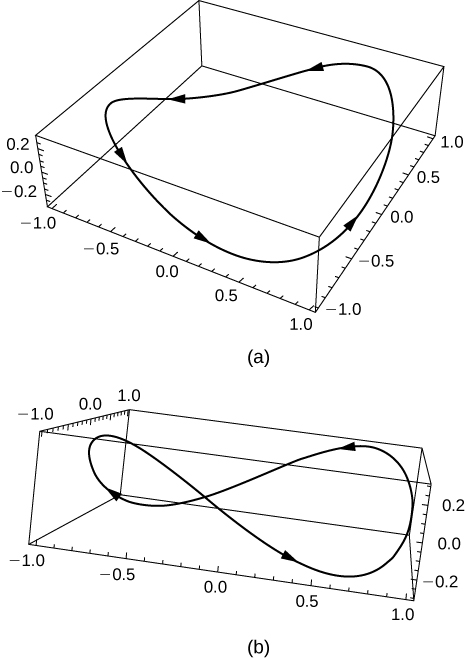
49) [T] Vamos⇀r(t)=costˆi+sintˆj+0.3sin(2t)ˆk. Utilice la tecnología para graficar la curva (llamada curva de montaña rusa) a lo largo del intervalo[0,2π). Elija al menos dos vistas para determinar los picos y valles.
- Contestar
50) [T] Utilice el resultado del problema anterior para construir una ecuación de una montaña rusa con una caída pronunciada desde el pico e inclinación pronunciada desde el “valle”. Entonces, usa la tecnología para graficar la ecuación.
51) Utilizar los resultados de los dos problemas anteriores para construir una ecuación de un camino de una montaña rusa con más de dos puntos de inflexión (picos y valles).
- Contestar
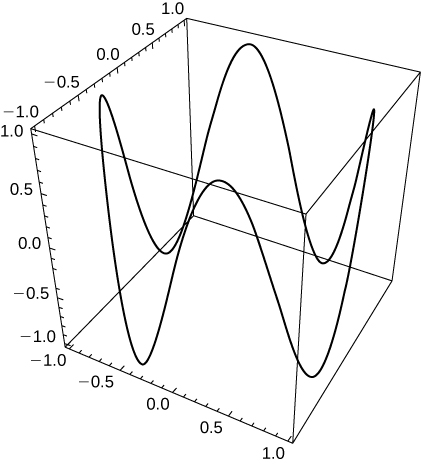
-
Una posibilidad es⇀r(t)=costˆi+sintˆj+sin(4t)ˆk. Al aumentar el coeficiente det en el tercer componente, aumentará el número de puntos de inflexión.
52) Completar la siguiente investigación.
- Grafica la curva⇀r(t)=(4+cos(18t))cos(t)ˆi+(4+cos(18t)sin(t))ˆj+0.3sin(18t)ˆk usando dos ángulos de visión de tu elección para ver la forma general de la curva.
- ¿La curva se parece a un “slinky”?
- ¿Qué cambios se deben hacer en la ecuación para aumentar el número de bobinas del slinky?
Colaboradores
Paul Seeburger (Monroe Community College) creó los problemas 12, 14, 19, 22, 30-33, 37- 44.