13.5: Capítulo 13 Ejercicios de revisión
( \newcommand{\kernel}{\mathrm{null}\,}\)
¿Verdadero o Falso? Justifica tu respuesta con una prueba o un contraejemplo.
1. Una ecuación paramétrica que pasa por puntosP yQ puede ser dada por\vecs r(t)=⟨t^2,\, 3t+1,\, t−2⟩, dóndeP(1,4,−1) yQ(16,11,2).
2. \dfrac{d}{dt}\Big[\vecs u(t)×\vecs u(t)\Big]=2\vecs u′(t)×\vecs u(t)
- Responder
- Falso,\dfrac{d}{dt}\Big[\vecs u(t)×\vecs u(t)\Big]=\vecs 0.
3. La curvatura de un círculo de radior es constante en todas partes. Además, la curvatura es igual a1/r.
4. La velocidad de una partícula con una función de posición\vecs r(t) es\dfrac{\vecs r′(t)}{\|\vecs r′(t)\|}.
- Responder
- Falso, es\|\vecs r′(t)\|
Encuentra los dominios de las funciones vectoriales.
5. \vecs r(t)=⟨\sin(t),\, \ln(t),\, \sqrt{t}⟩
6. \vecs r(t)=\left\langle e^t,\,\dfrac{1}{\sqrt{4−t}},\,\sec t\right\rangle
- Responder
- t<4, \; t≠\dfrac{nπ}{2}
Esboce las curvas para las siguientes ecuaciones vectoriales. Use una calculadora si es necesario.
7. [T]\vecs r(t)=⟨t^2,\, t^3⟩
8. [T]\vecs r(t)=⟨\sin(20t)e^{−t}, \, \cos(20t)e^{−t}, \, e^{−t}⟩
- Responder
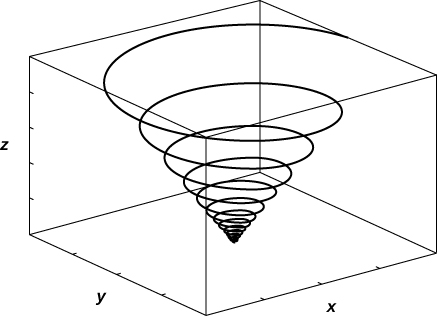
Encuentre una función vectorial que describa las siguientes curvas.
9. Intersección del cilindrox^2+y^2=4 con el planox+z=6
10. Intersección del conoz=\sqrt{x^2+y^2} y el planoz=y−4
- Responder
- \vecs r(t)=\left\langle t, \, 2-\frac{t^2}{8},\, -2 - \frac{t^2}{8}\right\rangle
Encuentra las derivadas de\vecs u(t), \, \vecs u′(t), \, \vecs u′(t)×\vecs u(t), \, \vecs u(t)×\vecs u′(t), y\vecs u(t)·\vecs u′(t). Encuentra el vector tangente unitario.
11. \vecs u(t)=⟨e^t, \, e^{−t}⟩
12. \vecs u(t)=⟨t^2,\, 2t+6, \, 4t^5−12⟩
- Responder
- \vecs u′(t)=⟨2t, \, 2, \, 20t^4⟩,
\vecs u″(t)=⟨2, \, 0, \, 80t^3⟩,
\dfrac{d}{dt}\Big[\vecs u′(t)×\vecs u(t)\Big]=⟨−480t^3−160t^4, \, 24+75t^2, \, 12+4t⟩,
\dfrac{d}{dt}\Big[\vecs u(t)×\vecs u′(t)\Big]=⟨480t^3+160t^4, \, -24-75t^2, \, -12-4t⟩,
\dfrac{d}{dt}\Big[\vecs u(t)⋅\vecs u′(t)\Big]=720t^8−9600t^3+6t^2+4,
vector tangente unitario:\vecs T(t)=\dfrac{2t}{\sqrt{400t^8+4t^2+4}}\,\mathbf{\hat i}+\dfrac{2}{\sqrt{400t^8+4t^2+4}}\,\mathbf{\hat j}+\dfrac{20t^4}{\sqrt{400t^8+4t^2+4}}\,\mathbf{\hat k}
Evaluar las siguientes integrales.
13. \displaystyle ∫\left(\tan(t)\sec(t)\,\mathbf{\hat i}−te^{3t}\,\mathbf{\hat j}\right)\, dt
14. \displaystyle ∫_1^4 \vecs u(t) \, dt,con\vecs u(t)=\left\langle\dfrac{\ln t}{t}, \, \dfrac{1}{\sqrt{t}}, \, \sin\left(\frac{tπ}{4}\right)\right\rangle
- Responder
- \dfrac{\ln(4^2)}{2}\,\mathbf{\hat i}+2\,\mathbf{\hat j}+\dfrac{2(2+\sqrt{2})}{\pi}\,\mathbf{\hat k}
Encuentra la longitud para las siguientes curvas.
15. \vecs r(t)=⟨3t,\, 4\cos t, \, 4\sin t ⟩para1≤t≤4
16. \vecs r(t)=2\,\mathbf{\hat i}+t\,\mathbf{\hat j}+3t^2\,\mathbf{\hat k}para0≤t≤1
- Responder
- \dfrac{\sqrt{37}}{2}+\frac{1}{12}\sinh^{−1} 6
Reparameterizar las siguientes funciones con respecto a su longitud de arco medida desdet=0 la dirección de aumentot.
17. \vecs r(t)=2t\,\mathbf{\hat i}+(4t−5)\,\mathbf{\hat j}+(1−3t)\,\mathbf{\hat k}
18. \vecs r(t)=\cos(2t)\,\mathbf{\hat i}+8t\,\mathbf{\hat j}−\sin(2t)\,\mathbf{\hat k}
- Responder
- \vecs r(t(s))=\cos\left(\frac{2s}{\sqrt{65}}\right)\,\mathbf{\hat i}+\frac{8s}{\sqrt{65}}\,\mathbf{\hat j}−\sin\left(\frac{2s}{\sqrt{65}}\right)\,\mathbf{\hat k}
Encuentra la curvatura para las siguientes funciones vectoriales.
19. \vecs r(t)=(2\sin t)\,\mathbf{\hat i}−4t\,\mathbf{\hat j}+(2\cos t)\,\mathbf{\hat k}
20. \vecs r(t)=\sqrt{2}e^t\,\mathbf{\hat i}+\sqrt{2}e^{−t}\,\mathbf{\hat j}+2t\,\mathbf{\hat k}
- Responder
- \dfrac{e^{2t}}{\left(e^{2t}+1\right)^2}
21. Encuentre el vector tangente unitario, el vector normal unitario y el vector binormal para\vecs r(t)=2\cos t\,\mathbf{\hat i} +3t\,\mathbf{\hat j}+2sint\,\mathbf{\hat k}.
22. Encuentra los componentes de aceleración tangencial y normal con el vector de posición\vecs r(t)=⟨\cos t,\, \sin t, \, e^t⟩.
- Contestar
- a_T=\dfrac{e^{2t}}{1+e^{2t}},
a_N=\dfrac{\sqrt{2e^{2t}+4e^{2t}\sin t\cos t+1}}{1+e^{2t}}
23. Un carro de la noria se mueve a una velocidad constantev y tiene un radio constanter. Encuentra la aceleración tangencial y normal del carro de la noria.
24. La posición de una partícula viene dada por\vecs r(t)=⟨t^2, \, \ln t, \, \sin(πt)⟩, dondet se mide en segundos yr se mide en metros. Encuentre las funciones de velocidad, aceleración y velocidad. ¿Cuál es la posición, velocidad, velocidad y aceleración de la partícula a 1 seg?
- Contestar
- \vecs v(t)=\left\langle 2t,\, \frac{1}{t}, \, \pi\cos(πt)\right\rangle\text{ m/sec},
\vecs a(t)=\left\langle 2, \, −\frac{1}{t^2}, \, −\pi^2\sin(πt) \right\rangle\text{ m/sec}^2,
\text{speed}(t)=\sqrt{4t^2+\frac{1}{t^2}+\pi^2\cos^2(πt)}\text{ m/sec};
At=1,\; \vecs r(1)=⟨1,0,0⟩ m,\vecs v(1)=⟨2,−1,\pi⟩ m/seg,\vecs a(1)=⟨2,−1,0⟩ m/seg 2 y\text{speed}(1) =\sqrt{5+\pi^2} m/seg
Los siguientes problemas consideran lanzar una bala de cañón desde un cañón. La bala de cañón se dispara fuera del cañón con un ánguloθ y una velocidad inicial\vecs v_0. La única fuerza que actúa sobre la bala de cañón es la gravedad, por lo que comenzamos con una aceleración constante\vecs a(t)=−g\,\mathbf{\hat j}.
25. Encuentra la función de vector de velocidad\vecs v(t).
26. Encuentra el vector de posición\vecs r(t) y la representación paramétrica para la posición.
- Contestar
- \vecs r(t)=\vecs v_0t−\dfrac{gt^2}{2}\,\mathbf{\hat j},
\vecs r(t)=⟨v_0(\cos θ)t,\,v_0(\sin θ)t,−\dfrac{gt^2}{2}⟩dondev_0 = \|\vecs v_0\|.
27. ¿En qué ángulo necesitas disparar la bala de cañón para que la distancia horizontal sea mayor? ¿Cuál es la distancia total que recorrería?


