14.3E: Ejercicios para la Sección 14.3

En el siguiente ejercicio, calcule la derivada parcial utilizando únicamente las definiciones de límite.

1)\(\dfrac{∂z}{∂y}\) para\( z=x^2−3xy+y^2\)

Contestar

\(\dfrac{∂z}{∂y}=−3x+2y\)

Para los ejercicios 2 - 5, calcule el signo de la derivada parcial utilizando la gráfica de la superficie.

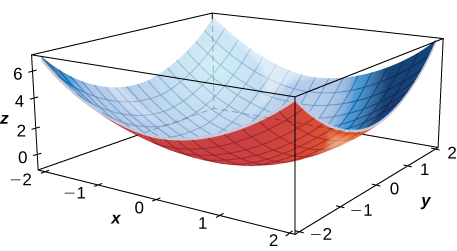
2)\( f_x(1,1)\)

3)\( f_x(−1,1)\)

Contestar

El signo es negativo.

4)\( f_y(1,1)\)

5)\( f_x(0,0)\)

Contestar

La derivada parcial es cero en el origen.

En los ejercicios 6 - 16, calcular las derivadas parciales solicitadas.

6)\( \dfrac{∂z}{∂x}\) para\( z=\sin(3x)\cos(3y)\)

7)\( \dfrac{∂z}{∂y}\) para\( z=\sin(3x)\cos(3y)\)

Contestar

\( \dfrac{∂z}{∂y}=−3\sin(3x)\sin(3y)\)

8)\( \dfrac{∂z}{∂x}\) y\( \dfrac{∂z}{∂y}\) para\( z=x^8e^3y\)

9)\( \dfrac{∂z}{∂x}\) y\( \dfrac{∂z}{∂y}\) para\( z=\ln(x^6+y^4)\)

Contestar

\( \dfrac{∂z}{∂x}=\frac{6x^5}{x^6+y^4};\quad \dfrac{∂z}{∂y}=\frac{4y^3}{x^6+y^4}\)

10)\( f_y(x,y)\) Buscar\( f(x,y)=e^{xy}\cos(x)\sin(y).\)

11) Let\( z=e^{xy}.\) Find\( \dfrac{∂z}{∂x}\) y\( \dfrac{∂z}{∂y}\).

Contestar

\( \dfrac{∂z}{∂x}=ye^{xy};\quad \dfrac{∂z}{∂y}=xe^{xy}\)

12) Vamos\( z=\ln(\frac{x}{y})\). Encontrar\( \dfrac{∂z}{∂x}\) y\( \dfrac{∂z}{∂y}\).

13) Let\( z=\tan(2x−y).\) Find\( \dfrac{∂z}{∂x}\) y\( \dfrac{∂z}{∂y}\).

Contestar

\( \dfrac{∂z}{∂x}=2\sec^2(2x−y),\quad \dfrac{∂z}{∂y}=−\sec^2(2x−y)\)

14) Let\( z=\sinh(2x+3y).\) Find\( \dfrac{∂z}{∂x}\) y\( \dfrac{∂z}{∂y}\).

15) Dejar\( f(x,y)=\arctan(\frac{y}{x}).\) Evaluar\( f_x(2,−2)\) y\( f_y(2,−2)\).

Contestar

\( f_x(2,−2)=\frac{1}{4}=f_y(2,−2)\)

16) Let\( f(x,y)=\dfrac{xy}{x−y}.\) Find\( f_x(2,−2)\) y\( f_y(2,−2).\)

17) Encontrar\( \dfrac{∂z}{∂x}\) en\( (0,1)\) para\( z=e^{−x}cos(y)\).

Contestar

\( \dfrac{∂z}{∂x}=−\cos(1)\)

18) Dado\( f(x,y,z)=x^3yz^2,\) hallazgo\( \dfrac{∂^2f}{∂x∂y}\) y\( f_z(1,1,1).\)

19) Dado\( f(x,y,z)=2\sin(x+y),\) hallazgo\( f_x(0,\frac{π}{2},−4)\),\(f_y(0,\frac{π}{2},−4)\), y\( f_z(0,\frac{π}{2},−4)\).

Contestar

\( f_x(x,y,z)=0,\quad f_y(x,y,z)=0,\quad f_z(x,y,z)=0\)

20) El área de un paralelogramo con longitudes laterales adyacentes que son\( a\) y\( b\), y en la que se encuentra el ángulo entre estos dos lados\( θ\), viene dada por la función\( A(a,b,θ)=ba\sin(θ).\) Encontrar la tasa de cambio del área del paralelogramo con respecto a lo siguiente:

a. Lado\(a\)

b. Lateral\(b\)

c. Ángulo\(θ\)

21) Expresar el volumen de un cilindro circular derecho en función de dos variables:

a. su radio\( r\) y su altura\( h\).

b. Demostrar que la tasa de cambio del volumen del cilindro con respecto a su radio es el producto de su circunferencia multiplicado por su altura.

c. Demostrar que la tasa de cambio del volumen del cilindro con respecto a su altura es igual al área de la base circular.

Contestar

\( a. V(r,h)=πr^2h\)
\( b. \dfrac{∂V}{∂r}=2πrh\)
\( c. \dfrac{∂V}{∂h}=πr^2\)

22) Calcular\( \dfrac{∂w}{∂z}\) para\( w=z\sin(xy^2+2z).\)

En los ejercicios 23 - 39, encuentra las derivadas parciales de orden superior indicadas.

23)\( f_{xy}(x,y)\) para\( f(x,y)=\ln(x−y)\)

Contestar

\( f_{xy}(x,y)=\frac{1}{(x−y)^2}\)

24)\( f_{yx}(x,y)\) para\( f(x, y)=\ln(x−y)\)

25) Let\( z=x^2+3xy+2y^2.\) Find\( \dfrac{∂^2z}{∂x^2}\) y\( \dfrac{∂^2z}{∂y^2}\).

Contestar

\( \dfrac{∂^2z}{∂x^2}=2,\quad \dfrac{∂^2z}{∂y^2}=4\)

26) Dado\( z=e^x\tan y\), encontrar\( \dfrac{∂^2z}{∂x∂y}\) y\( \dfrac{∂^2z}{∂y∂x}\).

27) Dado\( f(x,y,z)=xyz,\) hallazgo\( f_{xyy}(x,y,z),\, f_{yxy}(x,y,z),\) y\( f_{yyx}(x,y,z)\).

Contestar

\( f_{xyy}(x,y,z)=f_{yxy}(x,y,z)=f_{yyx}(x,y,z)=0\)

28) Dado\( f(x,y,z)=e^{−2x}\sin(z^2y),\) demostrar que\( f_{xyy}(x,y,z)=f_{yxy}(x,y,z)\).

29) Mostrar que\( z=\frac{1}{2}(e^y−e^{−y})\sin x\) es una solución de la ecuación diferencial\( \dfrac{∂^2z}{∂x^2}+\dfrac{∂^2z}{∂y^2}=0.\)

Contestar

\( \dfrac{d^2z}{dx^2}=−\frac{1}{2}(e^y−e^{−y})\sin x\)
\( \dfrac{d^2z}{dy^2}=\frac{1}{2}(e^y−e^{−y})\sin x\)
\( \dfrac{d^2z}{dx^2}+\dfrac{d^2z}{dy^2}=0\)

30)\( f_{xx}(x,y)\) Buscar\( f(x,y)=\frac{4x^2}{y}+\frac{y^2}{2x}.\)

31) Let\( f(x,y,z)=x^2y^3z−3xy^2z^3+5x^2z−y^3z.\) Find\( f_{xyz}.\)

Contestar

\( f_{xyz}(x,y,z)=6y^2x−18yz^2\)

32) Vamos a\( F(x,y,z)=x^3yz^2−2x^2yz+3xz−2y^3z.\) encontrar\( F_{xyz}(x,y,z)\).

33) Dado\( f(x,y)=x^2+x−3xy+y^3−5,\) encontrar todos los puntos en los que\( f_x(x,y)=f_y(x,y)=0\) simultáneamente.

Contestar

\( (\frac{1}{4},\frac{1}{2}),\quad (1,1)\)

34) Dado\( f(x,y)=2x^2+2xy+y^2+2x−3,\) encontrar todos los puntos en los que\( \dfrac{∂f}{∂x}=0\) y\( \dfrac{∂f}{∂y}=0\) simultáneamente.

35) Dado\( f(x,y)=y^3−3yx^2−3y^2−3x^2+1\), encontrar todos los puntos\( f\) en los que\( f_x(x, y)=f_y(x, y)=0\) simultáneamente.

Contestar

\( (0,0),\quad (0,2),\quad (\sqrt{3},−1), \quad (−\sqrt{3},−1)\)

36) Dado\( f(x,y)=15x^3−3xy+15y^3,\) encontrar todos los puntos en los que\( f_x(x,y)=f_y(x,y)=0\) simultáneamente.

37) Demostrar que\( z=e^x\sin y\) satisface la ecuación\( \dfrac{∂^2z}{∂x^2}+\dfrac{∂^2z}{∂y^2}=0.\)

Contestar

\( \dfrac{∂^2z}{∂x^2}+\dfrac{∂^2z}{∂y^2}=e^x\sin y−e^x\sin y=0\)

38) Demostrar que\( f(x,y)=\ln(x^2+y^2)\) resuelve la ecuación de Laplace\( \dfrac{∂^2z}{∂x^2}+\dfrac{∂^2z}{∂y^2}=0.\)

39) Demostrar que\( z=e^{−t}\cos(\frac{x}{c})\) satisface la ecuación de calor\( \dfrac{∂z}{∂t}=−e^{−t}\cos(\frac{x}{c}).\)

Contestar

\( c^2\dfrac{∂^2z}{∂x^2}=e^{−t}\cos(\frac{x}{c})\)

40)\(\displaystyle \lim_{Δx→0}\frac{f(x+Δx)−f(x,y)}{Δx}\) Buscar\( f(x,y)=−7x−2xy+7y.\)

41)\(\displaystyle \lim_{Δy→0}\frac{f(x,y+Δy)−f(x,y)}{Δy}\) Buscar\( f(x,y)=−7x−2xy+7y.\)

Contestar

\( \dfrac{∂f}{∂y}=−2x+7\)

42)\(\displaystyle \lim_{Δx→0}\frac{Δf}{Δx}=\lim_{Δx→0}\frac{f(x+Δx,y)−f(x,y)}{Δx}\) Buscar\( f(x,y)=x^2y^2+xy+y.\)

43)\(\displaystyle \lim_{Δx→0}\frac{Δf}{Δx}=\lim_{Δx→0}\frac{f(x+Δx,y)−f(x,y)}{Δx}\) Buscar\( f(x,y)=\sin(xy).\)

Contestar

\( \dfrac{∂f}{∂x}=y\cos xy\)

44) La función\( P(T,V)=\dfrac{nRT}{V}\) da la presión en un punto en un gas en función de la temperatura\( T\) y el volumen\( V\). Las letras\( n\) y\( R\) son constantes. Encontrar\( \dfrac{∂P}{∂V}\) y\( \dfrac{∂P}{∂T}\), y explicar lo que representan estas cantidades.

45) La ecuación para el flujo de calor en el\( xy\) plano es\( \dfrac{∂f}{∂t}=\dfrac{∂^2f}{∂x^2}+\dfrac{∂^2f}{∂y^2}\). Demostrar que\( f(x,y,t)=e^{−2t}\sin x\sin y\) es una solución.

46) La ecuación básica de onda es\( f_{tt}=f_{xx}.\) Verificar que\( f(x,t)=\sin(x+t)\) y\( f(x,t)=\sin(x−t)\) son soluciones.

47) La ley de los cosenos puede pensarse como una función de tres variables. Dejar\( x,y,\) y\( θ\) ser dos lados de cualquier triángulo donde el ángulo\( θ\) es el ángulo incluido entre los dos lados. Entonces,\( F(x,y,θ)=x^2+y^2−2xy\cos θ\) da el cuadrado del tercer lado del triángulo. Buscar\( \dfrac{∂F}{∂θ}\) y\( \dfrac{∂F}{∂x}\) cuándo\( x=2,\,y=3,\) y\( θ=\frac{π}{6}.\)

Contestar

\( \dfrac{∂F}{∂θ}=6,\quad \dfrac{∂F}{∂x}=4−3\sqrt{3}\)

48) Supongamos que los lados de un rectángulo están cambiando con respecto al tiempo. El primer lado está cambiando a un ritmo de\( 2\) in. /seg mientras que el segundo lado está cambiando a la velocidad de\( 4\) en/seg. ¿Qué tan rápido cambia la diagonal del rectángulo cuando el primer lado mide\( 16\) pulg. y el segundo lado mide\( 20\) en.? (Redondear la respuesta a tres decimales.)

49) Una función de producción Cobb-Douglas es\( f(x,y)=200x^{0.7}y^{0.3},\) donde\( x\) y\( y\) representan la cantidad de mano de obra y capital disponible. Let\( x=500\) y\( y=1000.\) Find\( \dfrac{∂f}{∂x}\) y\( \dfrac{∂f}{∂y}\) a estos valores, que representan la productividad marginal del trabajo y del capital, respectivamente.

Contestar

\( \dfrac{∂f}{∂x}\)\( (500,1000)=172.36, \quad \dfrac{∂f}{∂y}\)en\( (500,1000)=36.93\)

50) El índice de temperatura aparente es una medida de cómo se siente la temperatura, y se basa en dos variables:\( h\), que es la humedad relativa, y\( t\), que es la temperatura del aire.

\( A=0.885t−22.4h+1.20th−0.544.\)Buscar\( \dfrac{∂A}{∂t}\) y\( \dfrac{∂A}{∂h}\) cuándo\( t=20°F\) y\( h=0.90.\)