16.4: Teorema de Green
- Page ID
- 116753
- Aplicar la forma de circulación del teorema de Green.
- Aplicar la forma de flujo del teorema de Green.
- Calcular la circulación y el flujo en regiones más generales.
En esta sección, examinamos el teorema de Green, que es una extensión del Teorema Fundamental del Cálculo a dos dimensiones. El teorema de Green tiene dos formas: una forma de circulación y una forma de flujo, las cuales requieren que la región\(D\) en la doble integral esté simplemente conectada. No obstante, extenderemos el teorema de Green a regiones que no están simplemente conectadas.
En pocas palabras, el teorema de Green relaciona una línea integral alrededor de una curva plana simplemente cerrada\(C\) y una doble integral sobre la región encerrada por\(C\). El teorema es útil porque nos permite traducir integrales de línea difíciles en integrales dobles más simples, o integrales dobles difíciles en integrales de línea más simples.
Extendiendo el Teorema Fundamental del Cálculo
Recordemos que el Teorema Fundamental del Cálculo dice que
\[\int_a^b F′(x)\,dx=F(b)−F(a). \nonumber \]
Como declaración geométrica, esta ecuación dice que la integral sobre la región debajo de la gráfica de\(F′(x)\) y por encima del segmento de línea\([a,b]\) depende únicamente del valor de\(F\) en los puntos finales\(a\) y\(b\) de ese segmento. Dado que los números\(a\) y\(b\) son el límite del segmento de línea\([a,b]\), el teorema dice que podemos calcular integral con\(\int_a^b F′(x)\,dx\) base en información sobre el límite del segmento de línea\([a,b]\) (Figura\(\PageIndex{1}\)). La misma idea es cierta del Teorema Fundamental para Integrales de Línea:
\[\int_C \vecs \nabla f·d\vecs r=f(\vecs r(b))−f(\vecs r(a)). \nonumber \]
Cuando tenemos una función potencial (una “antiderivada”), podemos calcular la integral de línea basándose únicamente en información sobre el límite de la curva\(C\).
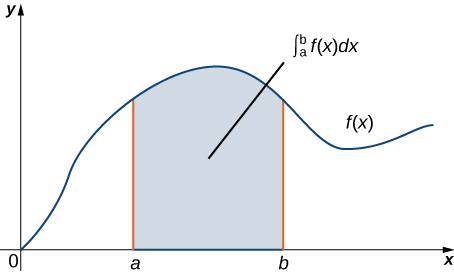
El teorema de Green toma esta idea y la extiende al cálculo de dobles integrales. El teorema de Green dice que podemos calcular una doble integral sobre región con\(D\) base únicamente en información sobre el límite de\(D\). El teorema de Green también dice que podemos calcular una línea integral sobre una simple curva cerrada\(C\) basada únicamente en información sobre la región que lo\(C\) encierra. En particular, el teorema de Green conecta una doble integral sobre región\(D\) con una línea integral alrededor del límite de\(D\).
Forma de circulación del teorema de Green
La primera forma del teorema de Green que examinamos es la forma de circulación. Esta forma del teorema relaciona la integral de la línea vectorial sobre una curva plana simple y cerrada\(C\) con una doble integral sobre la región encerrada por\(C\). Por lo tanto, la circulación de un campo vectorial a lo largo de una curva cerrada simple se puede transformar en una doble integral y viceversa.
Let\(D\) Ser una región abierta, simplemente conectada con una curva límite\(C\) que es una curva cerrada simple y lisa por tramos orientada en sentido antihorario (Figura\(\PageIndex{1}\)). Let\(\vecs F=⟨P,Q⟩\) Ser un campo vectorial con funciones componentes que tienen derivadas parciales continuas encendidas\(D\). Entonces,
\[ \begin{align} \oint_C \vecs F·d\vecs r =\oint_C P\,dx+Q\,dy \\[4pt] =\iint_D (Q_x−P_y)\,dA. \end{align} \nonumber \]
Observe que el teorema de Green solo se puede usar para un campo vectorial bidimensional\(\vecs F\). Si\(\vecs F\) es un campo tridimensional, entonces el teorema de Green no aplica. Desde
\[\displaystyle \int_C P\,dx+Q\,dy=\int_C \vecs F·\vecs T\,ds \nonumber \]
esta versión del teorema de Green es a veces referida como la forma tangencial del teorema de Green.
La prueba del teorema de Green es más bien técnica, y más allá del alcance de este texto. Aquí examinamos una prueba del teorema en el caso especial que\(D\) es un rectángulo. Por ahora, observe que podemos confirmar rápidamente que el teorema es cierto para el caso especial en el que\(\vecs F=⟨P,Q⟩\) es conservador. En este caso,
\[\oint_C P\,dx+Q\,dy=0 \nonumber \]
porque la circulación es cero en campos vectoriales conservadores. \(\vecs F\)satisface la condición transversal parcial, por lo que\(P_y=Q_x\). Por lo tanto,
\[\iint_D (Q_x−P_y)\,dA=\int_D 0\,dA=0=\oint_C P\,dx+Q\,dy \nonumber \]
lo que confirma el teorema de Green en el caso de los campos vectoriales conservadores.
Ahora probemos que la forma de circulación del teorema de Green es cierta cuando la región\(D\) es un rectángulo. Dejar\(D\) ser el rectángulo\([a,b]×[c,d]\) orientado en sentido antihorario. Luego, el límite\(C\) de\(D\) consta de cuatro piezas lisas por partes\(C_1\)\(C_2\),\(C_3\), y\(C_4\) (Figura\(\PageIndex{3}\)). Parametrizamos cada lado de la\(D\) siguiente manera:
\(C_1: \vecs r_1(t)=⟨t,c⟩\),\(a≤t≤b\)
\(C_2: \vecs r_2(t)=⟨b,t⟩\),\(c≤t≤d\)
\(−C_3: \vecs r_3(t)=⟨t,d⟩\),\(a≤t≤b\)
\(−C_4: \vecs r_4(t)=⟨a,t⟩\),\(c≤t≤d\).
Entonces,
\[\begin{align*} \int_C \vecs F·d \vecs r &=\int_{C_1} \vecs F·d \vecs r+\int_{C_2} \vecs F·d \vecs r+\int_{C_3} \vecs F·d \vecs r+\int_{C_4} \vecs F·d \vecs r \\[4pt] &=\int_{C_1} \vecs F·d \vecs r+\int_{C_2} \vecs F·d \vecs r−\int_{−C_3} \vecs F·d \vecs r−\int_{−C_4} \vecs F·d \vecs r \\[4pt] &=\int_a^b \vecs F( \vecs r_1(t))· \vecs r_1'(t)\,dt+\int_c^d \vecs F( \vecs r_2(t))· \vecs r_2'(t)\,dt−\int_a^b \vecs F( \vecs r_3(t))· \vecs r_3'(t)\,dt−\int_c^d \vecs F( \vecs r_4(t))·\vecs r_4'(t)\,dt\\[4pt] &=\int_a^b P(t,c)\,dt+\int_c^dQ(b,t)\,dt−\int_a^bP(t,d)\,dt−\int_c^dQ(a,t)\,dt \\[4pt] &=\int_a^b(P(t,c)−P(t,d))\,dt+\int_c^d(Q(b,t)−Q(a,t))\,dt\\[4pt] &=−\int_a^b(P(t,d)−P(t,c))\,dt+\int_c^d(Q(b,t)−Q(a,t))\,dt. \end{align*}\]
Por el Teorema Fundamental del Cálculo,
\[P(t,d)−P(t,c)=\int_c^d \dfrac{\partial}{\partial y}P(t,y)dy \nonumber \]
y
\[Q(b,t)−Q(a,t)=\int_a^b \dfrac{\partial}{\partial x} Q(x,t)\,dx. \nonumber \]
Por lo tanto,
\[−\int_a^b(P(t,d)−P(t,c))\,dt+\int_c^d(Q(b,t)−Q(a,t))\,dt=−\int_a^b\int_c^d \dfrac{\partial}{\partial y} P(t,y)\,dy\,dt+\int_c^d\int_a^b \dfrac{\partial}{\partial x}Q(x,t)\,dx\,dt. \nonumber \]
Pero,
\[\begin{align*} −\int_a^b\int_c^d \dfrac{\partial}{\partial y}P(t,y)\,dy\,dt+\int_c^d\int_a^b \dfrac{\partial}{\partial x}Q(x,t)\,dx\,dt &=−\int_a^b\int_c^d \dfrac{\partial}{\partial y}P(x,y)\,dy\,dx+\int_c^d\int_a^b \dfrac{\partial}{\partial x}Q(x,y)\,dx\,dy \\[4pt] &=\int_a^b\int_c^d(Q_x−P_y)\,dy\,dx\\[4pt] &=\iint_D(Q_x−P_y)\,dA. \end{align*}\]
Por lo tanto,\(\displaystyle \int_C \vecs F\cdot d\vecs r=\iint_D(Q_x−P_y)\,dA\) y hemos probado el teorema de Green en el caso de un rectángulo.
\(\square\)
Para probar el teorema de Green sobre una región general\(D\), podemos descomponernos\(D\) en muchos rectángulos diminutos y usar la prueba de que el teorema funciona sobre rectángulos. Los detalles son técnicos, sin embargo, y más allá del alcance de este texto.
Calcular la integral de línea
\[\oint_C x^2ydx+(y−3)dy, \nonumber \]
donde\(C\) es un rectángulo con vértices\((1,1)\),\((4,1)\)\((4,5)\), y\((1,5)\) orientado en sentido antihorario.
Solución
Vamos\( \vecs F(x,y)=⟨P(x,y),Q(x,y)⟩=⟨x^2y,y−3⟩\). Entonces,\(Q_x(x,y)=0\) y\(P_y(x,y)=x^2\). Por lo tanto,\(Q_x−P_y=−x^2\).
Dejar\(D\) ser la región rectangular encerrada por\(C\) (Figura\(\PageIndex{4}\)). Por el teorema de Green,
\[\begin{align*} \oint_C x^2ydx+(y−3)\,dy &=\iint_D (Q_x−P_y)\,dA \\[4pt] &=\iint_D −x^2 \,dA=\int_1^5\int_1^4−x^2\,dx\,dy \\[4pt] &=\int_1^5−21\,dy=−84.\end{align*}\]
Análisis
Si tuviéramos que evaluar esta integral de línea sin usar el teorema de Green, necesitaríamos parametrizar cada lado del rectángulo, dividir la integral de línea en cuatro integrales de línea separadas y usar los métodos de la sección titulada Integrales de línea para evaluar cada integral. Además, dado que el campo vectorial aquí no es conservador, no podemos aplicar el Teorema Fundamental para Integrales de Línea. El teorema de Green simplifica mucho el cálculo.
Calcular el trabajo realizado sobre una partícula por campo de fuerza
\[\vecs F(x,y)=⟨y+\sin x,e^y−x⟩ \nonumber \]
ya que la partícula atraviesa el círculo\(x^2+y^2=4\) exactamente una vez en sentido contrario a las agujas del reloj, comenzando y terminando en el punto\((2,0)\).
Solución
Dejar\(C\) denotar el círculo y dejar\(D\) ser el disco encerrado por\(C\). El trabajo realizado sobre la partícula es
\[W=\oint_C (y+\sin x)\,dx+(e^y−x)\,dy. \nonumber \]
Al igual que con Ejemplo\(\PageIndex{1}\), esta integral se puede calcular utilizando herramientas que hemos aprendido, pero es más fácil usar la doble integral dada por el teorema de Green (Figura\(\PageIndex{5}\)).
Vamos\(\vecs F(x,y)=⟨P(x,y),Q(x,y)⟩=⟨y+\sin x,e^y−x⟩\). Entonces,\(Q_x=−1\) y\(P_y=1\). Por lo tanto,\(Q_x−P_y=−2\).
Por el teorema de Green,
\[\begin{align*} W &=\oint_C(y+\sin(x))dx+(e^y−x)\,dy \\[4pt] &=\iint_D (Q_x−P_y)\,dA \\[4pt] &=\iint_D−2\,dA \\[4pt] &=−2(area(D))=−2\pi (2^2)=−8\pi. \end{align*}\]
Usa el teorema de Green para calcular la integral de línea
\[\oint_C \sin(x^2)\,dx+(3x−y)\,dy. \nonumber \]
donde\(C\) es un triángulo rectángulo con vértices\((−1,2)\)\((4,2)\), y\((4,5)\) orientado en sentido antihorario.
- Pista
-
Transforma la línea integral en una doble integral.
- Contestar
-
\(\dfrac{45}{2}\)
En los dos ejemplos anteriores, la doble integral en el teorema de Green fue más fácil de calcular que la integral de línea, por lo que se utilizó el teorema para calcular la integral de línea. En el siguiente ejemplo, la doble integral es más difícil de calcular que la integral de línea, por lo que utilizamos el teorema de Green para traducir una doble integral en una integral de línea.
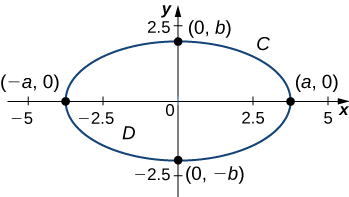
Calcular el área encerrada por elipse\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\) (Figura\(\PageIndex{6}\)).
Solución
Dejar\(C\) denotar la elipse y dejar que\(D\) sea la región encerrada por\(C\). Recordemos que la elipse se\(C\) puede parametrizar mediante
- \(x=a\cos t\),
- \(y=b \sin t\),
- \(0≤t≤2\pi\).
Calcular el área de\(D\) equivale a computar doble integral\(\iint_D \,dA\). Para calcular esta integral sin el teorema de Green, necesitaríamos\(D\) dividirnos en dos regiones: la región por encima del eje x y la región de abajo. El área de la elipse es
\[\int_{−a}^a\int_0^{\sqrt{b^2−{(bx/a)}^2}} \,dy\,dx+\int_{−a}^{a} \int_{−\sqrt{b^2−{(bx/a)}^2}}^{0} \,dy\,dx. \nonumber \]
Estas dos integrales no son sencillas de calcular (aunque cuando conocemos el valor de la primera integral, conocemos el valor de la segunda por simetría). En lugar de intentar calcularlos, usamos el teorema de Green para\(\iint_D \,dA\) transformarnos en una línea integral alrededor del límite\(C\).
Considerar el campo vectorial
\[F(x,y)=⟨P,Q⟩=⟨−\dfrac{y}{2},\dfrac{x}{2}⟩. \nonumber \]
Entonces,\(Q_x=\dfrac{1}{2}\) y\(P_y=−\dfrac{1}{2}\), y por lo tanto\(Q_x−P_y=1\). Aviso que\(\vecs F\) se eligió para tener la propiedad que\(Q_x−P_y=1\). Como este es el caso, el teorema de Green transforma la línea integral de\(\vecs F\) más\(C\) en la doble integral de 1 sobre\(D\).
Por el teorema de Green,
\[\begin{align*} \iint_D \,dA &=\iint_D (Q_x−P_y)\,dA \\[4pt] &=\int_C \vecs F\cdot d\vecs r=\dfrac{1}{2}\int_C −y\,dx+x\,dy \\[4pt] &=\dfrac{1}{2}\int_0^{2\pi}−b \sin t(−a\sin t)+a(\cos t)b\cos t\,dt \\[4pt] &=\dfrac{1}{2}\int_0^{2\pi} ab \cos^2 t+ab \sin^2 t\,dt \\[4pt] &=\dfrac{1}{2}\int_0^{2\pi} ab\,dt =\pi ab. \end{align*}\]
Por lo tanto, el área de la elipse es\(\pi ab\;\text{units}^2\).
En Ejemplo\(\PageIndex{3}\), utilizamos campo vectorial\(\vecs F(x,y)=⟨P,Q⟩=⟨−\dfrac{y}{2},\dfrac{x}{2}⟩\) para encontrar el área de cualquier elipse. La lógica del ejemplo anterior se puede extender para derivar una fórmula para el área de cualquier región\(D\). Let\(D\) ser cualquier región con un límite que sea una simple curva cerrada\(C\) orientada en sentido antihorario. Si\(F(x,y)=⟨P,Q⟩=⟨−\dfrac{y}{2},\dfrac{x}{2}⟩\), entonces\(Q_x−P_y=1\). Por lo tanto, por la misma lógica que en el Ejemplo\(\PageIndex{3}\),
\[ \text{area of} \; D=\iint_D dA=\dfrac{1}{2}\oint_C−ydx+xdy. \label{greenarea} \]
Vale la pena señalar que si\(F=⟨P,Q⟩\) hay algún campo vectorial con\(Q_x−P_y=1\), entonces la lógica del párrafo anterior funciona. Entonces. La ecuación\ ref {greenarea} no es la única ecuación que utiliza parciales mixtos de un campo vectorial para obtener el área de una región.
Encontrar el área de la región encerrada por la curva con parametrización\(r(t)=⟨\sin t\cos t,\sin t⟩\),\(0≤t≤\pi\).
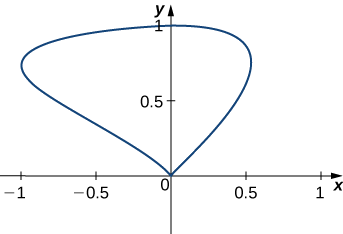
- Pista
-
Utilice la ecuación\ ref {greenarea}.
- Contestar
-
\(\dfrac{4}{3}\)
Forma de flujo del teorema de Green
La forma de circulación del teorema de Green relaciona una integral doble sobre región\(D\) a línea integral\(\oint_C \vecs F·\vecs Tds\), donde\(C\) está el límite de\(D\). La forma de flujo del teorema de Green relaciona una doble integral sobre la región\(D\) con el flujo a través del límite\(C\). El flujo de un fluido a través de una curva puede ser difícil de calcular usando la integral de la línea de flujo. Esta forma del teorema de Green nos permite traducir una integral de flujo difícil en una doble integral que a menudo es más fácil de calcular.
Let\(D\) Ser una región abierta, simplemente conectada con una curva límite\(C\) que es una curva cerrada simple, lisa por tramos que se orienta en sentido antihorario (Figura\(\PageIndex{7}\)). Let\(\vecs F=⟨P,Q⟩\) Ser un campo vectorial con funciones componentes que tienen derivadas parciales continuas en una región abierta que contiene\(D\). Entonces,
\[\oint_C \vecs F·\vecs N\,ds=\iint_D P_x+Q_y\,dA. \label{GreenN} \]
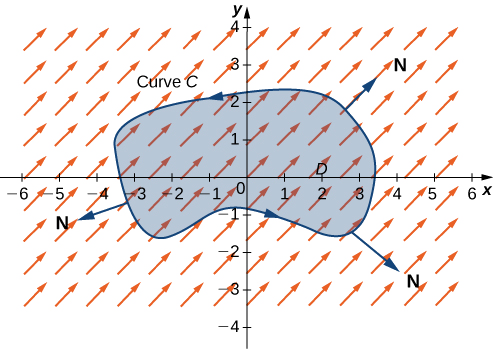
Debido a que esta forma del teorema de Green contiene vector normal unitario\(\vecs N\), a veces se le conoce como la forma normal del teorema de Green.
Recordemos eso\(\displaystyle \oint_C \vecs F·\vecs N\,ds=\oint_C −Q\,dx+P\,dy\). Dejar\(M=−Q\) y\(N=P\). Por la forma de circulación del teorema de Green,
\[\begin{align*} \oint_C−Q\,dx+P\,dy &=\oint_C M\,dx+N\,dy\\[4pt] &=\iint_D N_x−M_y \,dA\\[4pt] &=\iint_D P_x−{(−Q)}_y \,dA\\[4pt] &=\iint_D P_x+Q_y \,dA. \end{align*}\]
\(\square\)
Dejar\(C\) ser un círculo de radio\(r\) centrado en el origen (Figura\(\PageIndex{8}\)) y dejar\(\vecs F(x,y)=⟨x,y⟩\). Calcular el flujo a través\(C\).
Solución
Dejar\(D\) ser el disco encerrado por\(C\). El flujo a través\(C\) es\(\displaystyle \oint_C \vecs F·\vecs N\,ds\). Podríamos evaluar esta integral usando herramientas que hemos aprendido, pero el teorema de Green hace que el cálculo sea mucho más sencillo. Vamos\(P(x,y)=x\) y\(Q(x,y)=y\) para eso\(\vecs F=⟨P,Q⟩\). Tenga en cuenta que\(P_x=1=Q_y\), y por lo tanto\(P_x+Q_y=2\). Por el teorema de Green,
\[\int_C \vecs F\cdot\vecs N\,ds=\iint_D 2\,dA=2\iint_D \,dA. \nonumber \]
Ya que\(\displaystyle \iint_D \,dA\) es el área del círculo,\(\displaystyle \iint_D \,dA=\pi r^2\). Por lo tanto, el flujo a través\(C\) es\(2\pi r^2\).
Dejar\(S\) ser el triángulo con vértices\((0,0)\),\((1,0)\), y\((0,3)\) orientado en sentido horario (Figura\(\PageIndex{9}\)). Calcular el flujo de\(\vecs F(x,y)=⟨P(x,y),Q(x,y)⟩=⟨x^2+e^y,x+y⟩\) través\(S\).
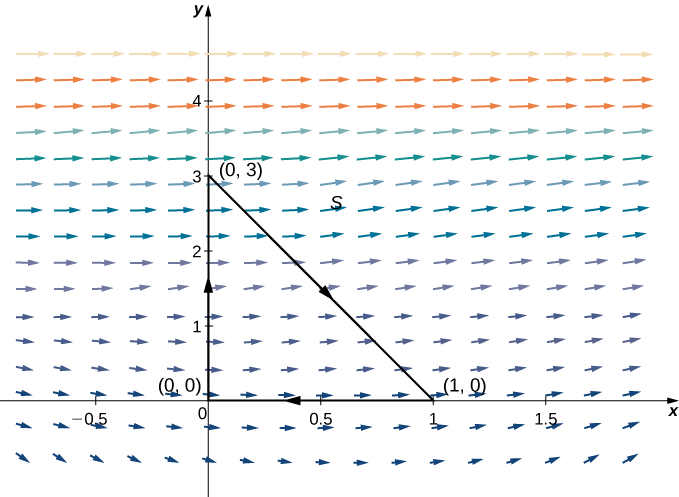
Solución
Para calcular el flujo sin el teorema de Green, necesitaríamos romper la integral de flujo en tres integrales de línea, una integral para cada lado del triángulo. Usar el teorema de Green para traducir la integral de línea de flujo en una sola integral doble es mucho más simple.
\(D\)Sea la región encerrada por\(S\). Tenga en cuenta que\(P_x=2x\) y\(Q_y=1\); por lo tanto,\(P_x+Q_y=2x+1\). El teorema de Green se aplica solo a las curvas cerradas simples orientadas en sentido antihorario, pero aún podemos aplicar el teorema porque\(\displaystyle \oint_C \vecs F·\vecs N\,ds=−\oint_{−S} \vecs F·\vecs N\,ds\) y\(−S\) está orientado en sentido antihorario. Según el teorema de Green, el flujo es
\[\begin{align*} \oint_C \vecs F·\vecs N\,ds &= \oint_{−S} \vecs F·\vecs N\,ds\\[4pt] &=−\iint_D (P_x+Q_y)\,dA \\[4pt] &=−\iint_D (2x+1)\,dA.\end{align*}\]
Observe que el borde superior del triángulo es la línea\(y=−3x+3\). Por lo tanto, en la doble integral iterada, los\(y\) -valores van de\(y=0\) a\(y=−3x+3\), y tenemos
\[\begin{align*} −\iint_D (2x+1)\,dA &= −\int_0^1\int_0^{−3x+3}(2x+1)\,dy\,dx \\[4pt] &=−\int_0^1(2x+1)(−3x+3)\,dx \\[4pt] &=−\int_0^1(−6x^2+3x+3)\,dx\\[4pt] &=−{[−2x^3+\dfrac{3x^2}{2}+3x]}_0^1 \\[4pt] &=−\dfrac{5}{2}. \end{align*}\]
Calcular el flujo de\(\vecs F(x,y)=⟨x^3,y^3⟩\) a través de un círculo unitario orientado en sentido antihorario.
- Pista
-
Aplica el teorema de Green y usa coordenadas polares.
- Contestar
-
\(\dfrac{3\pi}{2}\)
El agua fluye de un manantial ubicado en el origen. La velocidad del agua es modelada por el campo vectorial\(\vecs v(x,y)=⟨5x+y,x+3y⟩\) m/seg. Encuentra la cantidad de agua por segundo que fluye a través del rectángulo con vértices\((−1,−2)\),,\((1,−2)\)\((1,3)\), y\((−1,3)\), orientados en sentido antihorario (Figura\(\PageIndex{10}\)).
Solución
Dejar\(C\) representar el rectángulo dado y dejar\(D\) ser la región rectangular encerrada por\(C\). Para encontrar la cantidad de agua que fluye a través\(C\), calculamos el flujo\(\int_C \vecs v\cdot d\vecs r\). Vamos\(P(x,y)=5x+y\) y\(Q(x,y)=x+3y\) para eso\(\vecs v=⟨P,Q⟩\). Entonces,\(P_x=5\) y\(Q_y=3\). Por el teorema de Green,
\[\begin{align*} \int_C \vecs v\cdot d\vecs r &=\iint_D (P_x+Q_y)\,dA \\ &=\iint_D 8\,dA \\ &=8(area\space of\space D)=80. \end{align*}\]
Por lo tanto, el flujo de agua es de 80 m 2 /seg.
Recordemos que si el campo vectorial\(\vecs F\) es conservador, entonces\(\vecs F\) no funciona alrededor de curvas cerradas, es decir, la circulación de\(\vecs F\) alrededor de una curva cerrada es cero. De hecho, si el dominio de\(\vecs F\) está simplemente conectado, entonces\(\vecs F\) es conservador si y sólo si la circulación de\(\vecs F\) alrededor de cualquier curva cerrada es cero. Si reemplazamos “circulación de\(\vecs F\)” por “flujo de”\(\vecs F\), entonces obtenemos una definición de un campo vectorial libre de fuente. Las siguientes declaraciones son todas formas equivalentes de definir un campo libre de origen\(\vecs F=⟨P,Q⟩\) en un dominio simplemente conectado (tenga en cuenta las similitudes con las propiedades de los campos vectoriales conservadores):
- El flujo\( \displaystyle \oint_C \vecs F·\vecs N\,ds\) a través de cualquier curva cerrada\(C\) es cero.
- Si\(C_1\) y\(C_2\) son curvas en el dominio de\(\vecs F\) con los mismos puntos de partida y puntos finales, entonces\(\displaystyle \int_{C_1} \vecs F·\vecs N\,ds=\int_{C_2} \vecs F·\vecs N\,ds\). En otras palabras, el flujo es independiente del camino.
- Hay una función de flujo\(g(x,y)\) para\(\vecs F\). Una función de corriente para\(\vecs F=⟨P,Q⟩\) es una función g tal que\(P=g_y\) y\(Q=−g_x\) .Geométricamente,\(\vecs F=\langle a,b\rangle\) es tangencial a la curva de nivel de\(g\) at\((a,b)\). Dado que el gradiente de\(g\) es perpendicular a la curva de nivel de\(g\) at\((a,b)\), la función stream\(g\) tiene la propiedad\(\vecs F(a,b)\cdot\vecs\nabla g(a,b)=0\) para cualquier punto\((a,b)\) en el dominio de\(g\). (Las funciones Stream desempeñan el mismo papel para los campos libres de origen que las funciones potenciales juegan para los campos conservadores).
- \(P_x+Q_y=0\)
Verifique que el campo vectorial de rotación\(\vecs F(x,y)=⟨y,−x⟩\) esté libre de origen y encuentre una función de flujo para\(\vecs F\).
Solución
Tenga en cuenta que el dominio de\(\vecs F\) es todo\(ℝ^2\), que simplemente está conectado. Por lo tanto, para mostrar que\(\vecs F\) es fuente libre, podemos mostrar cualquiera de los ítems 1 a 4 de la lista anterior para que sea cierto. En este ejemplo, mostramos que el ítem 4 es verdadero. Dejar\(P(x,y)=y\) y\(Q(x,y)=−x\). Entonces\(P_x+0=Q_y\), y por lo tanto\(P_x+Q_y=0\). Así,\(\vecs F\) es fuente libre.
Para encontrar una función de flujo para\(\vecs F\), proceda de la misma manera que encontrar una función potencial para un campo conservador. Dejar\(g\) ser una función de flujo para\(\vecs F\). Entonces\(g_y=y\), lo que implica que
\(g(x,y)=\dfrac{y^2}{2}+h(x)\).
Ya que\(−g_x=Q=−x\), tenemos\(h′(x)=x\). Por lo tanto,
\(h(x)=\dfrac{x^2}{2}+C\).
Dejar\(C=0\) da la función de flujo
\(g(x,y)=\dfrac{x^2}{2}+\dfrac{y^2}{2}\).
Para confirmar que\(g\) es una función de flujo para\(\vecs F\), tenga en cuenta que\(g_y=y=P\) y\(−g_x=−x=Q\).
Observe que el campo vectorial de rotación libre de fuente\(\vecs F(x,y)=⟨y,−x⟩\) es perpendicular al campo vectorial radial conservador\(\vecs \nabla g=⟨x,y⟩\) (Figura\(\PageIndex{11}\)).
Encuentra una función de flujo para el campo vectorial\(\vecs F(x,y)=⟨x \sin y,\cos y⟩\).
- Pista
-
Siga el esquema proporcionado en el ejemplo anterior.
- Contestar
-
\(g(x,y)=−x\cos y\)
Los campos vectoriales que son conservadores y libres de origen son campos vectoriales importantes. Una característica importante de los campos vectoriales conservadores y libres de fuentes en un dominio simplemente conectado es que cualquier función potencial\(f\) de dicho campo satisface la ecuación de Laplace\(f_{xx}+f_{yy}=0\). La ecuación de Laplace es fundamental en el campo de las ecuaciones diferenciales parciales porque modela fenómenos como los potenciales gravitacionales y magnéticos en el espacio, y el potencial de velocidad de un fluido ideal. Una función que satisface la ecuación de Laplace se denomina función armónica. Por lo tanto, cualquier función potencial de un campo vectorial conservador y libre de fuentes es armónica.
Para ver que cualquier función potencial de un campo vectorial conservador y libre de fuente en un dominio simplemente conectado es armónica, deja\(f\) ser tal función potencial de campo vectorial\(\vecs F=⟨P,Q⟩\). Entonces,\(f_x=P\) y\(f_x=Q\) porque\(\vecs \nabla f=\vecs F\). Por lo tanto,\(f_{xx}=P_x\) y\(f_{yy}=Q_y\). Ya que\(\vecs F\) es fuente libre\(f_{xx}+f_{yy}=P_x+Q_y=0\),, y tenemos que\(f\) es armónico.
Para el campo vectorial\(\vecs F(x,y)=⟨e^x\sin y,e^x\cos y⟩\), verifique que el campo sea conservador y libre de fuentes, encuentre una función potencial para\(\vecs F\), y verifique que la función potencial sea armónica.
Solución
Dejar\(P(x,y)=e^x\sin y\) y\(Q(x,y)=e^x \cos y\). Observe que el dominio de\(\vecs F\) es todo de dos espacios, que simplemente está conectado. Por lo tanto, podemos verificar los interparciales de\(\vecs F\) para determinar si\(\vecs F\) es conservador. Tenga en cuenta que\(P_y=e^x \cos y=Q_x\), también lo\(\vecs F\) es conservador. Desde\(P_x=e^x \sin y\) y\(Q_y=e^x \sin y\),\(P_x+Q_y=0\) y el campo es fuente libre.
Para encontrar una función potencial para\(\vecs F\), dejar\(f\) ser una función potencial. Entonces,\(\vecs \nabla f=\vecs F\), entonces\(f_x(x,y)=e^x \sin y\). Integrando esta ecuación con respecto a x da\(f(x,y)=e^x \sin y+h(y)\). Ya que\(f_y(x,y)=e^x \cos y\), diferenciando\(f\) con respecto a y da\(e^x\cos y=e^x\cos y+h′(y)\). Por lo tanto, podemos tomar\(h(y)=0\), y\(f(x,y)=e^x\sin y\) es una función potencial para\(f\).
Para verificar que\(f\) es una función armónica, tenga en cuenta que\(f_{xx}(x,y)=\dfrac{\partial}{\partial x}(e^x\sin y)=e^x \sin y\) y
\(f_{yy}(x,y)=\dfrac{\partial}{\partial x}(e^x\cos y)=−e^x\sin y\). Por lo tanto\(f_{xx}+f_{yy}=0\),, y\(f\) satisface la ecuación de Laplace.
¿La función es\(f(x,y)=e^{x+5y}\) armónica?
- Pista
-
Determinar si la función satisface la ecuación de Laplace.
- Contestar
-
No
Teorema de Green sobre las Regiones Generales
El teorema de Green, como se ha dicho, se aplica solo a regiones que simplemente están conectadas, es decir, el teorema de Green como se ha dicho hasta ahora no puede manejar regiones con agujeros. Aquí, extendemos el teorema de Green para que funcione en regiones con muchos agujeros finitamente (Figura\(\PageIndex{12}\)).
Antes de discutir las extensiones del teorema de Green, necesitamos repasar alguna terminología con respecto al límite de una región. Dejar\(D\) ser una región y dejar\(C\) ser un componente del límite de\(D\). Decimos que\(C\) está orientado positivamente si, a medida que caminamos\(C\) en dirección de orientación, la región siempre\(D\) está a nuestra izquierda. Por lo tanto, la orientación en sentido antihorario del límite de un disco es una orientación positiva, por ejemplo. \(C\)La curva se orienta negativamente si, a medida que caminamos\(C\) en dirección de orientación, la región siempre\(D\) está a nuestra derecha. La orientación en el sentido de las agujas del reloj del límite de un disco es una orientación negativa, por ejemplo.
Dejar\(D\) ser una región con finitamente muchos agujeros (de modo que\(D\) tiene finitamente muchas curvas de límite), y denotar el límite de\(D\) por\(\partial D\) (Figura\(\PageIndex{13}\)). Para extender el teorema de Green para que pueda manejarlo\(D\), dividimos región\(D\) en dos regiones,\(D_1\)\(\partial D_1\) y\(D_2\) (con límites respectivos y\(\partial D_2\)), de tal manera que\(D=D_1\cup D_2\) y\(D_1\) ni\(D_2\) tiene agujeros (Figura\(\PageIndex{13}\)).
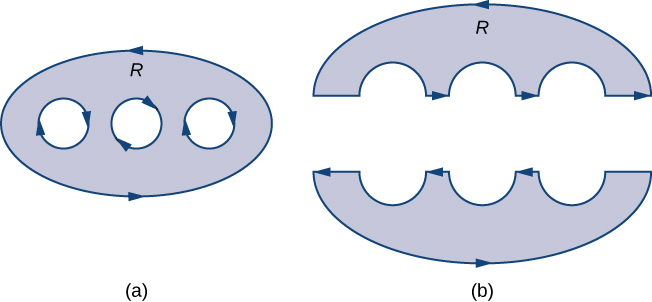
Supongamos que el límite de\(D\) está orientado como en la figura, con los agujeros internos dados una orientación negativa y el límite exterior dado una orientación positiva. El límite de cada región simplemente conectada\(D_1\) y\(D_2\) está orientada positivamente. Si\(\vecs F\) es un campo vectorial definido en\(D\), entonces el teorema de Green dice que
\[\begin{align} \oint_{\partial D} \vecs F·d\vecs{r} &=\oint_{\partial D_1}\vecs F·d\vecs{r}+\oint_{\partial D_2}\vecs F·d\vecs{r} \\ &=\iint_{D_1}Q_x−P_y\,dA+\iint_{D_2}Q_x−P_y\,dA \\ &=\iint_D (Q_x−P_y)\,dA.\end{align} \nonumber \]
Por lo tanto, el teorema de Green aún funciona en una región con agujeros.
Para ver cómo funciona esto en la práctica, considere el anillo\(D\) en la Figura\(\PageIndex{14}\) y supongamos que\(F=⟨P,Q⟩\) es un campo vectorial definido sobre este anillo. Región\(D\) tiene un agujero, por lo que no está simplemente conectada. Orientar el círculo exterior del anillo en sentido antihorario y el círculo interno en sentido horario (Figura\(\PageIndex{14}\)) para que, cuando dividamos la región en\(D_1\) y\(D_2\), seamos capaces de mantener la región a nuestra izquierda mientras caminamos por un sendero que atraviesa el límite. Dejar\(D_1\) ser la mitad superior del anillo y\(D_2\) ser la mitad inferior. Ninguna de estas regiones tiene agujeros, por lo que hemos\(D\) dividido en dos regiones simplemente conectadas.
Etiquetamos cada pieza de estos nuevos límites como\(P_i\) para algunos\(i\), como en la Figura\(\PageIndex{14}\). Si comenzamos en\(P\) y viajamos a lo largo del límite orientado, el primer segmento es\(P_1\), entonces\(P_2\),\(P_3\), y\(P_4\). Ahora hemos atravesado\(D_1\) y vuelto a\(P\). A continuación, empezamos de\(P\) nuevo y atravesamos\(D_2\). Dado que la primera pieza del límite es la misma que\(P_4\) en\(D_1\), pero orientada en sentido contrario, la primera pieza de\(D_2\) es\(−P_4\). A continuación, tenemos\(P_5\), entonces\(−P_2\), y finalmente\(P_6\).
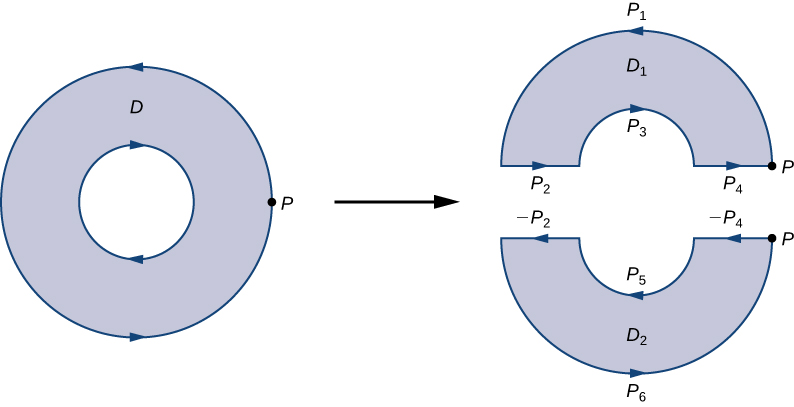
La figura\(\PageIndex{14}\) muestra un camino que atraviesa el límite de\(D\). Observe que esta ruta atraviesa el límite de la región\(D_1\), vuelve al punto de partida y, a continuación, atraviesa el límite de la región\(D_2\). Además, a medida que caminamos por el sendero, la región está siempre a nuestra izquierda. Observe que este recorrido de los\(P_i\) caminos cubre todo el límite de la región\(D\). Si solo hubiéramos atravesado una porción del límite de\(D\), entonces no podemos aplicar el teorema de Green a\(D\).
El límite de la mitad superior del anillo, por lo tanto, es\(P_1\cup P_2\cup P_3\cup P_4\) y el límite de la mitad inferior del anillo es\(−P_4\cup P_5\cup −P_2\cup P_6\). Entonces, el teorema de Green implica
\[\begin{align} \oint_{\partial D}\vecs F·d\vecs{r} &=\int_{P_1}\vecs F·d\vecs{r}+\int_{P_2}\vecs F·d\vecs{r}+\int_{P_3}\vecs F·d\vecs{r}+\int_{P_4}\vecs F·d\vecs{r}+\int_{−P_4}\vecs F·d\vecs{r}+\int_{P_5}\vecs F·d\vecs{r}+\int_{−P_2}\vecs F·d\vecs{r}+\int_{P_6}\vecs F·d\vecs{r} \\ &=\int_{P_1}\vecs F·d\vecs{r}+\int_{P_2}\vecs F·d\vecs{r}+\int_{P_3}\vecs F·d\vecs{r}+\int_{P_4}\vecs F·d\vecs{r}+\int_{P_4}\vecs F·d\vecs{r}+\int_{P_5}\vecs F·d\vecs{r}+\int_{−P_2}\vecs F·d\vecs{r}+\int_{P_6}\vecs F·d\vecs{r} \\ &=\int_{P_1}\vecs F·d\vecs{r}+\int_{P_3}\vecs F·d\vecs{r}+\int_{P_5}\vecs F·d\vecs{r}+\int_{P_6}\vecs F·d\vecs{r} \\ &=\oint_{\partial D_1}\vecs F·d\vecs{r}+\oint_{\partial D_2}\vecs F·d\vecs{r}\\ &=\iint_{D_1}(Q_x−P_y)\,dA+\iint_{D_2}(Q_x−P_y)\,dA \\ &=\iint_D(Q_x−P_y)\,dA. \end{align} \nonumber \]
Por lo tanto, llegamos a la ecuación que se encuentra en el teorema de Green, es decir,
\[\oint_{\partial D}\vecs F·d\vecs{r}=\iint_D (Q_x−P_y)\,dA. \nonumber \]
La misma lógica implica que la forma de flujo del teorema de Green también se puede extender a una región con muchos agujeros finitamente:
\[\oint_C F·N\,ds=\iint_D (P_x+Q_y)\,dA. \nonumber \]
Calcular la integral
\[\oint_{\partial D}(\sin x−\dfrac{y^3}{3})dx+(\dfrac{y^3}{3}+\sin y)dy, \nonumber \]
donde\(D\) está el anillo dado por las desigualdades polares\(1≤r≤2\),\(0≤\theta≤2\pi\).
Solución
Aunque no\(D\) está simplemente conectado, podemos usar la forma extendida del teorema de Green para calcular la integral. Dado que la integración ocurre sobre un anillo, convertimos a coordenadas polares:
\[\begin{align*} \oint_{\partial D}(\sin x−\dfrac{y^3}{3})\,dx+(\dfrac{x^3}{3}+\sin y)\,dy &=\iint_D (Q_x−P_y)\,dA \\ &=\iint_D (x^2+y^2)\,dA\\ &=\int_0^{2\pi}\int_1^2 r^3\,drd\theta=\int_0^{2\pi} \dfrac{15}{4}\,d\theta \\ &=\dfrac{15\pi}{2}. \end{align*}\]
Dejar\(\vecs F=⟨P,Q⟩=⟨\dfrac{y}{x^2+y^2},-\dfrac{x}{x^2+y^2}⟩\) y dejar\(C\) ser cualquier simple curva cerrada en un plano orientado en sentido antihorario. ¿Cuáles son los valores posibles de\(\oint_C \vecs F·d\vecs{r}\)?
Solución
Usamos la forma extendida del teorema de Green para mostrar que\(\oint_C \vecs F·d\vecs{r}\) es\(0\) o\(−2\pi\) —es decir, no importa cuán loca\(C\) sea la curva, la línea integral de\(\vecs F\) lo largo\(C\) puede tener solo uno de los dos valores posibles. Consideramos dos casos: el caso cuando\(C\) abarca el origen y el caso cuando\(C\) no abarca el origen.
Caso 1: C no abarca el origen
En este caso, la región encerrada simplemente\(C\) se conecta porque el único agujero en el dominio de\(\vecs F\) está en el origen. Mostramos en nuestra discusión de los partidos cruzados que\(\vecs F\) satisfacen la condición de parcialidad cruzada. Si restringimos el dominio de\(\vecs F\) solo a\(C\) y la región que encierra, entonces\(\vecs F\) con este dominio restringido ahora se define en un dominio simplemente conectado. Dado que\(\vecs F\) satisface la propiedad transversal parcial en su dominio restringido, el campo\(\vecs F\) es conservador en esta región simplemente conectada y por lo tanto la circulación\(\oint_C \vecs F·d\vecs{r}\) es cero.
Caso 2: C Abarca el Origen
En este caso, la región encerrada no\(C\) está simplemente conectada porque esta región contiene un agujero en el origen. Dejar\(C_1\) ser un círculo de radio a centrado en el origen de manera que\(C_1\) quede completamente dentro de la región encerrada por\(C\) (Figura\(\PageIndex{15}\)). Dar\(C_1\) una orientación en sentido horario.
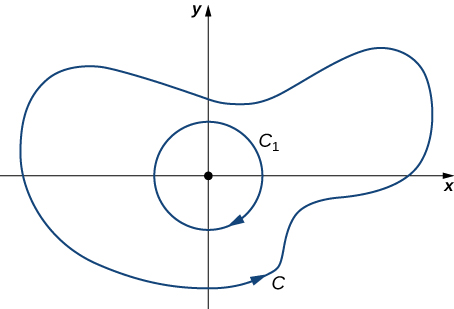
Dejar\(D\) ser la región entre\(C_1\) y\(C\), y\(C\) se orienta en sentido antihorario. Por la versión extendida del teorema de Green,
\[\begin{align*} \int_C \vecs F·d\vecs{r}+\int_{C_1}\vecs F·d\vecs{r} &=\iint_D Qx_−P_y \,dA \\[4pt] &=\iint_D−\dfrac{y^2−x^2}{{(x^2+y^2)}^2}+\dfrac{y^2−x^2}{{(x^2+y^2)}^2}dA \\[4pt] &=0, \end{align*}\]
y por lo tanto
\[\int_C \vecs F·d\vecs{r}=−\int_{C_1} \vecs F·d\vecs{r}. \nonumber \]
Ya que\(C_1\) es una curva específica, podemos evaluar\(\int_{C_1}\vecs F·d\vecs{r}\). Vamos
\[ x=a\cos t, \;\; y=a\sin t, \;\; 0≤t≤2\pi \nonumber \]
ser una parametrización de\(C_1\). Entonces,
\[\begin{align*} \int_{C_1}\vecs F·d\vecs{r} &=\int_0^{2\pi} F(r(t))·r′(t)dt \\[4pt] &=\int_0^{2\pi} ⟨−\dfrac{\sin(t)}{a},−\dfrac{\cos(t)}{a}⟩·⟨−a\sin(t),−a\cos(t)⟩dt \\[4pt] &=\int_0^{2\pi}{\sin}^2(t)+{\cos}^2(t)dt \\[4pt] &=\int_0^{2\pi}dt=2\pi. \end{align*}\]
Por lo tanto,\(\int_C F·ds=−2\pi\).
Calcular integral\(\oint_{\partial D}\vecs F·d\vecs{r}\), donde\(D\) está el anillo dado por las desigualdades polares\(2≤r≤5\),\(0≤\theta≤2\pi\), y\(F(x,y)=⟨x^3,5x+e^y\sin y⟩\).
- Pista
-
Utilice la versión extendida del teorema de Green.
- Contestar
-
\(105\pi\)
Imagina que eres un médico que acaba de recibir una imagen de resonancia magnética del cerebro de tu paciente. El cerebro tiene un tumor (Figura\(\PageIndex{16}\)). ¿Qué tan grande es el tumor? Para ser precisos, ¿cuál es la zona de la región roja? La sección transversal roja del tumor tiene una forma irregular, por lo que es poco probable que se pueda encontrar un conjunto de ecuaciones o desigualdades para la región y luego poder calcular su área por medios convencionales. Se podría aproximar el área cortando la región en minúsculos cuadrados (un enfoque de suma de Riemann), pero este método siempre da una respuesta con algún error.
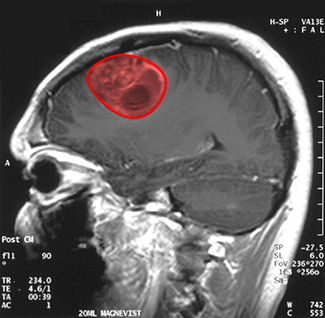
En lugar de intentar medir el área de la región directamente, podemos usar un dispositivo llamado planímetro rodante para calcular exactamente el área de la región, simplemente midiendo su límite. En este proyecto investigas cómo funciona un planímetro, y usas el teorema de Green para mostrar que el dispositivo calcula el área correctamente.
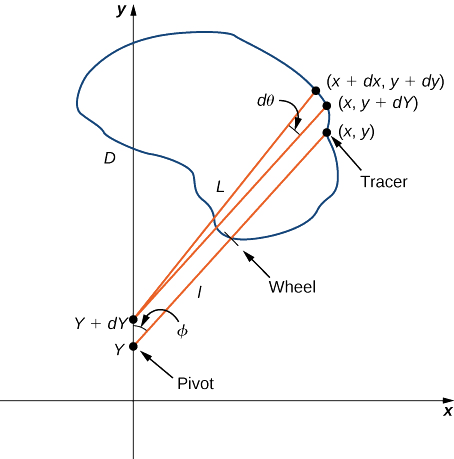
Un planímetro rodante es un dispositivo que mide el área de una región plana trazando el límite de esa región (Figura\(\PageIndex{17}\)). Para medir el área de una región, simplemente corremos el trazador del planímetro alrededor del límite de la región. El planímetro mide el número de vueltas a través de las cuales gira la rueda a medida que trazamos el límite; el área de la forma es proporcional a este número de vueltas de rueda. Podemos derivar la ecuación de proporcionalidad precisa usando el teorema de Green. A medida que el trazador se mueve alrededor del límite de la región, el brazo trazador gira y el rodillo se mueve hacia adelante y hacia atrás (pero no gira).
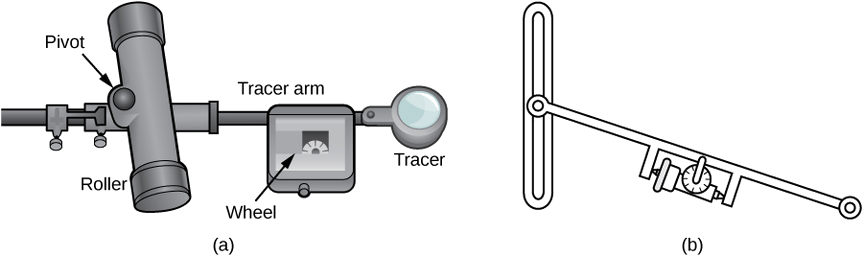
Dejar\(C\) denotar el límite de región\(D\), el área a calcular. A medida que el trazador atraviesa la curva\(C\), supongamos que el rodillo se mueve a lo largo del eje y (ya que el rodillo no gira, se puede suponer que se mueve a lo largo de una línea recta). Utilice las coordenadas\((x,y)\) para representar puntos en el límite\(C\) y las coordenadas\((0,Y)\) para representar la posición del pivote. A medida que el planímetro traza\(C\), el pivote se mueve a lo largo del eje y mientras que el brazo trazador gira sobre el pivote.
Mira una breve animación de un planímetro en acción.
Comience el análisis considerando el movimiento del trazador a medida que se mueve desde un punto en\((x,y)\) sentido antihorario hasta un punto\((x+dx,y+dy)\) cercano a\((x,y)\) (Figura\(\PageIndex{18}\)). El pivote también se mueve, de punto\((0,Y)\) a punto cercano\((0,Y+dY)\). ¿Cuánto gira la rueda como resultado de este movimiento? Para responder a esta pregunta, rompa el movimiento en dos partes. Primero, haga rodar el pivote a lo largo del eje y de\((0,Y)\) a\((0,Y+dY)\) sin girar el brazo trazador. El brazo trazador termina entonces en un punto\((x,y+dY)\) manteniendo un ángulo constante\(\phi\) con el eje x. Segundo, gire el brazo trazador un ángulo\(d\theta\) sin mover el rodillo. Ahora el trazador está en el punto\((x+dx,y+dy)\). Deje que ll sea la distancia desde el pivote a la rueda y deje que L sea la distancia desde el pivote hasta el trazador (la longitud del brazo trazador).
- Explique por qué es la distancia total por la que rueda la rueda el pequeño movimiento que se acaba de describir es\(\sin \phi dY+ld\theta=\dfrac{x}{L}dY+ld\theta\)
- \(\oint_C d\theta=0\)Demuéstralo.
- Utilice el paso 2 para mostrar que la distancia total de rodadura de la rueda a medida que el trazador atraviesa la curva\(C\) es el balanceo
total de la rueda\(=\dfrac{1}{L}\oint_C xdY\).
Ahora que tienes una ecuación para la distancia total de rodadura de la rueda, conecta esta ecuación al teorema de Green para calcular el área\(D\) encerrada por\(C\). - \(x^2+(y−Y)^2=L^2\)Demuéstralo.
- Supongamos que la orientación del planímetro es como se muestra en la Figura\(\PageIndex{18}\). Explique por qué\(Y≤y\), y utilice esta desigualdad para mostrar que hay un valor único de\(Y\) para cada punto\((x,y)\):\(Y=y=\sqrt{L^2−x^2}\).
- Usa el paso 5 para demostrar que\(dY=dy+\dfrac{x}{L^2−x^2}dx.\)
- Usa el teorema de Green para demostrarlo\(\displaystyle \oint_C \dfrac{x}{L^2−x^2}dx=0\).
- Use el paso 7 para mostrar que el rollo total de la rueda es
\[\text{Total wheel roll}\quad =\quad 1L\oint_C x\,dy. \nonumber \]
Tomó un poco de trabajo, pero esta ecuación dice que la variable de integración Y en el paso 3 puede ser reemplazada por y.
- Usa el teorema de Green para mostrar que el área de\(D\) es\(\oint_C xdy\). La lógica es similar a la lógica utilizada para mostrar que el área de\(\displaystyle D=12\oint_C −y\,dx+x\,dy\).
- Concluir que el área de\(D\) es igual a la longitud del brazo trazador multiplicado por la distancia total de rodadura de la rueda.
Ya sabes cómo funciona un planímetro y has utilizado el teorema de Green para justificar que funciona. Para calcular el área de una región plana\(D\), utilice un planímetro para trazar el límite de la región. El área de la región es la longitud del brazo trazador multiplicada por la distancia que rodó la rueda.
Conceptos clave
- El teorema de Green relaciona la integral sobre una región conectada con una integral sobre el límite de la región. El teorema de Green es una versión del Teorema Fundamental del Cálculo en una dimensión superior.
- El teorema de Green viene en dos formas: una forma de circulación y una forma de flujo. En la forma de circulación, el integrando es\(\vecs F·\vecs T\). En la forma de flujo, el integrando es\(\vecs F·\vecs N\).
- El teorema de Green se puede utilizar para transformar una integral de línea difícil en una doble integral más fácil, o para transformar una integral doble difícil en una integral de línea más fácil.
- Un campo vectorial es fuente libre si tiene una función de flujo. El flujo de un campo vectorial libre de fuente a través de una curva cerrada es cero, así como la circulación de un campo vectorial conservador a través de una curva cerrada es cero.
Ecuaciones Clave
- Teorema de Green, forma de circulación
\(\displaystyle ∮_C P\,dx+Q\,dy=∬_D Q_x−P_y\,dA\), donde\(C\) está el límite de\(D\) - Teorema de Green, forma de flujo
\(\displaystyle ∮_C\vecs F·\vecs N\,ds=∬_D P_x+Q_y\,dA\), donde\(C\) está el límite de\(D\) - Teorema de Green, versión extendida
\(\displaystyle ∮_{\partial D}\vecs F·d\vecs{r}=∬_D Q_x−P_y\,dA\)
Glosario
- Teorema de Green
- relaciona la integral sobre una región conectada con una integral sobre el límite de la región
- función stream
- si\(\vecs F=⟨P,Q⟩\) es un campo vectorial libre de fuente, entonces la función de flujo\(g\) es una función tal que\(P=g_y\) y\(Q=−g_x\)