1.4: Productos cruzados

En la Sección 1.3 definimos el producto punto, lo que dio una forma de multiplicar dos vectores. El producto resultante, sin embargo, fue un escalar, no un vector. En esta sección definiremos un producto de dos vectores que sí resultan en otro vector. Este producto, llamado el producto cruzado, solo se define para vectores en\(\mathbb{R}^{3}\). La definición puede parecer extraña y carente de motivación, pero veremos en breve las bases geométricas para ello.

Definición 1.8

Dejar\(\textbf{v} = (v_{1}, v_{2}, v_{3})\) y\(\textbf{w} = (w_{1}, w_{2}, w_{3})\) ser vectores en\(\mathbb{R}^{3}\). El\(\textbf{cross product}\) de\(\textbf{v}\) y\(\textbf{w}\), denotado por\(\textbf{v} \times \textbf{w}\), es el vector en\(\mathbb{R}^{3}\) dado por:

\[\textbf{v} \times \textbf{w} = (v_{2}w_{3} - v_{3}w_{2}, v_{3}w_{1} - v_{1}w_{3}, v_{1}w_{2} - v_{2}w_{1})\]

Ejemplo 1.7

Encuentra\(\textbf{i} \times \textbf{j}\).

Solución

Desde\(\textbf{i} = (1,0,0)\) y\(\textbf{j} = (0,1,0)\), entonces
\ begin {align*}
\ textbf {i}\ times\ textbf {j} &= ((0) (0) - (0) (1), (0) (0) (0) - (1) (0), (1) (0) - (0) (0))\ [4pt]
&= (0,0,1)\ [4pt]
&=\ tbtexf {k}
\ final {alinear*}

De igual manera se puede demostrar que\(\textbf{j} \times \textbf{k} = \textbf{i}\) y\(\textbf{k} \times \textbf{i} = \textbf{j}\).

Figura 1.4.1

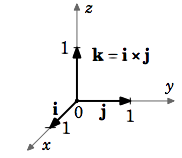
En el ejemplo anterior, el producto cruzado de los vectores dados fue perpendicular a ambos vectores. Resulta que este siempre será el caso.

Teorema 1.11

Si el producto cruzado\(\textbf{v} \times \textbf{w}\) de dos vectores distintos de cero\(\textbf{v}\) y también\(\textbf{w}\) es un vector distinto de cero, entonces es perpendicular a ambos\(\textbf{v}\) y\(\textbf{w}\).

Prueba

Mostraremos que\((\textbf{v} \times \textbf{w}) \cdot \textbf{v} = 0\):
\ begin {align*}
(\ textbf {v}\ times\ textbf {w})\ cdot\ textbf {v} &= (v_ {2} w_ {3} - v_ {3} w_ {2}, v_ {3} w_ {1} - v_ {1} w_ {3}, v_ {1} w_ {2} - v_ {2} w_ {1})\ cdot (v_ {1}, v_ {2}, v_ {3})\\ [4pt]
&= v_ {2} w_ {3} v_ {1} - v_ {3} w_ {2} v_ {1} +
v_ {3} w_ {1} v_ {2} - v_ {1} w_ {3} v_ {2} + v_ {1} w_ {2} v_ {3} -
v_ {2} w_ {1} v_ {3}\\ [4pt]
&= v_ {1} v_ {2} w_ {3} - v_ {1} v_ {2} w_ {3} + w_ {1} v_ {2} v_ {3} -
w_ {1} v_ {2} v_ {3} + v_ {1} w_ {2} v_ {3} - v_ {1} w_ {2} v_ {3}\\ [4pt]
&= 0\ text {, después de reorganizar los términos.}
\ end {align*}
\(\therefore \textbf{v} \times \textbf{w} \perp \textbf{v}\) por Corolario 1.7. La prueba que\(\textbf{v} \times \textbf{w} \perp \textbf{w}\) es similar.

\(\square\)

Como consecuencia del teorema y teorema 1.9 anteriores, tenemos lo siguiente:

Corolario 1.12

Si el producto cruzado\(\textbf{v} \times \textbf{w}\) de dos vectores distintos de cero\(\textbf{v}\) y también\(\textbf{w}\) es un vector distinto de cero, entonces es perpendicular al lapso de\(\textbf{v}\) y\(\textbf{w}\).

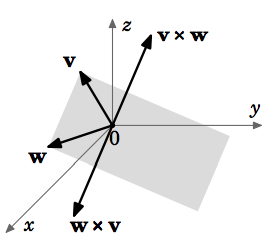
El lapso de dos vectores no paralelos distintos de cero\(\textbf{v}, \textbf{w}\) en\(\mathbb{R}^{3}\) es un plano\(P\), por lo que el corolario anterior muestra que\(\textbf{v} \times \textbf{w}\) es perpendicular a ese plano. Como se muestra en la Figura 1.4.2, existen dos direcciones posibles para\(\textbf{v} \times \textbf{w}\), una la opuesta a la otra. Resulta (ver Apéndice B) que la dirección de\(\textbf{v} \times \textbf{w}\) la viene dada por los\(\textit{right-hand rule}\), es decir, los vectores\(\textbf{v}, \textbf{w}\),\(\textbf{v} \times \textbf{w}\) forman un sistema diestro. Recuerda de la Sección 1.1 que esto significa que puedes apuntar el pulgar hacia arriba en la dirección de\(\textbf{v} \times \textbf{w}\) mientras giras\(\textbf{v}\) hacia\(\textbf{w}\) con los cuatro dedos restantes.

Figura 1.4.2 Dirección de v × w

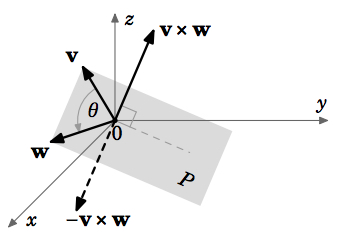
Ahora derivaremos una fórmula para la magnitud de\(\textbf{v} \times \textbf{w}\), para vectores distintos de cero\(\textbf{v}, \textbf{w}:\)

\ begin {alinear*}
\ norm {\ textbf {v}\ times\ textbf {w}} ^ {2} &= (v_ {2} w_ {3} - v_ {3} w_ {2}) ^ {2} +
(v_ {3} w_ {1} - v_ {1} w_ {3}) ^ {2} + (v_ {1} w_ {2} - v_ {2} w_ {1}) ^ {2}\\ [4pt]
&= v_ {2} ^ {2} w_ {3} ^ {2} - 2v_ {2} w_ {2} v_ {3} w_ {3} + v_ {3} ^ {2} w_ {2} ^ {2} +
v_ {3} ^ {2} w_ {1} ^ {2} - 2v_ {1} w_ {1} v_ {3} w_ {3} + v_ {1} ^ {2} w_ {3} ^ {2} +
v_ {1} ^ {2} w_ {2} ^ {2} - 2v_ {1} w_ {1} v_ {2} w_ {2} + v_ {2} ^ {2} w_ {1} ^ {2}\\ [4pt]
&= v_ {1} ^ {2} (w_ {2} ^ {2} + w_ {3} ^ {2}) + v_ {2} ^ {2} (w_ {1} ^ {2} + w_ {3} ^ {2}) +
v_ {3} ^ {2} (w_ {1} ^ {2} + w_ {2} ^ {2})
- 2 (v_ {1} w_ {1} v_ {2} w_ {2} +
v_ {1} w_ {1} v_ {3} w_ {3} + v_ {2} w_ {2} v_ {3} w_ {3})\ final {alinear*}

y ahora sumando y restando\(v_{1}^{2}w_{1}^{2}\),\(v_{2}^{2}w_{2}^{2}\), y\(v_{3}^{2}w_{3}^{2}\) en el lado derecho da

\ begin {alinear*} & = v_ {1} ^ {2} (w_ {1} ^ {2} + w_ {2} ^ {2} + w_ {3} ^ {2}) + v_ {2} ^ {2} (w_ {1} ^ {2} + w_ {2} ^ {2} + w_ {3} ^ {2}) + v_ {3} ^ {2}) + v_ {3} ^ {2}) + v_ {2}} ^ {2} (w_ {1} ^ {2} + w_ {2} ^ {2} + w_ {3} ^ {2})\\ [4pt] &\ mathrel {\ fantasma {=}} {} - (v_ {1} ^ {2} w_ {1} ^ {2} + v_ {2} ^ {2} w_ {2} ^ {2}} + v_ {3} ^ {2} w_ {3} ^ {2} + 2 (v_ {1} w_ {1} v_ {2} w_ {2} + v_ {1} w_ {1} v_ {3} w_ {3} + v _ {2} w_ {2} v_ {3} w_ {3}))\\ [4pt] &= (v_ {1} ^ {2} + v_ {2} ^ {2} + v_ {3} ^ {2}) (w_ {1} ^ {2} + w_ {2} ^ {2} + w_ {3} ^ {2})\ [4pt] &\ mathrel {\ phantom {=}} {} - ((v_ {1} w_ {1}) ^ {2} + (v_ {2} w_ {2}) ^ {2} + (v_ {3} w_ {3}) ^ {2} + 2 (v_ {1} w_ {1}) (v_ {2} w_ {2}) + 2 (v_ {1} w_ {1}) (v_ {3} w_ {3}) + 2 (v_ {2} w_ {2}) (v_ {3} w_ {3}))\ end {alinear*}

por lo que el uso\((a + b + c)^{2} = a^{2} + b^{2} + c^{2} + 2ab + 2ac + 2bc\) para el término restado da

\ begin {alinear*} & = (v_ {1} ^ {2} + v_ {2} ^ {2} + v_ {3} ^ {2}) (w_ {1} ^ {2} + w_ {2} ^ {2} + w_ {3} ^ {2}) -
(v_ {1} w_ {1} + v_ {2} w_ {2} + v_ {2} w_ {2} + v_ {3} w_ {3}) ^ {2}\\ [4pt]
&=\ norma {\ textbf {v}} ^ {2}\,\ norma {\ textbf {w}} ^ {2} - (\ textbf {v}\ cdot\ textbf {w}) ^ {2}\\ [4pt]
&=\ norma {\ tbf {v}} ^ { 2}\,\ norma {\ textbf {w}} ^ {2}\ biggl (1 -
\ frac {(\ textbf {v}\ cdot\ textbf {w}) ^ {2}} {\ norma {\ textbf {v}} ^ {2}\,\ norma {\ textbf {w}} ^ {2}}\ biggr)
\ texto {, ya que\(\norm{\textbf{v}} > 0\) y\(\norm{\textbf{w}} > 0\), así por Teorema 1.6}\\ [4pt]
&=\ norm {\ textbf {v}} ^ {2}\,\ norm {\ textbf {w}} ^ {2} (1 -\ cos^ {2}\ theta)
\ text {, donde\(\theta\) esta el angulo entre\(\textbf{v}\) y\(\textbf{w}\), entonces}\\\ [4pt]
\ norm {\ textbf {v}\ times\ textbf {w}} ^ {2} &=\ norm {\ textbf {v}} ^ {2}\,\ norm {\ textbf {w}} ^ {2}\,\ sin^ {2}\ theta
\ text {, y desde\(0^{\circ} \le \theta \le 180^{\circ}\) entonces \(\sin \theta \ge 0\), entonces tenemos:}
\ end {align*}

Si\(\theta\) es el ángulo entre vectores distintos de cero\(\textbf{v}\) e\(\textbf{w}\) in\(\mathbb{R}^{3}\), entonces

\[\norm{\textbf{v} \times \textbf{w}} = \norm{\textbf{v}}\,\norm{\textbf{w}}\,\sin \theta \]

Puede parecer extraño molestarse con la fórmula anterior, cuando la magnitud del producto cruzado puede calcularse directamente, como para cualquier otro vector. La fórmula es más útil para sus aplicaciones en geometría, como en el siguiente ejemplo.

Ejemplo 1.8

Dejar\(\triangle PQR\) y\(PQRS\) ser un triángulo y un paralelogramo, respectivamente, como se muestra en la Figura 1.4.3.

Figura 1.4.3

Piense en el triángulo como existente en\(\mathbb{R}^{3}\), e identifique los lados\(QR\) y\(QP\) con vectores\(\textbf{v}\) y\(\textbf{w}\), respectivamente, en\(\mathbb{R}^{3}\). Dejar\(\theta\) ser el ángulo entre\(\textbf{v}\) y\(\textbf{w}\). El área\(A_{PQR}\) de\(\triangle PQR\) es\(\frac{1}{2} b h\), donde\(b\) está la base del triángulo y\(h\) es la altura. Entonces vemos que

\[\nonumber b = \norm{\textbf{v}} \text{ and } h = \norm{\textbf{w}}\,\sin \theta \]

\[\nonumber \begin{align} A_{PQR} &= \frac{1}{2}\,\norm{\textbf{v}}\,\norm{\textbf{w}}\,\sin \theta \\[4pt] \nonumber&= \frac{1}{2}\,\norm{\textbf{v} \times \textbf{w}} \\[4pt] \end{align}\]

Entonces como el área\(A_{PQRS}\) del paralelogramo\(PQRS\) es el doble del área del triángulo\(\triangle PQR\), entonces

\[\nonumber A_{PQRS} = \norm{\textbf{v}}\,\norm{\textbf{w}}\,\sin \theta\]

Por la discusión en el Ejemplo 1.8, hemos demostrado el siguiente teorema:

Teorema 1.13: Área de triángulos y paralelogramos

1. El área\(A\) de un triángulo con lados adyacentes\(\textbf{v}, \textbf{w}\) (como vectores en\(\mathbb{R}^{3}\)) es:
   \[\nonumber A = \frac{1}{2}\,\norm{\textbf{v} \times \textbf{w}}\]
2. El área\(A\) de un paralelogramo con lados adyacentes\(\textbf{v}, \textbf{w}\) (como vectores en\(\mathbb{R}^{3}\)) es:
   \[\nonumber A = \norm{\textbf{v} \times \textbf{w}}\]

Puede parecer a primera vista que dado que las fórmulas derivadas en el Ejemplo 1.8 fueron para los lados adyacentes\(QP\) y\(QR\) sólo, entonces no se justifican las declaraciones más generales en el Teorema 1.13 que las fórmulas tienen para lados\(\textit{any}\) adyacentes. Obtendríamos un diferente\(\textit{formula}\) para el área si hubiéramos escogido\(PQ\) y\(PR\) como los lados adyacentes, pero se puede demostrar (ver Ejercicio 26) que las diferentes fórmulas darían el mismo valor, por lo que la elección de lados adyacentes efectivamente no importa, y el Teorema 1.13 es válido.

El teorema 1.13 hace que sea más sencillo calcular el área de un triángulo en el espacio tridimensional que mediante el uso de métodos geométricos tradicionales.

Ejemplo 1.9

Calcular el área del triángulo\(\triangle PQR\), dónde\(P = (2,4,-7)\),\(Q = (3,7,18)\), y\(R =(-5,12,8)\).

Figura 1.4.4

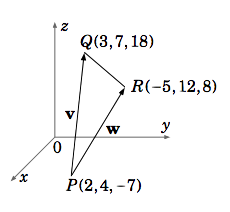
Solución

Dejar\(\textbf{v} = \overrightarrow{PQ}\) y\(\textbf{w} = \overrightarrow{PR}\), como en la Figura 1.4.4. Entonces\(\textbf{v} = (3,7,18) - (2,4,-7) = (1,3,25)\) y\(\textbf{w} = (-5,12,8) - (2,4,-7) = (-7,8,15)\), así el área\(A\) del triángulo\(\triangle PQR\) es

\ begin {align*}
A &=\ frac {1} {2}\,\ norm {\ textbf {v}\ veces\ textbf {w}} =\ frac {1} {2}\,\ norma {(1,3,25)\ veces (-7,8,15)}\\ [4pt]
&=\ frac {1} {2}\,\ norm {(3) (15) - (25) (8), (25) (-7) - (1) (15), (1) (8) - (3) (-7))}\\ [4pt]
&=\ frac {1} {2}\,\ norma {(-155, -190, 29)}\\ [4pt ]
&=\ frac {1} {2}\,\ sqrt {(-155) ^2 + (-190) ^2 + 29^2} =\ frac {1} {2}\,\ sqrt {60966}\\ [4pt]
A &\ aprox 123.46
\ end {align*}

Ejemplo 1.10

Calcular el área del paralelogramo\(PQRS\), dónde\(P = (1,1)\),\(Q = (2,3)\),\(R = (5,4)\), y\(S = (4,2)\).

Figura 1.4.5

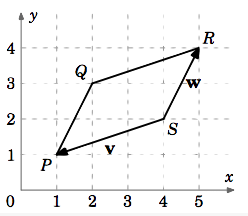
Solución

Dejar\(\textbf{v} = \overrightarrow{SP}\) y\(\textbf{w} = \overrightarrow{SR}\), como en la Figura 1.4.5. Entonces\(\textbf{v} = (1,1) - (4,2) = (-3,-1)\) y\(\textbf{w} = (5,4) - (4,2) = (1,2)\). Pero estos son vectores en\(\mathbb{R}^{2}\), y el producto cruzado solo se define para vectores en\(\mathbb{R}^{3}\). Sin embargo,\(\mathbb{R}^{2}\) puede pensarse como el subconjunto de\(\mathbb{R}^{3}\) tales que la\(z\) -coordenada es siempre\(0\). Para que podamos escribir\(\textbf{v} = (-3,-1,0)\) y\(\textbf{w} = (1,2,0)\). Entonces el área\(A\) de\(PQRS\) es

\ begin {align*}
A &=\ norm {\ textbf {v}\ times\ textbf {w}} =\ norm {(-3, -1,0)\ times (1,2,0)}\\ [4pt]
&=\ norm {((-1) (0) - (0) (2), (0) (1) - (-3) (0), (-3) (2) - (-1) (1))}\\ [4pt]
&=\ norm {(0,0, -5)}\\ [4pt]
A &= 5
\ end {alinear*}

El siguiente teorema resume las propiedades básicas del producto cruzado.

Teorema 1.14

Para cualquier vector\(\textbf{u}, \textbf{v}, \textbf{w}\) en\(\mathbb{R}^{3}\), y escalar\(k\), tenemos

1. \(\textbf{v} \times \textbf{w} = -\textbf{w} \times \textbf{v}\)Ley Anticonmutativa
2. \(\textbf{u} \times (\textbf{v} + \textbf{w}) = \textbf{u} \times \textbf{v} + \textbf{u} \times \textbf{w}\)Derecho Distributivo
3. \((\textbf{u} + \textbf{v}) \times \textbf{w} = \textbf{u} \times \textbf{w} + \textbf{v} \times \textbf{w}\)Derecho Distributivo
4. \((k\textbf{v}) \times \textbf{w} = \textbf{v} \times (k\textbf{w}) = k(\textbf{v} \times \textbf{w})\)Derecho asociativo
5. \(\textbf{v} \times \textbf{0} = \textbf{0} = \textbf{0} \times \textbf{v}\)
6. \(\textbf{v} \times \textbf{v} = \textbf{0}\)
7. \(\textbf{v} \times \textbf{w} = \textbf{0}\)si y solo si\(\textbf{v} \parallel \textbf{w}\)

Prueba

Las pruebas de propiedades (b) - (f) son sencillas. Demostraremos las partes (a) y (g) y dejaremos el resto al lector como ejercicios.

Figura 1.4.6

(a) Por la definición del producto cruzado y la multiplicación escalar, tenemos:
\ begin {align*}
\ textbf {v}\ times\ textbf {w} &= (v_ {2} w_ {3} - v_ {3} w_ {2},
v_ {3} w_ {1} - v_ {1} w_ {3}, v_ {1} _ {2} - v_ {2} w_ {1})\\ [4pt]
&= - (v_ {3} w_ {2} - v_ {2} w_ {3},
v_ {1} w_ {3} - v_ {3} w_ {1}, v_ {2} w_ {1} - v_ {1} w_ {2})\\ [4pt]
&= - (w_ {2} v_ {3} - w_ {3} v_ {2},
w_ {3} v_ {1} - _ {1} v_ {3}, w_ {1} v_ {2} - w_ {2} v_ {1})\\ [4pt]
&= -\ textbf {w}\ times\ textbf {v}
\ end {align*}
Tenga en cuenta que esto dice eso\(\textbf{v} \times \textbf{w}\) y\(\textbf{w} \times \textbf{v}\) tienen la misma magnitud pero dirección opuesta (ver Figura 1.4.6).

(g) Si cualquiera\(\textbf{v}\) o\(\textbf{w}\) es\(\textbf{0}\) entonces\(\textbf{v} \times \textbf{w} = \textbf{0}\) por la parte (e), y cualquiera\(\textbf{v} = \textbf{0} = 0\textbf{w}\) o\(\textbf{w} = \textbf{0} = 0\textbf{v}\), así\(\textbf{v}\) y\(\textbf{w}\) son múltiplos escalares, es decir, son paralelos.
Si ambos\(\textbf{v}\) y\(\textbf{w}\) son distintos de cero, y\(\theta\) es el ángulo entre ellos, entonces por la fórmula (1.11),\(\textbf{v} \times \textbf{w} = \textbf{0}\) si y solo si\(\norm{\textbf{v}}\,\norm{\textbf{w}}\,\sin \theta = 0\), que es verdadero si y solo si\(\sin \theta = 0\) (desde\(\norm{\textbf{v}} > 0\) y\(\norm{\textbf{w}} > 0)\). Entonces desde\(0^{\circ} \le \theta \le 180^{\circ}\), entonces\(\sin \theta = 0\) si y sólo si\(\theta = 0^{\circ}\) o\(180^{\circ}\). Pero el ángulo entre\(\textbf{v}\) y\(\textbf{w}\) es\(0^{\circ}\) o\(180^{\circ}\) si y sólo si\(\textbf{v} \parallel \textbf{w}\).

\(\square\)

Ejemplo 1.11

Añadiendo al Ejemplo 1.7, tenemos

\[\nonumber \textbf{i} \times \textbf{j} = \textbf{k},\quad \textbf{j} \times \textbf{k} = \textbf{i},\quad \textbf{k} \times \textbf{i} = \textbf{j}\]
\[\nonumber \textbf{j} \times \textbf{i} = -\textbf{k},\quad \textbf{k} \times \textbf{j} = -\textbf{i},\quad \textbf{i} \times \textbf{k} = -\textbf{j}\]
\[\nonumber \textbf{i} \times \textbf{i} = \textbf{j} \times \textbf{j} = \textbf{k} \times \textbf{k} = \textbf{0}\]

Recordemos de la geometría que a\(\textit{parallelepiped}\) es un sólido tridimensional con 6 caras, todas las cuales son paralelogramos.

Ejemplo 1.12

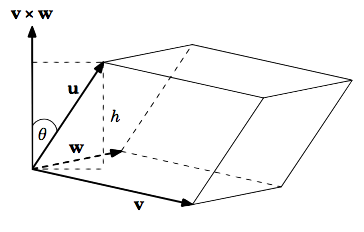
\(\textit{Volume of a parallelepiped:}\)Que los vectores\(\textbf{u}, \textbf{v}, \textbf{w}\) en\(\mathbb{R}^{3}\) representen lados adyacentes de un paralelepípedo\(P\), con la\(\textbf{u}, \textbf{v}, \textbf{w}\) formación de un sistema diestro, como en la Figura 1.4.7. Demostrar que el volumen de\(P\) es el\(\textit{scalar triple product}\)\(\textbf{u} \cdot (\textbf{v} \times \textbf{w})\).

Figura 1.4.7 Paralelepípedo\(P\)

Solución

Recordemos que el volumen\(\text{vol}(P)\) de un paralelepípedo\(P\) es el área\(A\) del paralelogramo base multiplicado por la altura\(h\). Por Teorema 1.13 (b), el área\(A\) del paralelogramo base es\(\norm{\textbf{v} \times \textbf{w}}\). Y podemos ver que ya que\(\textbf{v} \times \textbf{w}\) es perpendicular al paralelogramo base determinado por\(\textbf{v}\) y\(\textbf{w}\), entonces la altura\(h\) es\(\norm{\textbf{u}}\,\cos \theta\), donde\(\theta\) está el ángulo entre\(\textbf{u}\) y\(\textbf{v} \times \textbf{w}\). Por Teorema 1.6 sabemos que

\[\nonumber \begin{align} \cos \theta &= \dfrac{\textbf{u} \cdot (\textbf{v} \times \textbf{w})}{\norm{\textbf{u}} \, \norm{\textbf{v} \times \textbf{w}}}. \text{ Hence,} \\[4pt] \nonumber \text{vol}(P) &= A \, h \\[4pt] \nonumber&= \norm{\textbf{v} \times \textbf{w}} \, \dfrac{\norm{\textbf{u}} \, \textbf{u} \cdot (\textbf{v} \times \textbf{w})}{\norm{\textbf{u}} \,\norm{\textbf{v} \times \textbf{w}}} \\[4pt] \nonumber&= \textbf{u} \cdot (\textbf{v} \times \textbf{w}) \\[4pt] \end{align}\]

En el Ejemplo 1.12 la altura\(h\) del paralelepípedo es\(\norm{\textbf{u}}\,\cos \theta\), y no\(-\norm{\textbf{u}}\,\cos \theta\), porque el vector\(\textbf{u}\) está en el mismo lado del plano del paralelogramo base que el vector\(\textbf{v} \times \textbf{w}\) (así que\(\cos \theta > 0\)). Dado que el volumen es el mismo sin importar qué base y altura usemos, luego repitiendo los mismos pasos usando la base determinada por\(\textbf{u}\) y\(\textbf{v}\) (ya que\(\textbf{w}\) está en el mismo lado del
plano de esa base que\(\textbf{u} \times \textbf{v}\)), el volumen es\(\textbf{w} \cdot (\textbf{u} \times \textbf{v})\). Repitiendo esto con la base determinada por\(\textbf{w}\) y\(\textbf{u}\), tenemos el siguiente resultado:

Para cualquier vector\(\textbf{u}, \textbf{v}, \textbf{w}\) en\(\mathbb{R}^{3}\),

\[\textbf{u} \cdot (\textbf{v} \times \textbf{w}) = \textbf{w} \cdot (\textbf{u} \times \textbf{v}) = \textbf{v} \cdot (\textbf{w} \times \textbf{u})\label{Eq1.1.2}\]

(Tenga en cuenta que las igualdades se mantienen trivialmente si alguno de los vectores lo es\(\textbf{0}\).)

Ya que\(\textbf{v} \times \textbf{w} = -\textbf{w} \times \textbf{v}\) para cualquier vector\(\textbf{v}, \textbf{w}\) en\(\mathbb{R}^{3}\), luego elegir el orden incorrecto para los tres lados adyacentes en el producto triple escalar en la Ecuación\ ref {Eq1.1.2} le dará el negativo del volumen del paralelepípedo. Así que tomando el valor absoluto del producto triple escalar para cualquier orden de los tres lados adyacentes\(\textit{always}\) dará el volumen:

Teorema 1.15

Si los vectores\(\textbf{u}, \textbf{v}, \textbf{w}\) en\(\mathbb{R}^{3}\) representan tres lados adyacentes cualquiera de un paralelepípedo, entonces el volumen del paralelepípedo es\(|\textbf{u} \cdot (\textbf{v} \times \textbf{w})|\).

Otro tipo de producto triple es el\(\textit{vector triple product}\)\(\textbf{u} \times (\textbf{v} \times \textbf{w})\). La prueba del siguiente teorema se deja como ejercicio para el lector:

Teorema 1.16

Para cualquier vector\(\textbf{u}, \textbf{v}, \textbf{w}\) en\(\mathbb{R}^{3}\),

\[\textbf{u} \times (\textbf{v} \times \textbf{w}) = (\textbf{u} \cdot \textbf{w})\textbf{v} - (\textbf{u} \cdot \textbf{v})\textbf{w}\label{Eq1.13}\]

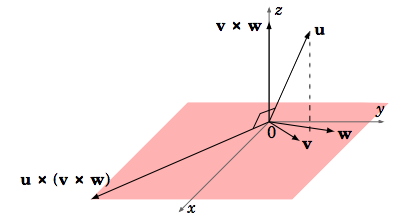
Un examen de la fórmula en el Teorema 1.16 da una idea de la geometría del producto triple del vector. Por el lado derecho de la Ecuación\ ref {Eq1.13}, vemos que\(\textbf{u} \times (\textbf{v} \times \textbf{w})\) es una combinación escalar de\(\textbf{v}\) y\(\textbf{w}\), y por lo tanto se encuentra en el plano que contiene\(\textbf{v}\) y\(\textbf{w}\) (es decir\(\textbf{u} \times (\textbf{v} \times \textbf{w})\),\(\textbf{v}\) y\(\textbf{w}\) son\(\textbf{coplanar}\)). Esto tiene sentido ya que, por el Teorema 1.11,\(\textbf{u} \times (\textbf{v} \times \textbf{w})\) es perpendicular a ambos\(\textbf{u}\) y\(\textbf{v} \times \textbf{w}\). En particular, al ser perpendicular a\(\textbf{v} \times \textbf{w}\) medios que\(\textbf{u} \times (\textbf{v} \times \textbf{w})\) se encuentran en el plano que contiene\(\textbf{v}\) y\(\textbf{w}\), ya que ese plano es en sí perpendicular a\(\textbf{v} \times \textbf{w}\). Pero entonces, ¿cómo es\(\textbf{u} \times (\textbf{v} \times \textbf{w})\) también perpendicular a\(\textbf{u}\), que podría ser cualquier vector? El siguiente ejemplo puede ayudar a ver cómo funciona esto.

Ejemplo 1.13

Encontrar\(\textbf{u} \times (\textbf{v} \times \textbf{w})\) para\(\textbf{u} = (1, 2, 4)\),\(\textbf{v} = (2, 2, 0)\),\(\textbf{w} = (1, 3, 0)\).

Solución

Desde\(\textbf{u} \cdot \textbf{v} = 6\) y\(\textbf{u} \cdot \textbf{w} = 7\), entonces

\ begin {align*}
\ textbf {u}\ times (\ textbf {v}\ times\ textbf {w}) &= (\ textbf {u}\ cdot\ textbf {w})\ textbf {v} - (\ textbf {u}\ cdot\ textbf {v})\ textbf {w}\ [4pt]
&= 7\, (2, 2, 0) - 6\, (1, 3, 0) = (14, 14, 0) - (6, 18, 0)\\ [4pt]
&= (8, -4, 0)
\ end { alinear*}

Obsérvese eso\(\textbf{v}\) y\(\textbf{w}\) yace en el\(xy\) -plano, y eso\(\textbf{u} \times (\textbf{v} \times \textbf{w})\) también se encuentra en ese plano. Además,\(\textbf{u} \times (\textbf{v} \times \textbf{w})\) es perpendicular a ambos\(\textbf{u}\) y\(\textbf{v} \times \textbf{w} = (0, 0, 4)\) (ver Figura 1.4.8).

Figura 1.4.8

Para vectores\(\textbf{v} = v_{1}\textbf{i} + v_{2}\textbf{j} + v_{3}\textbf{k}\) y\(\textbf{w} = w_{1}\textbf{i} + w_{2}\textbf{j} + w_{3}\textbf{k}\) en forma de componentes, el producto cruzado se escribe como:\(\textbf{v} \times \textbf{w} = (v_{2}w_{3} - v_{3}w_{2})\textbf{i} + (v_{3}w_{1} - v_{1}w_{3})\textbf{j} + (v_{1}w_{2} - v_{2}w_{1})\textbf{k}\). A menudo es más fácil usar la forma de componente para el producto cruzado, ya que se puede representar como un\(\textit{determinant}\). No vamos a adentrarnos demasiado en la teoría de los determinantes; solo cubriremos lo que es esencial para nuestros propósitos.

Una matriz\(\times\) 2 2} es una matriz de dos filas y dos columnas de escalares, escrita como

\[\nonumber \begin{bmatrix}a & b\\[4pt]c & d\end{bmatrix} \text{or} \begin{pmatrix}a & b\\[4pt]c & d\end{pmatrix}\]

donde\(a, b, c, d\) están los escalares. El\(\textbf{determinant}\) de tal matriz, escrito como

\[\nonumber \begin{vmatrix}a & b\\[4pt]c & d\end{vmatrix} \text{or} \det \begin{bmatrix}a & b\\[4pt]c & d\end{bmatrix},\]

es el escalar definido por la siguiente fórmula:

\[\nonumber \begin{vmatrix}a & b\\[4pt]c & d\end{vmatrix}= ad - bc\]

Puede ser útil recordar esta fórmula como producto de los escalares en la diagonal descendente menos el producto de los escalares en la diagonal ascendente.

Ejemplo 1.14

\[\nonumber \begin{vmatrix}1 & 2\\[4pt]3 & 4\end{vmatrix} = (1)(4) - (2)(3) = 4 - 6 = -2\]

Una\(3 \times 3\) matriz es una matriz de tres filas y tres columnas de escalares, escrita como

\ [\ nonumber\ begin {bmatrix} a_ {1} & a_ {2} & a_ {3}\\ [4pt]
b_ {1} & b_ {2} & b_ {3}\\ [4pt]
c_ {1} & c_ {2} & c_ {3}
\ end {bmatrix}
\ text {o}
\ begin {pmatrix} a_ {1} y a_ {2} y a_ {3}\\ [4pt]
b_ {1} y b_ {2} & b_ {3}\\ [4pt]
c_ {1} & c_ {2} & c_ {3}
\ end {pmatrix}, $$
y su determinante viene dado por la fórmula:
\ [\ begin {vmatrix} a_ {1} & a_ {2} & a_ {3}\\ [4pt]
b_ {1} & b_ {2} & b_ {3}}\\ [4pt]
c_ {1} & c_ {2} & amp; c_ {3}
\ end {vmatrix}
= a_ {1}\ begin {vmatrix} b_ {2} & b_ {3}\\ [4pt] c_ {2} & c_ {3}\ end {vmatrix}\; -\;
a_ {2}\ begin {vmatrix} b_ {1} & b_ {3}\\ [4pt] {1} & c_ {3}\ end {vmatrix}\; +\;
a_ {3}\ begin {vmatrix} b_ {1} & b_ {2}\ \[4pt] c_{1} & c_{2} \end{vmatrix}\]

Una forma de recordar la fórmula anterior es la siguiente: multiplicar cada escalar en la primera fila por el determinante de la\(2 \times 2\) matriz que queda después de eliminar la fila y columna que contienen ese escalar, luego sumar esos productos, poniendo alternando signos más y menos delante de cada uno (comenzando con un más).

Ejemplo 1.15

\ [\ nonumber\ izquierda|\ begin {array} {rrr} 1 & 0 & 2\\ [4pt] 4 & -1 & 3\\ [4pt] 1 & 0 & 2\ end {array}\ derecha|
= 1\ izquierda|\ begin {array} {rr} -1 & 3\\ [4pt] 0 & 2\ end {array}\ derecha|\; -\;
0\ izquierda|\ begin {array} {rr} 4 & 3\\ [4pt] 1 & 2\ end {array}\ derecha|\; +\;
2\ izquierda|\ begin {array} {rr} 4 & -1\\ [4pt] 1 & 0\ end {array}\ derecha|
= 1 (-2 - 0) - 0 (8 - 3) + 2 (0 + 1) = 0\]

Definimos el determinante como un escalar, derivado de operaciones algebraicas sobre entradas escalares en una matriz. No obstante, si ponemos tres\(\textit{vectors}\) en la primera fila de una\(3 \times 3\) matriz, entonces la definición todavía tiene sentido, ya que estaríamos realizando multiplicación escalar en esos tres vectores (se multiplicarían por los determinantes\(2 \times 2\) escalares como antes). Esto nos da un determinante que ahora es un vector, y nos permite escribir el producto cruzado de\(\textbf{v} = v_{1}\textbf{i} + v_{2}\textbf{j} + v_{3}\textbf{k}\) y\(\textbf{w} = w_{1}\textbf{i} + w_{2}\textbf{j} + w_{3}\textbf{k}\) como determinante:

\ begin {align*}
\ nonumber\ textbf {v}\ times\ textbf {w} =
\ begin {vmatrix}\ textbf {i} &\ textbf {j} &\ textbf {k}\\ [4pt] v_ {1} & v_ {2} & v_ {3}\\ [4pt]
w_ {1} & w_ {2} & w_ {3}
\ end {vmatrix} &=\ begin {vmatrix} v_ {2} & v_ {3}\\ [4pt] w_ {2} & w_ {3}\ end {vmatrix}\ textbf {i}\; -\;
\ begin {vmatrix} v_ {1} & v_ {3}\\ [4pt] w_ {1} & w_ {3}\ end {vmatrix}\ textbf {j}\; +\;
\ begin {vmatrix} v_ {1} & _ {2}\\ [4pt] w_ {1} & w_ {2}\ end {vmatrix}\ textbf {k}\\ [4pt]\ nonumber
&= (v_ {2} w_ {3} - v_ {3} w _ {2})\ textbf {i} + (v_ {3} w_ {1} - v_ {1} w_ {3})\ textbf {j} +
(v_ {1} w_ {2} - v_ {2} w_ {1})\ textbf {k}
\ end {align*}

Ejemplo 1.16

Dejar\(\textbf{v} = 4\,\textbf{i} - \textbf{j} + 3\,\textbf{k}\) y\(\textbf{w} = \textbf{i} + 2\,\textbf{k}\). Entonces

\ [\ nonumber\ textbf {v}\ times\ textbf {w} =
\ izquierda|\ begin {array} {rrr}
\ textbf {i} &\ textbf {j} &\ textbf {k}\\ [4pt]
4 & -1 & 3\\ [4pt]
1 & 0 & 2
\ end {array}\ derecha|
=\ izquierda|\ begin {array} {rr} -1 & 3\\ [4pt] 0 & 2\ end {array}\ derecha|\ textbf {i}\; -\;
\ izquierda|\ begin {array} {rr} 4 & 3\\ [4pt] 1 & 2\ end {array}\ derecha|\ textbf {j}\; +\;
\ izquierda|\ begin array} {rr} 4 & -1\\ [4pt] 1 & 0\ end {array}\ derecha|\ textbf {k}
= -2\,\ textbf {i} - 5\,\ textbf {j} +\ textbf {k}\]

El producto triple escalar también se puede escribir como determinante. De hecho, por el Ejemplo 1.12, el siguiente teorema proporciona una definición alternativa del determinante de una\(3 \times 3\) matriz como el volumen de un paralelepípedo cuyos lados adyacentes son las filas de la matriz y forman un sistema diestro (un sistema zurdo daría el volumen negativo).

Teorema 1.17

 

Para cualquier vector\(\textbf{u} = (u_{1}, u_{2}, u_{3})\),\(\textbf{v} = (v_{1}, v_{2}, v_{3})\),\(\textbf{w} = (w_{1}, w_{2}, w_{3})\) en\(\mathbb{R}^{3}\):
\ [\ textbf {u}\ cdot (\ textbf {v}\ times\ textbf {w}) =
\ begin {vmatrix} u_ {1} & u_ {2} & u_ {3}\\ [4pt]
v_ {1} & v_ {2} & v_ {3}\\ [4pt]
w_ {1}} & w_ {2} & w_ {3}
\ end {vmatrix}\]

Ejemplo 1.17

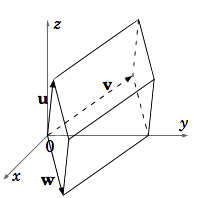
Encuentra el volumen del paralelepípedo con lados adyacentes\(\textbf{u} = (2, 1, 3)\),\(\textbf{v} = (-1, 3, 2)\),\(\textbf{w} = (1, 1, -2)\) (ver Figura 1.4.9).

Figura 1.4.9\(P\)

Solución

Por Teorema 1.15, el volumen\(\text{vol}(P)\) del paralelepípedo\(P\) es el valor absoluto del producto triple escalar de los tres lados adyacentes (en cualquier orden). Por Teorema 1.17,

\ begin {align*}
\ nonumber\ textbf {u}\ cdot (\ textbf {v}\ times\ textbf {w}) &=
\ izquierda|\ begin {array} {rrr}
2 & 1 & 3\\ [4pt]
-1 & 3 & 2\\ [4pt]
1 & 1 &-2
\ end {array}\ derecha|\\ [4pt]\ nonúmero
&= 2\ izquierda|\ begin {array} {rr} 3 & 2\\ [4pt] 1 & -2\ end {array}\ derecha|\; -\;
1\ izquierda|\ begin {array} {rr} -1 & 2\\ [4pt] 1 & -2\ end {array}\ derecha|\; +\;
3\ izquierda|\ begin {array} {rr} -1 & 3\\ [4pt] 1 & 1\ end {array}\ derecha|\\ [4pt]\ nonumber
& ; = 2 (-8) - 1 (0) + 3 (-4) = -28\ texto {, entonces}\\\ [4pt]\ nonúmero
\ texto {vol} (P) &= |-28| = 28.
\ end {alinear*}

Intercambiar los productos de punto y cruz puede ser útil para probar identidades vectoriales:

Ejemplo 1.18

Demostrar:\ (\ textbf {u}\ veces\ textbf {v})\ cdot (\ textbf {w}\ veces\ textbf {z}) =
\ begin {vmatrix}
\ textbf {u}\ cdot\ textbf {w} &\ textbf {u}\ cdot\ textbf {z}\\ [4pt]
\ tbf f {v}\ cdot\ textbf {w} &\ textbf {v}\ cdot\ textbf {z}\ end {vmatrix}\) para todos los vectores\ (\ textbf {u} ,
\ textbf {v},\ textbf {w},\ textbf {z}\) en\(\mathbb{R}^{3}\).

Solución

Vamos\(\textbf{x} = \textbf{u} \times \textbf{v}\). Entonces

\ begin {align*}
(\ textbf {u}\ veces\ textbf {v})\ cdot (\ textbf {w}\ veces\ textbf {z}) &=
\ textbf {x}\ cdot (\ textbf {w}\ veces\ textbf {z})\\ [4pt]
&=\ textbf {w}\ cdot (\ textbf {z}\ times\ textbf {x})\ text {(por Ecuación\ ref {Eq1.1.2})}\\ [4pt]
&=\ textbf {w}\ cdot (\ textbf {z}\ times (\ textbf {u}\ veces\ textbf {v}))\\ [4pt]
&=\ textbf {w}\ cdot ((\ textbf {z}\ cdot\ textbf {v})\ textbf {u} -
(\ textbf {z}\ punto\ textbf {u})\ textbf {v})\ text {(por Teorema 1.16)}\\ [4pt]
&= (\ textbf {z}\ cdot\ textbf {v}) (\ textbf {w}\ cdot\ textbf {u}) -
(\ textbf {z}\ cdot\ textbf {u}) (\ textbf {w}\ cdot\ textbf {v})\\ [4pt]
&= (\ textbf {u}\ cdot\ textbf {w}) (\ textbf {v}\ cdot\ textbf {z}) -
(\ textbf {u}\ cdot\ textbf {z}) (\ textbf {v}\ cdot\ textbf {w})\ text {(por conmutatividad del producto punto).}\\ [4pt]
&=\ begin {vmatrix}
\ textbf {u}\ cdot\ textbf {w} &\ textbf {u}\ cdot\ textbf {z}\\ [4pt]
\ textbf {v}\ cdot\ textbf {w} &\ textbf {v}\ cdot\ textbf {z}\ end {vmatrix}
\ end align{ *}

Colaboradores y Atribuciones

• Template:ContribCorral