2.5: Regresión

Ya hemos visto ejemplos en el texto donde se utilizan funciones lineales y cuadráticas para modelar una amplia variedad de fenómenos del mundo real que van desde los costos de producción hasta la altura de un proyectil sobre el suelo. En esta sección, utilizamos algunas herramientas básicas del análisis estadístico para cuantificar tendencias lineales y cuadráticas que podemos ver en datos del mundo real con el fin de generar modelos lineales y cuadráticos. Nuestro objetivo es dar al lector una comprensión de los procesos básicos involucrados, pero nos apresuramos a referir al lector a un curso más avanzado ¹ para una exposición completa de este material. Supongamos que recolectamos tres puntos de datos:$\{(1,2), (3,1), (4,3)\}$. Al trazar estos puntos, podemos ver claramente que no se encuentran en la misma línea. Si elegimos cualquiera de los dos puntos, podemos encontrar una línea que contenga ambos que pierda por completo el tercero, pero nuestro objetivo es encontrar una línea que en cierto sentido esté 'cerca' de todos los puntos, aunque pueda pasar por ninguno de ellos. La forma en que medimos la 'cercanía' en este caso es encontrar el error cuadrado total entre los puntos de datos y la línea. Considera nuestros tres puntos de datos y la línea$y=\frac{1}{2}x + \frac{1}{2}$. Para cada uno de nuestros puntos de datos, encontramos la distancia vertical entre el punto y la línea. Para lograr esto, necesitamos encontrar un punto en la línea directamente encima o debajo de cada punto de datos, es decir, un punto en la línea con la misma$x$ coordenada que nuestro punto de datos. Por ejemplo, para encontrar el punto en la línea directamente abajo$(1,2)$, nos$x=1$ conectamos$y=\frac{1}{2}x + \frac{1}{2}$ y obtenemos el punto$(1,1)$. De igual manera, llegamos$(3,1)$ a corresponder a$(3,2)$ y$\left(4,\frac{5}{2} \right)$ para$(4,3)$.

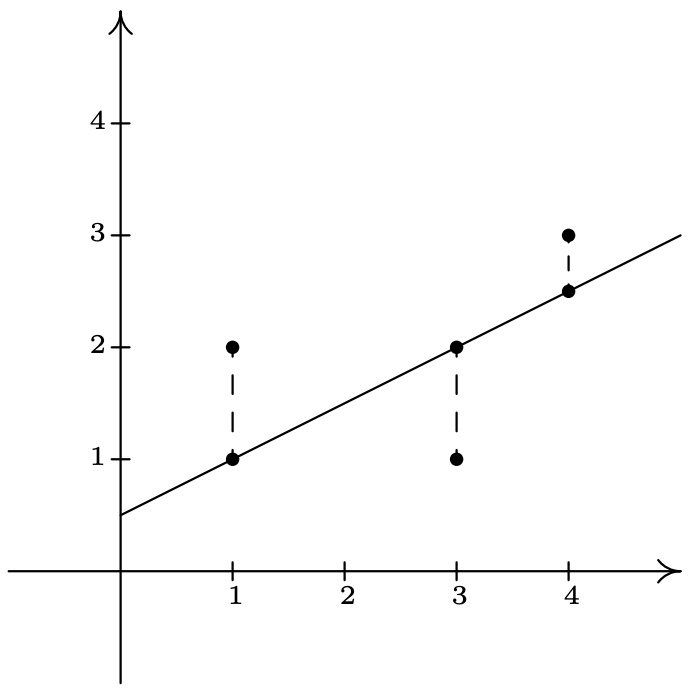
Encontramos el error cuadrado total$E$ tomando la suma de los cuadrados de las diferencias de las$y$ coordenadas de cada punto de datos y su punto correspondiente en la línea. Para los datos y la línea anterior$E = (2-1)^2+(1-2)^2+\left(3-\frac{5}{2}\right)^2 = \frac{9}{4}$. Utilizando maquinaria matemática avanzada, ² es posible encontrar la línea que da como resultado el valor más bajo de$E$. Esta línea se llama la línea de regresión de mínimos cuadrados, o a veces la 'línea de mejor ajuste'. La fórmula para la línea de mejor ajuste requiere notación que no presentaremos hasta el Capítulo 9.1, por lo que volveremos a visitarla entonces. La calculadora gráfica puede venir a nuestra ayuda aquí, ya que tiene una función incorporada para calcular la línea de regresión. Ingresamos los datos y realizamos la función de Regresión Lineal y obtenemos

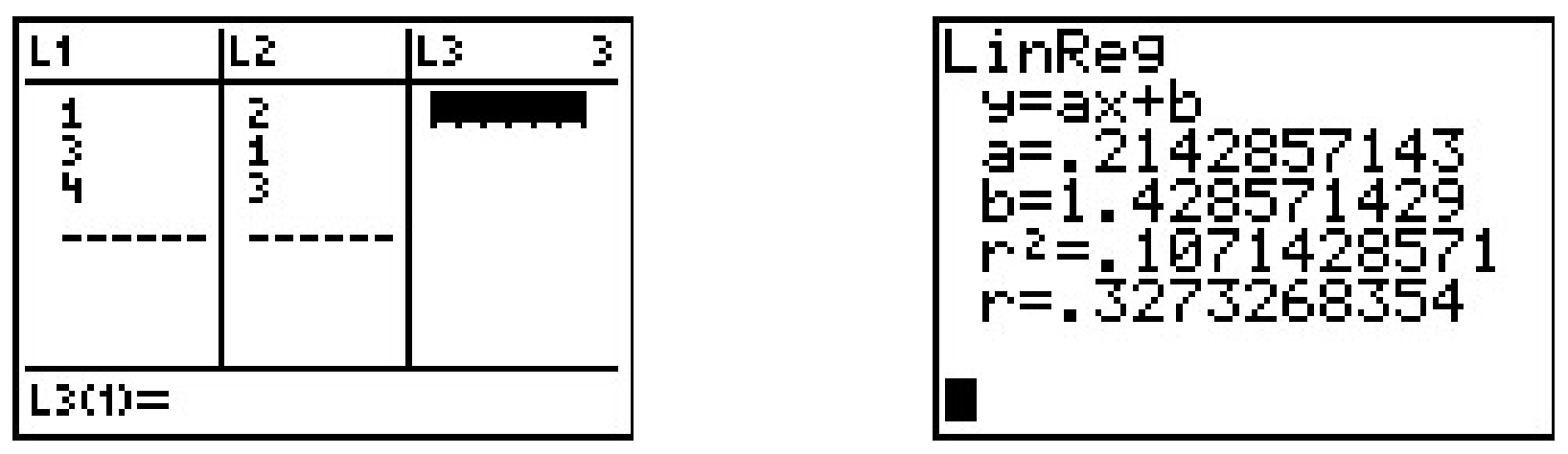
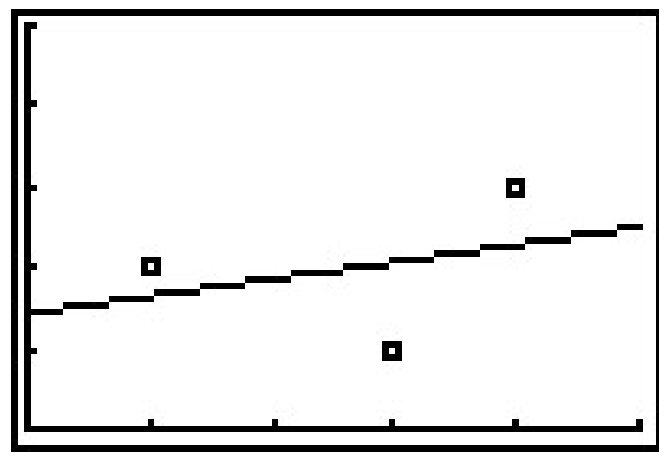
La calculadora nos dice que la línea de mejor ajuste es$y=ax+b$ donde está la pendiente$a \approx 0.214$ y la$y$ coordenada -de la$y$ -intercepción está$b \approx 1.428$. (Nos ceñiremos a usar tres decimales para nuestras aproximaciones.) Usando esta línea, calculamos el error cuadrado total para que nuestros datos sean$E \approx 1.786$. El valor$r$ es el coeficiente de correlación y es una medida de lo cerca que están los datos de estar en la misma línea. Cuanto más cerca$|r|$ está$1$, mejor es el ajuste lineal. Ya que$r \approx 0.327$, esto nos dice que la línea de mejor ajuste no encaja tan bien, en otras palabras, nuestros puntos de datos no están cerca de ser lineales. El valor$r^2$ se llama coeficiente de determinación y también es una medida de la bondad de ajuste. ³ Trazar los datos con su línea de regresión resulta en la siguiente imagen.

Nuestro primer ejemplo analiza el consumo de energía en Estados Unidos durante los últimos 50 años. ⁴

Año	Uso de Energía, en Quads ^5
1950	34.6
1960	45.1
1970	67.8
1980	78.3
1990	84.6
2000	98.9

Ejemplo 2.5.1

Utilizando los datos de consumo de energía indicados anteriormente,

1. Trazar los datos usando una calculadora gráfica.
2. Encuentra la línea de regresión de mínimos cuadrados y comenta la bondad de ajuste.
3. Interpretar la pendiente de la línea de mejor ajuste.
4. Utilice la línea de regresión para predecir el consumo anual de energía de Estados Unidos en el año$2013$.
5. Utilice la línea de regresión para predecir cuándo llegará el consumo anual a$120$ Quads.

Solución

1. Ingresar los datos en la calculadora da

   

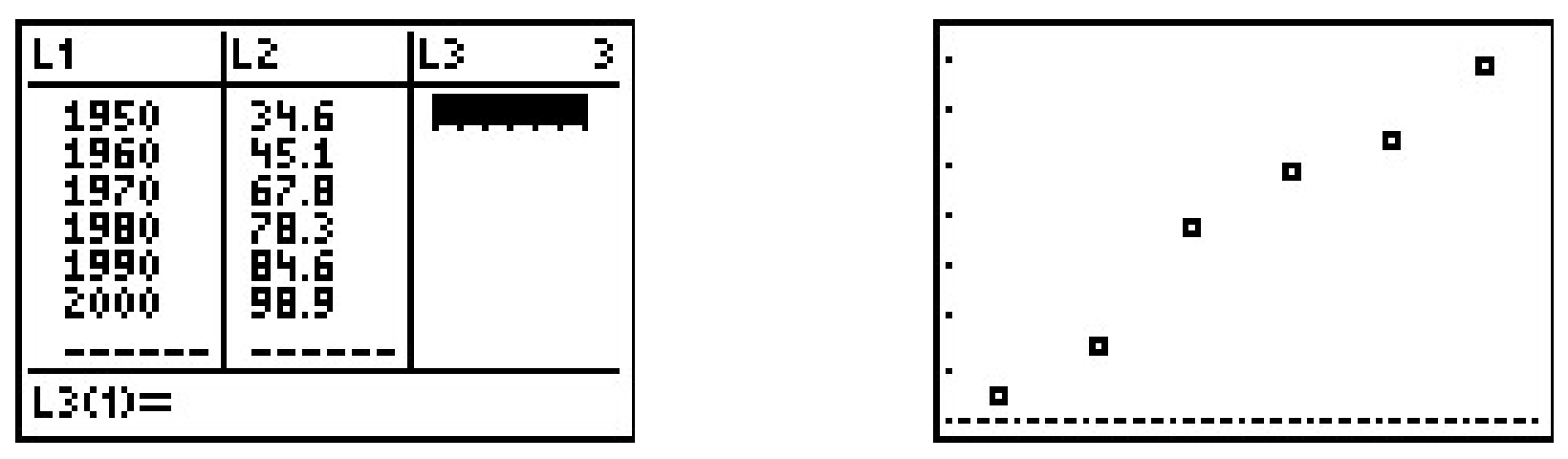
   Los datos ciertamente parecen ser de naturaleza lineal.

2. Realizar una regresión lineal produce

   

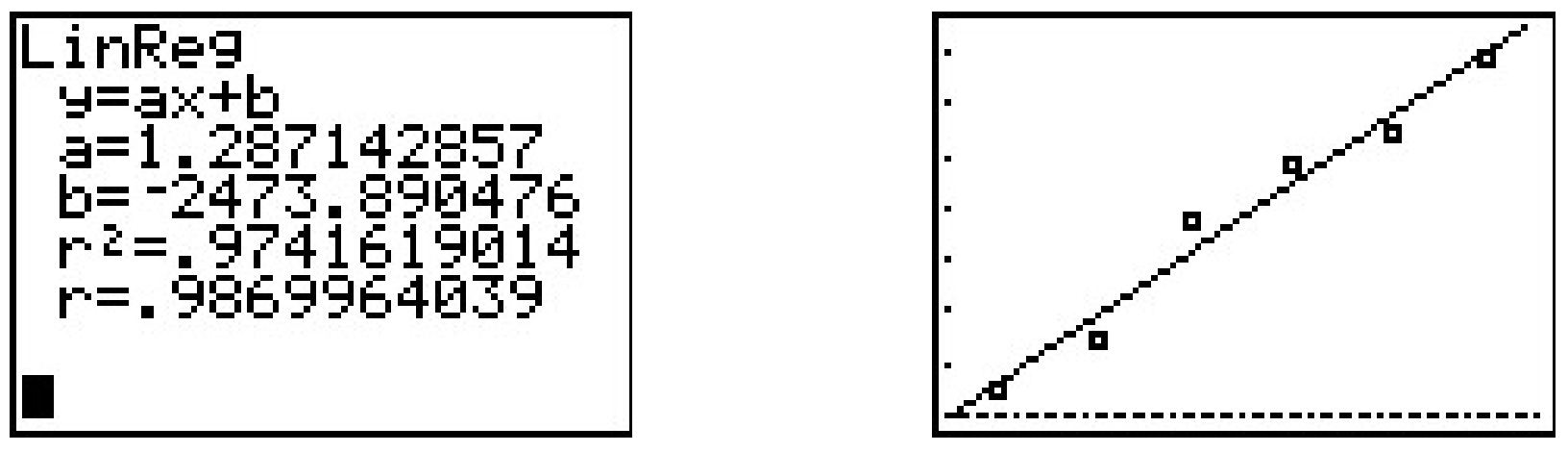
   Podemos decir tanto del coeficiente de correlación como de la gráfica que la línea de regresión es un buen ajuste a los datos.

3. La pendiente de la línea de regresión es$a \approx 1.287$. Para interpretar esto, recordemos que la pendiente es la tasa de cambio$y$ de las coordenadas con respecto a las$x$ coordenadas. Dado que las$y$ coordenadas representan el uso de energía en Quads, y las$x$ coordenadas representan años, una pendiente de positivo$1.287$ indica un aumento en el uso anual de energía a la tasa de$1.287$ Quads por año.
4. Para predecir las necesidades energéticas en$2013$, sustituimos$x=2013$ en la ecuación de la línea de mejor ajuste para obtener$y = 1.287(2013)-2473.890 \approx 116.841$. El uso anual de energía previsto de Estados Unidos en$2013$ es aproximadamente$116.841$ Quads.
5. Para predecir cuándo llegará el consumo anual de energía de Estados Unidos a$120$ Quads, sustituimos$y=120$ en la ecuación de la línea de mejor ajuste para obtener$120 = 1.287x - 2473.908$. Resolviendo$x$ rendimientos$x \approx 2015.454$. Dado que la línea de regresión va en aumento, interpretamos este resultado como diciendo que el uso anual en aún$2015$ no será$120$ Quads, pero que en$2016$, la demanda será más que$120$ Quads.

Nuestro siguiente ejemplo nos da la oportunidad de encontrar un modelo no lineal que se ajuste a los datos. De acuerdo con el Servicio Meteorológico Nacional, las temperaturas horarias previstas para Painesville el 3 de marzo de 2009 se dieron como se resume a continuación.

$\begin{array}{|c|c|} \hline \mbox{Time} & \mbox{Temperature, $^{\circ}$F} \\ \hline 10 \mbox{AM} & 17 \\ \hline 11 \mbox{AM} & 19 \\ \hline 12 \mbox{PM} & 21 \\ \hline 1 \mbox{PM} & 23 \\ \hline 2 \mbox{PM} & 24 \\ \hline 3 \mbox{PM} & 24 \\ \hline 4 \mbox{PM} & 23 \\ \hline \end{array}$

Para ingresar estos datos en la calculadora, necesitamos ajustar los$x$ valores, ya que solo ingresar los números podría causar confusión. (¿Ves por qué?) Tenemos algunas opciones disponibles para nosotros. Quizás lo más fácil es convertir los tiempos en el tiempo del reloj de 24 horas para que$1$ PM sea$13$,$2$ PM es$14$, etc. Si ingresamos estos datos en la calculadora gráfica y trazamos los puntos obtenemos

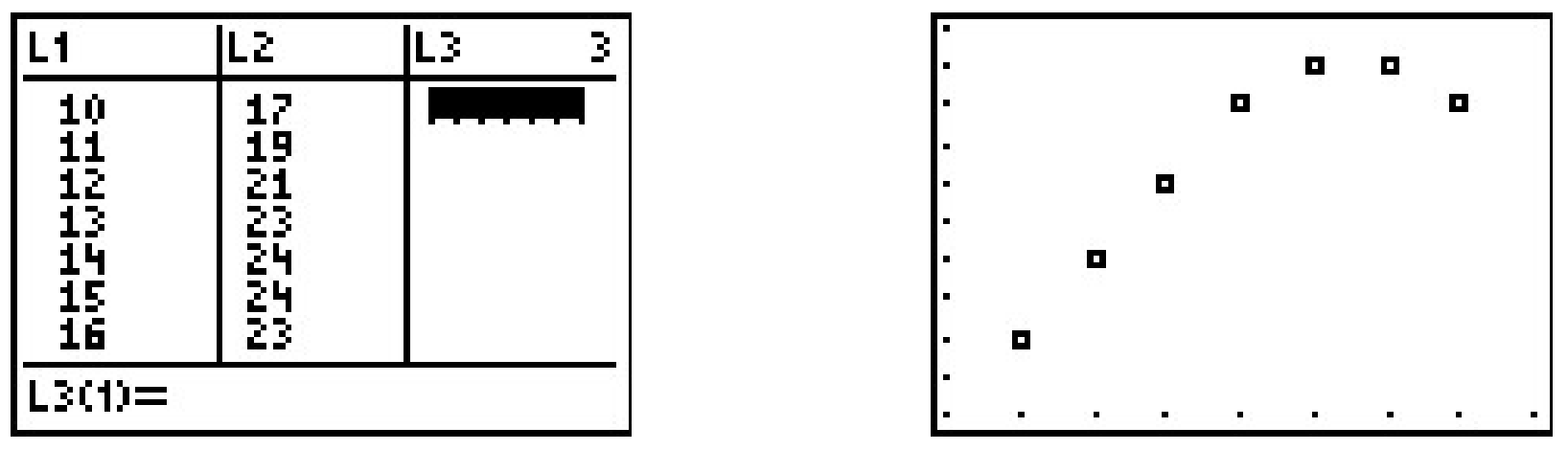
Si bien el inicio de los datos parece lineal, la temperatura comienza a bajar en las horas de la tarde. Este tipo de comportamiento nos recuerda a las parábolas, y, efectivamente, es posible encontrar una parábola de mejor ajuste de la misma manera que encontramos una línea de mejor ajuste. El proceso se denomina regresión cuadrática y su objetivo es minimizar el error de mínimos cuadrados de los datos con sus puntos correspondientes en la parábola. La calculadora también tiene una función incorporada para esto que rinde

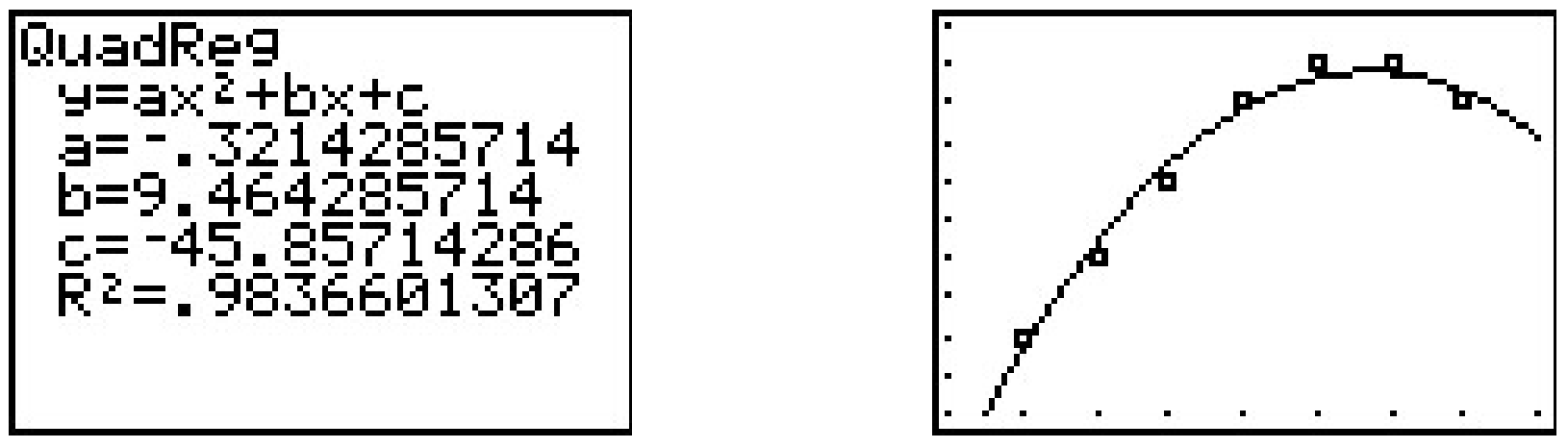
El coeficiente de determinación$R^2$ parece razonablemente cercano$1$, y la gráfica visualmente parece ser un ajuste decente. Utilizamos este modelo en nuestro siguiente ejemplo.

Ejemplo 2.5.2

Usando el modelo cuadrático para los datos de temperatura anteriores, predice la temperatura más cálida del día. ¿Cuándo ocurrirá esto?

Solución

La temperatura máxima ocurrirá en el vértice de la parábola. Recordando la Fórmula Vertex, Ecuación 2.4,$x = -\frac{b}{2a} \approx - \frac{9.464}{2(-0.321)} \approx 14.741$. Esto corresponde aproximadamente a$2\!:\!45$ PM. Para encontrar la temperatura, sustituimos$x = 14.741$ en$y = -0.321 x^2+9.464x - 45.857$ para obtener$y \approx 23.899$, o$23.899^{\circ}$ F.

Los resultados del último ejemplo deberían recordarte que los modelos de regresión son solo eso, modelos. Se encontró que nuestra temperatura más cálida predicha era$23.899^{\circ}$ F, pero nuestros datos dicen que se calentará a$24^{\circ}$ F. Está muy bien observar tendencias y adivinar un modelo, pero una investigación más profunda sobre por qué ciertos datos deben ser de naturaleza lineal o cuadrática suele estar en orden - y que, la mayoría de las veces, es asunto de los científicos.

2.5.1 Ejercicios

1. Según este sitio web ⁶, los datos censales del condado de Lake, Ohio son:

   \ (\\ begin {array} {|l|r|r|r|r|}
   \ hline\ text {Año} & 1970 & 1980 & 1990 & 2000\
   \ hline\ text {Población} & 197200 & 212801 & 215499 & 227511\
   \ hline
   \ end {array}\)

   1. Encuentra la línea de regresión de mínimos cuadrados para estos datos y comenta la bondad de ajuste. ⁷ Interpretar la pendiente de la línea de mejor ajuste.
   2. Utilice la línea de regresión para predecir la población del condado de Lake en 2010. (La cifra registrada del censo de 2010 es$230,\!041$)
   3. Utilice la línea de regresión para predecir cuándo llegará la población del condado de Lake$250,\!000$.
2. Según este sitio web ⁸, los datos del censo del condado de Lorain, Ohio son:

   \ (\\ begin {array} {|l|r|r|r|r|}
   \ hline\ text {Año} & 1970 & 1980 & 1990 & 2000\
   \ hline\ text {Población} & 256843 & 274909 & 271126 & 284664\
   \ hline
   \ end {array}\)

   1. Encuentra la línea de regresión de mínimos cuadrados para estos datos y comenta la bondad de ajuste. Interpretar la pendiente de la línea de mejor ajuste.
   2. Utilizar la línea de regresión para predecir la población del condado de Lorain en 2010. (La cifra registrada del censo de 2010 es$301,\!356$)
   3. Utilice la línea de regresión para predecir cuándo llegará la población del condado de Lake$325,\!000$.
3. Usando los datos de producción de energía dados a continuación

   \ (\\ begin {array} {|l|l|l|l|l|l|l|l|}
   \ hline\ text {Año} & 1950 & 1960 & 1970 & 1980 & 1990 & 2000\
   \ hline\ text {Producción} & & & & & & &\
   \ texto {(en Quads)} & 35.6 & 42.8 & 63.5 & 67.2 & 70.7 & 71.2\\
   \ hline
   \ end {array}\)

   1. Trace los datos usando una calculadora gráfica y explique por qué no parece ser lineal.
   2. Discuta con sus compañeros de clase por qué ignorar los dos primeros puntos de datos puede justificarse desde una perspectiva histórica.
   3. Encuentra la línea de regresión de mínimos cuadrados para los últimos cuatro puntos de datos y comenta la bondad de ajuste. Interpretar la pendiente de la línea de mejor ajuste.
   4. Utilice la línea de regresión para predecir la producción anual de energía de Estados Unidos en el año$2010$.
   5. Utilice la línea de regresión para predecir cuándo llegará la producción anual de energía de Estados Unidos a$100$ Quads.
4. El siguiente cuadro contiene una parte de la información de consumo de combustible de un Toyota Echo 2002 que yo (Jeff) solía poseer. La primera fila es el número acumulado de galones de gasolina que había usado y la segunda fila es la lectura del odómetro cuando rellené el tanque de gasolina. Entonces, por ejemplo, la cuarta entrada es el punto (28.25, 1051) que dice que había usado un total de 28.25 galones de gasolina cuando el odómetro leía 1051 millas.

   \ (\\ begin {array} {|l|r|c|c|c|c|c|c|c|c|c|c|c|}
   \ hline\ begin {array} {l}
   \ text {Gasolina Usada}
   \\ texto {(Galones)}
   \ end {array} & 0 & 9.26 & 19.03 & 28.25 & 36.45 & 44.64 & 53.57 & 62.62 y 71.93 & 81.69 & 90.43\
   \ hline\ begin {array} {l}
   \ text {odómetro}\
   \ text {(Millas)}
   \ end {array} & 41 & 356 & 731 & 1051 & 1347 & 1631 & 1966 & 2310 & 2670 & 3030 & 3371\
   \ hline
   \ end {array}\)

   Encuentra la línea de mínimos cuadrados para estos datos. ¿Es un buen ajuste? ¿Qué representa la pendiente de la línea? ¿Tú y tus compañeros creen que este modelo se habría mantenido durante diez años si no hubiera estrellado el auto en la Turnpike hace unos años? (Estoy guardando un registro de combustible para mi Scion xA 2006 para futuros libros de Álgebra Universitaria, así que espero no estrellarlo también).

5. El día de Año Nuevo, yo (Jeff, de nuevo) comencé a pesarme todas las mañanas para tener un interesante conjunto de datos para esta sección del libro. (Discuta con tus compañeros de clase si eso me convierte en un nerd o un geek. Además, los profesionales en el campo del control de peso desalientan fuertemente pesarse cada día. Cuando te enfocas en el número y no en tu salud general, tiendes a perder de vista tus objetivos. Estaba haciendo un noble sacrificio por la ciencia, pero deberías probar esto en casa.) Todo el gráfico sería demasiado grande para ponerlo en el libro pulcramente, así que he decidido darle solo una pequeña porción de los datos a usted. Esto se convierte entonces en una lección cívica de honestidad, como pronto verás. A continuación se indican dos gráficos. Uno tiene mi peso para los primeros ocho jueves del año (el 1 de enero de 2009 fue jueves y lo contaremos como Día 1.) y el otro tiene mi peso para los primeros 10 sábados del año.

   \ (\\ begin {aligned}
   &\ begin {array} {|l|r|r|r|r|r|r|r|r|r|r|}
   \ hline\ begin {array} {l}
   \ text {día #}
   \\ texto {(jueves)}
   \ end {array} & 1 & 8 & 15 & 22 & 29 y 36 & 43 & 50\\
   \ hline\ begin {array} {l}
   \ text {Mi peso}\\
   \ text {en libras}
   \ end {array} & 238.2 & 237.0 & 235.6 & 234.4 & 233.0 & 233.8 & 232.8 & 232.0\
   \ hline
   \ end {array}\\
   &\ begin {array} {|l|r|r|r|r|r|r|r|r|r|r|r|r|}
   \ hline\ begin {array} {l}
   \ text {día #}
   \\ texto {(sábado)}
   \ end {array} & 3 & 10 & 17 & 24 y 31 y 38 & 45 & 52 & 59 y 66\\
   \ hline\ begin {array} {l}
   \ text {Mi peso}\\
   \ text {en libras}
   \ end {array} & 238.4 & 235.8 & 235.0 & 234.2 & 236.2 & 236.2 & 235.2 & 233.2 & 236.8 & 238.2\
   \ hline
   \ end {array}
   \ end {alineado}\)

   1. Encuentra la línea de mínimos cuadrados para los datos del jueves y comenta su bondad de ajuste.
   2. Encuentra la línea de mínimos cuadrados para los datos del sábado y comenta su bondad de ajuste.
   3. Utilice Regresión Cuadrática para encontrar una parábola que modele los datos del sábado y comente su bondad de ajuste.
   4. Comparar y contrastar las predicciones que hacen los tres modelos para mi peso el 1 de enero de 2010 (Día #366). ¿Se puede utilizar alguno de estos modelos para hacer una predicción de mi peso dentro de 20 años? Explica tu respuesta.
   5. ¿Por qué es esto una lección de honestidad cívica? Bueno, compara los dos modelos lineales que obtuviste anteriormente. Uno encajaba bien y el otro no, sin embargo ambos provenían de selecciones cuidadosas de datos reales. Al presentarte las tablas, no he mentido sobre mi peso, ni has usado malas matemáticas para falsificar las predicciones. La palabra que estamos buscando aquí es “desingenua”. Búscalo y luego discute las implicaciones que este tipo de manipulación de datos podría tener en un entorno más amplio, más complejo y motivado políticamente. (Incluso Obi-Wan le presentó la verdad a Luke solo “desde cierto punto de vista”).
6. (Datos que no son ni lineales ni cuadráticos.) Cerraremos este conjunto de ejercicios con dos conjuntos de datos que, por razones presentadas más adelante en el libro, no pueden modelarse correctamente por líneas o parábolas. Es un buen ejercicio, sin embargo, para ver qué sucede cuando se intenta utilizar un modelo lineal o cuadrático cuando no es apropiado.
   1. Este primer conjunto de datos provino de una publicación de verano de 2003 de la Liga de Protección Animal del Condado de Portage llamada “Tattle Tails”. Hacen la siguiente declaración y luego tienen un gráfico de datos que lo sustenta. “No tarda mucho en que dos gatos se conviertan en 80 millones. Si dos gatos y su descendencia sobreviviente se reprodujeran durante diez años, terminarías con 80,399,780 gatos”. Asumimos$N(0) = 2$.

      \ (\\ begin {array} {|l|c|c|r|r|r|r|r|r|r|r|r|}
      \ hline\ text {Año} x & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 &10\\ hline
      \ texto {Número de} & & & & & & & & & & & & & & & &\
      \ texto {Gatos} N (x) & 12 & 66 & 382 & 2201 & 12680 & 73041 & 420715 & 2423316 & 13968290 & 80399780\
      \ hline
      \ end {array}\)

      Utilice Regresión Cuadrática para encontrar una parábola que modele estos datos y comente su bondad de ajuste. (Alerta de spoiler: ¿Alguien sabe qué tipo de función necesitamos aquí?)

   2. Este siguiente conjunto de datos proviene del Observatorio Naval de Estados Unidos. Ese sitio tiene un montón de cosas increíbles, pero para este ejercicio utilicé los horarios de amanecer/atardecer en Fairbanks, Alaska para 2009 para darte un gráfico de la cantidad de horas de luz que reciben en cada mes.$21^{\mbox{st}}$ Dejaremos$x = 1$ representar el 21 de enero de 2009,$x = 2$ representar el 21 de febrero de 2009, y así sucesivamente.

      \ (\\ begin {array} {|l|r|r|r|r|r|r|r|r|r|r|r|r|r|}
      \ hline\ begin {array} {l}
      \ text {Mes}\
      \ texto {Número}
      \ end {array} & 1 y 2 y 3 y 4 y 5 y 6 y 7 y 8 y 9 y 10 y 11 y 12\\
      \ hline\ begin {array} {l}
      \ text {Horas de}\\
      \ text {Daylight}
      \ end {array} & 5.8 & 9.3 & 12.4 & 15.9 & 19.4 & 21.8 & 19.4 & 19.4 & 15.6 & 12.4 & 9.1 & 5.6 & 3.3\\
      \ hline
      \ end {array}\)

      Utilice Regresión Cuadrática para encontrar una parábola que modele estos datos y comente su bondad de ajuste. (Alerta de spoiler: ¿Alguien sabe qué tipo de función necesitamos aquí?)

2.5.2 Respuestas

1. 1. $y = 936.31x - 1645322.6$con$r=0.9696$ lo que indica un buen ajuste. La pendiente$936.31$ indica que la población del condado de Lake está aumentando a una tasa de (aproximadamente) 936 personas por año.
   2. Según el modelo, la población en 2010 será$236, \!660$.
   3. Según el modelo, la población del condado de Lake llegará en$250,\!000$ algún momento entre 2024 y 2025.
2. 1. $y = 796.8x - 1309762.5$con$r=0.8916$ lo que indica un ajuste razonable. La pendiente$796.8$ indica que la población del condado de Lorain está aumentando a una tasa de (aproximadamente) 797 personas por año.
   2. Según el modelo, la población en 2010 será$291, \! 805$.
   3. Según el modelo, la población de Lake County llegará en$325,\!000$ algún momento entre 2051 y 2052.
3. 3. $y = 0.266x - 459.86$con$r = 0.9607$ lo que indica un buen ajuste. La pendiente$0.266$ indica que la producción de energía del país está aumentando a una tasa de$0.266$ Quad por año.
   4. Según el modelo, la producción en 2010 será$74.8$ Quad.
   5. Según el modelo, la producción llegará a$100$ Quad en el año 2105.
4. La línea es$y = 36.8x + 16.39$. Tenemos$r = .99987$ y$r^{2} = .9997$ así este es un excelente ajuste a los datos. La pendiente$36.8$ representa millas por galón.
5. 1. La línea para los datos del jueves es$y = -.12x + 237.69$. Tenemos$r = -.9568$ y$r^{2} = .9155$ entonces este es un muy buen ajuste.
   2. La línea para los datos del sábado es$y = -0.000693x + 235.94$. Tenemos$r = -0.008986$ y$r^{2} = 0.0000807$ lo cual es horrible. Estos datos ni siquiera son cercanos a lineales.
   3. La parábola para los datos del sábado es$y = 0.003x^{2} - 0.21x + 238.30$. Tenemos$R^{2} = .47497$ lo que no es bueno. Por lo tanto, los datos tampoco son modelados bien por una función cuadrática.
   4. El modelo lineal del jueves tenía mi peso el 1 de enero de 2010 en 193.77 libras. Los modelos sabatinos dan 235.69 y 563.31 libras, respectivamente. La línea del jueves tiene mi peso por debajo de 0 libras en unos cinco años y medio, así que eso no sirve de nada. El cuadrático tiene un coeficiente de liderazgo positivo que significaría un aumento de peso sin límites para el resto de mi vida. La línea del sábado, que matemáticamente no se ajusta en absoluto a los datos, arroja una predicción de peso plausible al final. Creo que por eso los adultos hablan de “Mentiras, Malditas mentiras y estadísticas”.
6. 1. El modelo cuadrático para los gatos en el condado de Portage es$y = 1917803.54x^{2} - 16036408.29x + 24094857.7$. Aunque$R^{2} = .70888$ este no es un buen modelo porque está muy lejos para valores pequeños de$x$. Caso en punto, el modelo nos da 24,094,858 gatos cuando$x = 0$ pero sabemos$N(0) = 2$.
   2. El modelo cuadrático para las horas de luz en Fairbanks, Alaska es$y = .51x^{2} + 6.23x - .36$. Incluso con$R^{2} = .92295$ nosotros debemos tener cuidado de hacer predicciones más allá de los datos. Caso en punto, el modelo da$-4.84$ horas de luz cuando$x = 13$. ¿Entonces el 21 de enero de 2010 será “extra oscuro”? Obviamente una parábola apuntando hacia abajo no nos está contando toda la historia.

Referencia

¹ y autores con más experiencia en esta área,

² Como Cálculo y Álgebra Lineal

³ Remitimos al lector interesado a un curso de Estadística para explorar la significación de$\ r$ y$\ r^{2}$.

⁴ Ver esta actividad del Departamento de Energía

⁵ La unidad 1 Quad es 1 Cuadrillion =$\ 10^{15}$ BTU, que es suficiente calor para elevar el lago Erie aproximadamente$\ 1^{\circ} \mathrm{F}$

⁶ http://www.ohiobiz.com/census/Lake.pdf

⁷ Desarrollaremos modelos más sofisticados para el crecimiento de las poblaciones en el Capítulo 6. Por el momento, utilizamos un teorema de Cálculo para aproximar esas funciones con líneas.

⁸ http://www.ohiobiz.com/census/Lorain.pdf