4.10: Antiderivados
- Page ID
- 116472
- Encuentra la antiderivada general de una función dada.
- Explicar los términos y notación utilizados para una integral indefinida.
- Declarar la regla de poder para integrales.
- Utilizar la antidiferenciación para resolver problemas simples de valor inicial.
En este punto, hemos visto cómo calcular derivadas de muchas funciones y se han introducido en una variedad de sus aplicaciones. Ahora hacemos una pregunta que da la vuelta a este proceso: Dada una función\(f\), ¿cómo encontramos una función con la derivada\(f\) y por qué nos interesaría esa función?
Respondemos a la primera parte de esta pregunta definiendo antiderivados. La antiderivada de una función\(f\) es una función con una derivada\(f\). ¿Por qué nos interesan los antiderivados? La necesidad de antiderivados surge en muchas situaciones, y observamos diversos ejemplos a lo largo del resto del texto. Aquí examinamos un ejemplo específico que involucra el movimiento rectilíneo. En nuestro examen en Derivadas del movimiento rectilíneo, demostramos que dada una función\(s(t)\) de posición de un objeto, entonces su función de velocidad\(v(t)\) es la derivada de\(s(t)\) —es decir,\(v(t)=s′(t)\). Además, la aceleración\(a(t)\) es la derivada de la velocidad\(v(t)\), es decir,\(a(t)=v′(t)=s''(t)\). Ahora supongamos que se nos da una función de aceleración\(a\), pero no la función de velocidad\(v\) o la función de posición\(s\). Ya que\(a(t)=v′(t)\), determinar la función de velocidad nos obliga a encontrar una antiderivada de la función de aceleración. Entonces, ya que la\(v(t)=s′(t),\) determinación de la función de posición nos obliga a encontrar una antiderivada de la función de velocidad. El movimiento rectilíneo es solo un caso en el que surge la necesidad de antiderivados. Veremos muchos más ejemplos a lo largo del resto del texto. Por ahora, veamos la terminología y notación para los antiderivados, y determinemos los antiderivados para varios tipos de funciones. Examinamos diversas técnicas para encontrar antiderivados de funciones más complicadas posteriormente en el texto (Introducción a las Técnicas de Integración).
El reverso de la diferenciación
En este punto, sabemos encontrar derivadas de diversas funciones. Ahora hacemos la pregunta opuesta. Dada una función\(f\), ¿cómo podemos encontrar una función con derivada\(f\)? Si podemos encontrar una función\(F\) con derivada\(f,\) llamamos\(F\) antiderivada de\(f\).
Una función\(F\) es una antiderivada de la función\(f\) si
\[F′(x)=f(x) \nonumber \]
para todos\(x\) en el dominio de\(f\).
Considera la función\(f(x)=2x\). Conociendo la regla de poder de diferenciación, concluimos que\(F(x)=x^2\) es un antiderivado del\(f\) ya\(F′(x)=2x\).
¿Existen otros antiderivados de\(f\)?
Sí; ya que la derivada de cualquier constante\(C\) es cero, también\(x^2+C\) es una antiderivada de\(2x\). Por lo tanto,\(x^2+5\) y también\(x^2−\sqrt{2}\) son antiderivados.
¿Hay otros que no sean de la forma\(x^2+C\) para alguna constante\(C\)?
La respuesta es no. A partir del Corolario 2 del Teorema del Valor Medio, sabemos que si\(F\) y\(G\) son funciones diferenciables tales que\(F′(x)=G′(x),\) entonces\(F(x)−G(x)=C\) para alguna constante\(C\). Este hecho lleva al siguiente teorema importante.
Dejar\(F\) ser una antiderivada de\(f\) más de un intervalo\(I\). Entonces,
- para cada constante\(C\), la función\(F(x)+C\) es también una antiderivada de\(f\) más\(I\);
- si\(G\) es un antiderivado de\(f\) más\(I\), hay una constante\(C\) para la cual\(G(x)=F(x)+C\) sobre\(I\).
En otras palabras, la forma más general de la antiderivada de\(f\) over\(I\) es\(F(x)+C\).
Utilizamos este hecho y nuestro conocimiento de derivados para encontrar todos los antiderivados para varias funciones.
Para cada una de las siguientes funciones, encuentra todos los antiderivados.
- \(f(x)=3x^2\)
- \(f(x)=\dfrac{1}{x}\)
- \(f(x)=\cos x\)
- \(f(x)=e^x\)
Solución:
a. Porque
\[\dfrac{d}{dx}\left(x^3\right)=3x^2 \nonumber \]
entonces\(F(x)=x^3\) es un antiderivado de\(3x^2\). Por lo tanto, cada antiderivado de\(3x^2\) es de la forma\(x^3+C\) para alguna constante\(C\), y cada función de la forma\(x^3+C\) es un antiderivado de\(3x^2\).
b. dejar\(f(x)=\ln |x|.\)
Para\(x>0,\; f(x)=\ln |x|=\ln (x)\) y
\[\dfrac{d}{dx}\Big(\ln x\Big)=\dfrac{1}{x}. \nonumber \]
Para\(x<0,\; f(x)=\ln |x|=\ln (−x)\) y
\[\dfrac{d}{dx}\Big(\ln (−x)\Big)=−\dfrac{1}{−x}=\dfrac{1}{x}. \nonumber \]
Por lo tanto,
\[\dfrac{d}{dx}\Big(\ln |x|\Big)=\dfrac{1}{x}. \nonumber \]
Así,\(F(x)=\ln |x|\) es un antiderivado de\(\dfrac{1}{x}\). Por lo tanto, cada antiderivado de\(\dfrac{1}{x}\) es de la forma\(\ln |x|+C\) para alguna constante\(C\) y cada función de la forma\(\ln |x|+C\) es un antiderivado de\(\dfrac{1}{x}\).
c. Tenemos
\[\dfrac{d}{dx}\Big(\sin x\Big)=\cos x, \nonumber \]
así\(F(x)=\sin x\) es un antiderivado de\(\cos x\). Por lo tanto, cada antiderivado de\(\cos x\) es de la forma\(\sin x+C\) para alguna constante\(C\) y cada función de la forma\(\sin x+C\) es un antiderivado de\(\cos x\).
d. desde
\[\dfrac{d}{dx}\left(e^x\right)=e^x, \nonumber \]
entonces\(F(x)=e^x\) es un antiderivado de\(e^x\). Por lo tanto, cada antiderivado de\(e^x\) es de la forma\(e^x+C\) para alguna constante\(C\) y cada función de la forma\(e^x+C\) es un antiderivado de\(e^x\).
Encuentra todos los antiderivados de\(f(x)=\sin x\).
- Pista
-
¿De qué función tiene un derivado\(\sin x\)?
- Contestar
-
\(F(x) = −\cos x+C\)
Integrales indefinidas
Ahora analizamos la notación formal utilizada para representar antiderivados y examinar algunas de sus propiedades. Estas propiedades nos permiten encontrar antiderivados de funciones más complicadas. Dada una función\(f\), usamos la notación\(f′(x)\) o\(\dfrac{df}{dx}\) para denotar la derivada de\(f\). Aquí introducimos notación para antiderivados. Si\(F\) es un antiderivado de\(f\), decimos que\(F(x)+C\) es el antiderivado más general de\(f\) y escribimos
\[\int f(x)\,dx=F(x)+C.\nonumber \]
El símbolo\(\displaystyle \int \) se llama un signo integral, y\(\displaystyle \int f(x)\,dx\) se llama la integral indefinida de\(f\).
Dada una función\(f\), la integral indefinida de\(f\), denotada
\[\int f(x)\,dx, \nonumber \]
es el antiderivado más general de\(f\). Si\(F\) es un antiderivado de\(f\), entonces
\[\int f(x)\,dx=F(x)+C. \nonumber \]
La expresión\(f(x)\) se llama integrando y la variable\(x\) es la variable de integración.
Dada la terminología introducida en esta definición, el acto de encontrar los antiderivados de una función\(f\) suele denominarse integrador\(f\).
Para una función\(f\) y una antiderivada\(F\), las funciones\(F(x)+C\), donde\(C\) está cualquier número real, a menudo se conoce como la familia de antiderivados de\(f\). Por ejemplo, ya que\(x^2\) es un antiderivado de\(2x\) y cualquier antiderivado de\(2x\) es de la forma\(x^2+C,\) que escribimos
\[\int 2x\,dx=x^2+C.\nonumber \]
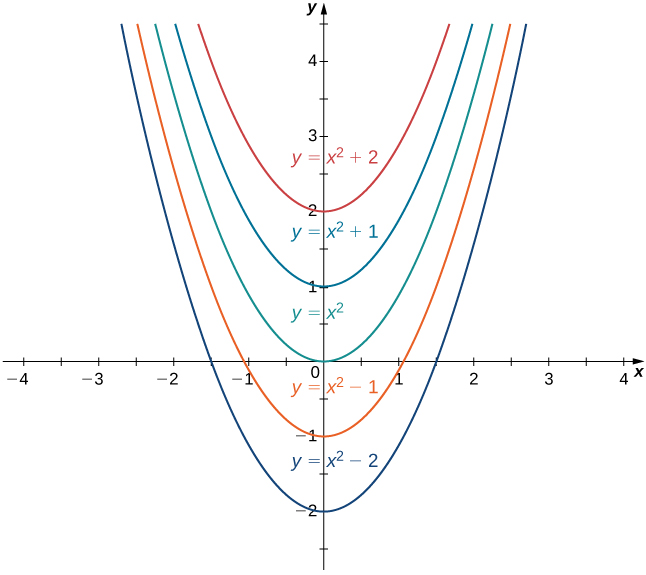
El acervo de todas las funciones de la forma\(x^2+C,\) donde\(C\) se encuentra cualquier número real, se conoce como la familia de antiderivados de\(2x\). La figura\(\PageIndex{1}\) muestra una gráfica de esta familia de antiderivados.
Para algunas funciones, la evaluación de integrales indefinidas se deriva directamente de las propiedades de los derivados. Por ejemplo, para\(n≠−1\),
\(\displaystyle \int x^n\,dx=\dfrac{x^{n+1}}{n+1}+C,\)
que proviene directamente de
\(\dfrac{d}{dx}\left(\dfrac{x^{n+1}}{n+1}\right)=(n+1)\dfrac{x^n}{n+1}=x^n\).
Este hecho se conoce como la regla de poder para integrales.
Para\(n≠−1,\)
\[\int x^n\,dx=\dfrac{x^{n+1}}{n+1}+C. \nonumber \]
Evaluar integrales indefinidas para algunas otras funciones también es un cálculo sencillo. En la siguiente tabla se enumeran las integrales indefinidas para varias funciones comunes. Una lista más completa aparece en el Apéndice B.
| Fórmula de diferenciación | Integral indefinida |
|---|---|
| \(\dfrac{d}{dx}\Big(k\Big)=0\) | \(\displaystyle \int k\,dx=\int kx^0\,dx=kx+C\) |
| \(\dfrac{d}{dx}\Big(x^n\Big)=nx^{n−1}\) | \(\displaystyle \int x^n\,dx=\dfrac{x^{n+1}}{n+1}+C\)para\(n≠−1\) |
| \(\dfrac{d}{dx}\Big(\ln |x|\Big)=\dfrac{1}{x}\) | \(\displaystyle \int \dfrac{1}{x}\,dx=\ln |x|+C\) |
| \(\dfrac{d}{dx}\Big(e^x\Big)=e^x\) | \(\displaystyle \int e^x\,dx=e^x+C\) |
| \(\dfrac{d}{dx}\Big(\sin x\Big)=\cos x\) | \(\displaystyle \int \cos x\,dx=\sin x+C\) |
| \(\dfrac{d}{dx}\Big(\cos x\Big)=−\sin x\) | \(\displaystyle \int \sin x\,dx=−\cos x+C\) |
| \(\dfrac{d}{dx}\Big(\tan x\Big)=\sec^2 x\) | \(\displaystyle \int \sec^2 x\,dx=\tan x+C\) |
| \(\dfrac{d}{dx}\Big(\csc x\Big)=−\csc x\cot x\) | \(\displaystyle \int \csc x\cot x\,dx=−\csc x+C\) |
| \(\dfrac{d}{dx}\Big(\sec x\Big)=\sec x\tan x\) | \(\displaystyle \int \sec x\tan x\,dx=\sec x+C\) |
| \(\dfrac{d}{dx}\Big(\cot x\Big)=−\csc^2 x\) | \(\displaystyle \int \csc^2x\,dx=−\cot x+C\) |
| \(\dfrac{d}{dx}\Big(\sin^{−1}x\Big)=\dfrac{1}{\sqrt{1−x^2}}\) | \(\displaystyle \int \dfrac{1}{\sqrt{1−x^2}}=\sin^{−1}x+C\) |
| \(\dfrac{d}{dx}\Big(\tan^{−1}x\Big)=\dfrac{1}{1+x^2}\) | \(\displaystyle \int \dfrac{1}{1+x^2}\,dx=\tan^{−1}x+C\) |
| \(\dfrac{d}{dx}\Big(\sec^{−1}|x|\Big)=\dfrac{1}{x\sqrt{x^2−1}}\) | \(\displaystyle \int \dfrac{1}{x\sqrt{x^2−1}}\,dx=\sec^{−1}|x|+C\) |
De la definición de integral indefinida de\(f\), sabemos
\[\int f(x)\,dx=F(x)+C\nonumber \]
si y sólo si\(F\) es un antiderivado de\(f\).
Por lo tanto, al afirmar que
\[\int f(x)\,dx=F(x)+C\nonumber \]
es importante verificar si esta afirmación es correcta verificando que\(F′(x)=f(x).\)
Cada una de las siguientes declaraciones es de la forma\(\displaystyle \int f(x)\,dx=F(x)+C.\) Verificar que cada declaración sea correcta mostrando que\(F′(x)=f(x).\)
- \(\displaystyle\int \big(x+e^x\big)\,dx=\dfrac{x^2}{2}+e^x+C\)
- \(\displaystyle\int xe^x\,dx=xe^x−e^x+C\)
Solución:
a. desde
\(\dfrac{d}{dx}\left(\dfrac{x^2}{2}+e^x+C\right)=x+e^x\),
la declaración
\[\int \big(x+e^x\big)\,dx=\dfrac{x^2}{2}+e^x+C \nonumber \]
es correcto.
Tenga en cuenta que estamos verificando una integral indefinida para una suma. Además,\(\dfrac{x^2}{2}\) y\(e^x\) son antiderivados de\(x\) y\(e^x\), respectivamente, y la suma de los antiderivados es una antiderivada de la suma. Volvemos a discutir este hecho más adelante en esta sección.
b. Usando la regla del producto, vemos que
\[\dfrac{d}{dx}\left(xe^x−e^x+C\right)=e^x+xe^x−e^x=xe^x. \nonumber \]
Por lo tanto, la declaración
\[\int xe^x\,dx=xe^x−e^x+C \nonumber \]
es correcto.
Tenga en cuenta que estamos verificando una integral indefinida para un producto. El antiderivado no\(xe^x−e^x\) es un producto de los antiderivados. Además, el producto de los antiderivados, no\(x^2e^x/2\) es un antiderivado de\(xe^x\) desde
\(\dfrac{d}{dx}\left(\dfrac{x^2e^x}{2}\right)=xe^x+\dfrac{x^2e^x}{2}≠xe^x\).
En general, el producto de antiderivados no es un antiderivado de un producto.
Verificar que\(\displaystyle \int x\cos x\,\,dx=x\sin x+\cos x+C.\)
- Pista
-
Calcular\(\dfrac{d}{dx}\Big(x\sin x+\cos x+C\Big).\)
- Contestar
-
\(\dfrac{d}{dx}\Big(x\sin x+\cos x+C\Big)=\sin x+x\cos x−\sin x=x \cos x\)
En Table\(\PageIndex{1}\), enumeramos las integrales indefinidas para muchas funciones elementales. Ahora volvamos nuestra atención a evaluar integrales indefinidas para funciones más complicadas. Por ejemplo, considere encontrar una antiderivada de una suma\(f+g\). En Ejemplo\(\PageIndex{2}a\) mostramos que una antiderivada de la suma\(x+e^x\) viene dada por la suma\(\dfrac{x^2}{2}+e^x\) —es decir, una antiderivada de una suma viene dada por una suma de antiderivados. Este resultado no fue específico de este ejemplo. En general, si\(F\) y\(G\) son antiderivadas de cualquier función\(f\) y\(g\), respectivamente, entonces
\(\dfrac{d}{dx}\big(F(x)+G(x)\big)=F′(x)+G′(x)=f(x)+g(x).\)
Por lo tanto,\(F(x)+G(x)\) es un antiderivado de\(f(x)+g(x)\) y tenemos
\[ \int \big(f(x)+g(x)\big)\,dx=F(x)+G(x)+C.\nonumber \]
Del mismo modo,
\[ \int \big(f(x)−g(x)\big)\,dx=F(x)−G(x)+C.\nonumber \]
Además, considere la tarea de encontrar un antiderivado de\(kf(x),\) dónde\(k\) está cualquier número real. Desde
\[ \dfrac{d}{dx}\Big(kF(x)\Big)=k\dfrac{d}{dx}\Big(F(x)\Big)=kF′(x)\nonumber \]
para cualquier número real\(k\), concluimos que
\[ \int kf(x)\,dx=kF(x)+C.\nonumber \]
Estas propiedades se resumen a continuación.
Dejar\(F\) y\(G\) ser antiderivados de\(f\) y\(g\), respectivamente, y dejar\(k\) ser cualquier número real.
Sumas y diferencias
\[\int \big(f(x)±g(x)\big)\,dx=F(x)±G(x)+C \nonumber \]
Multiplos Constantes
\[ \int kf(x)\,dx=kF(x)+C \nonumber \]
A partir de este teorema, podemos evaluar cualquier integral que involucre una suma, diferencia o múltiplo constante de funciones con antiderivadas que se conocen. Evaluar integrales que involucran productos, cocientes o composiciones es más complicado. (Ver Ejemplo\(\PageIndex{2}b\) para un ejemplo que involucra un antiderivado de un producto.) Observamos y abordamos integrales que involucran estas funciones más complicadas en Introducción a la Integración. En el siguiente ejemplo, examinamos cómo utilizar este teorema para calcular las integrales indefinidas de varias funciones.
Evaluar cada una de las siguientes integrales indefinidas:
- \(\displaystyle \int \big(5x^3−7x^2+3x+4\big)\,dx\)
- \(\displaystyle \int \dfrac{x^2+4\sqrt[3]{x}}{x}\,dx\)
- \(\displaystyle \int \dfrac{4}{1+x^2}\,dx\)
- \(\displaystyle \int \tan x\cos x\,dx\)
Solución:
a. Usando Propiedades de Integrales Indefinidas, podemos integrar cada uno de los cuatro términos en el integrando por separado. Obtenemos
\(\displaystyle \int \big(5x^3−7x^2+3x+4\big)\,dx=\int 5x^3\,dx−\int 7x^2\,dx+\int 3x\,dx+\int 4\,dx.\)
A partir de la segunda parte de Propiedades de Integrales Indefinidas, cada coeficiente puede escribirse frente al signo integral, lo que da
\(\displaystyle \int 5x^3\,dx−\int 7x^2\,dx+\int 3x\,dx+\int 4\,dx=5\int x^3\,dx−7\int x^2\,dx+3\int x\,dx+4\int 1\,dx.\)
Usando la regla de potencia para integrales, concluimos que
\(\displaystyle \int \big(5x^3−7x^2+3x+4\big)\,dx=\dfrac{5}{4}x^4−\dfrac{7}{3}x^3+\dfrac{3}{2}x^2+4x+C.\)
b. Reescribir el integrando como
\(\dfrac{x^2+4\sqrt[3]{x}}{x}=\dfrac{x^2}{x}+\dfrac{4\sqrt[3]{x}}{x}.\)
Entonces, para evaluar la integral, integrar cada uno de estos términos por separado. Usando la regla de poder, tenemos
\ [\ begin {align*}\ int\ izquierda (x+\ dfrac {4} {x^ {2/3}}\ derecha)\, dx&=\ int x\, dx+4\ int x^ {−2/3}\, dx\\ [4pt]
&=\ dfrac {1} {2} x^2+4\ dfrac {1} {\ izquierda (\ tfrac {−2} {3}\ derecha) +1} x^ {(−2/3) +1} +C\\ [4pt]
&=\ dfrac {1} {2} x^2+12x^ {1/3} +C.\ end {align*}\]
c. Usando Propiedades de Integrales Indefinidas, escribe la integral como
\(4\displaystyle \int \dfrac{1}{1+x^2}\,dx.\)
Entonces, use el hecho de que\(\tan^{−1}(x)\) es un antiderivado de\(\dfrac{1}{1+x^2}\) para concluir que
\(\displaystyle \int \dfrac{4}{1+x^2}\,dx=4\tan^{−1}(x)+C.\)
d. Reescribir el integrando como
\(\tan x\cos x=\dfrac{\sin x}{\cos x}\cdot\cos x=\sin x.\)
Por lo tanto,
\(\displaystyle \int \tan x\cos x\,dx=\int \sin x\,dx=−\cos x+C.\)
Evaluar\(\displaystyle \int \big(4x^3−5x^2+x−7\big)\,dx\).
- Pista
-
Integrar cada término en el integrando por separado, haciendo uso de la regla de poder.
- Responder
-
\(\displaystyle \int \big(4x^3−5x^2+x−7\big)\,dx = \quad x^4−\dfrac{5}{3}x^3+\dfrac{1}{2}x^2−7x+C\)
Problemas de valor inicial
Analizamos técnicas para integrar una gran variedad de funciones que involucran productos, cocientes y composiciones más adelante en el texto. Aquí pasamos a un uso común para los antiderivados que surge a menudo en muchas aplicaciones: resolver ecuaciones diferenciales.
Una ecuación diferencial es una ecuación que relaciona una función desconocida y una o más de sus derivadas. La ecuación
es un ejemplo sencillo de una ecuación diferencial. Resolver esta ecuación significa encontrar una función\(y\) con una derivada\(f\). Por lo tanto, las soluciones de la Ecuación\ ref {diffeq1} son los antiderivados de\(f\). Si\(F\) es una antiderivada de\( f\), cada función de la forma\( y=F(x)+C\) es una solución de esa ecuación diferencial. Por ejemplo, las soluciones de
están dadas por
A veces nos interesa determinar si una determinada curva de solución pasa por cierto punto\( (x_0,y_0)\), es decir,\( y(x_0)=y_0\). El problema de encontrar una función\(y\) que satisfaga una ecuación diferencial
con la condición adicional
es un ejemplo de un problema de valor inicial. El padecimiento\( y(x_0)=y_0\) se conoce como condición inicial. Por ejemplo, buscar una función\( y\) que satisfaga la ecuación diferencial
y la condición inicial
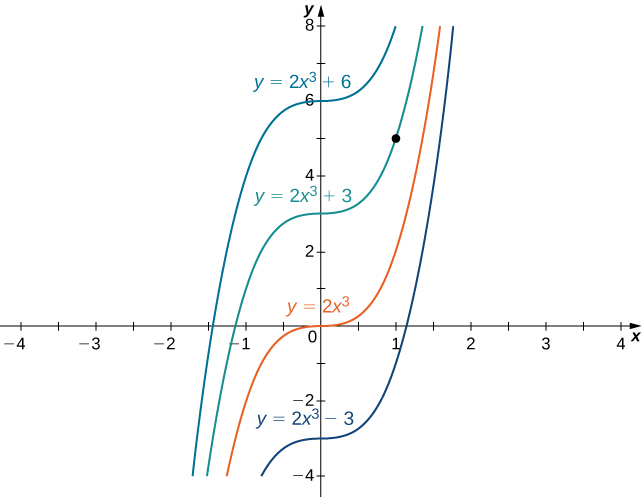
es un ejemplo de un problema de valor inicial. Dado que las soluciones de la ecuación diferencial son\( y=2x^3+C,\) encontrar una función\(y\) que también satisfaga la condición inicial, necesitamos encontrar\(C\) tal que\(y(1)=2(1)^3+C=5\). A partir de esta ecuación, vemos eso\( C=3\), y concluimos que\( y=2x^3+3\) es la solución de este problema de valor inicial como se muestra en la siguiente gráfica.
Resolver el problema del valor inicial
\[\dfrac{dy}{dx}=\sin x,\quad y(0)=5.\nonumber \]
Solución
Primero tenemos que resolver la ecuación diferencial. Si\(\dfrac{dy}{dx}=\sin x\), entonces
\[y=\displaystyle \int \sin(x)\,dx=−\cos x+C.\nonumber \]
A continuación tenemos que buscar una solución\(y\) que satisfaga la condición inicial. La condición inicial\(y(0)=5\) significa que necesitamos una constante\(C\) tal que\(−\cos x+C=5.\) Por lo tanto,
\[C=5+\cos(0)=6.\nonumber \]
La solución del problema del valor inicial es\(y=−\cos x+6.\)
Resolver el problema de valor inicial\(\dfrac{dy}{dx}=3x^{−2},\quad y(1)=2\).
- Pista
-
Encuentra todos los antiderivados de\(f(x)=3x^{−2.}\)
- Responder
-
\(y=−\dfrac{3}{x}+5\)
Los problemas de valor inicial surgen en muchas aplicaciones. A continuación consideramos un problema en el que un conductor aplica los frenos en un automóvil. Nos interesa el tiempo que tarda el auto en detenerse. Recordemos que la función de velocidad\(v(t)\) es la derivada de una función de posición\(s(t),\) y la aceleración\(a(t)\) es la derivada de la función de velocidad. En ejemplos anteriores en el texto, podríamos calcular la velocidad desde la posición y luego calcular la aceleración a partir de la velocidad. En el siguiente ejemplo trabajamos al revés. Dada una función de aceleración, calculamos la función de velocidad. Luego usamos la función de velocidad para determinar la función de posición.
Un automóvil viaja a la velocidad de\(88\) pies/seg (\(60\)mph) cuando se aplican los frenos. El automóvil comienza a desacelerar a una velocidad constante de\(15\) pies/seg 2.
- ¿Cuántos segundos transcurren antes de que el auto se detenga?
- ¿A qué distancia recorre el auto durante ese tiempo?
Solución
a. Primero introducimos variables para este problema. Deje\(t\) ser el tiempo (en segundos) después de que se apliquen los frenos por primera vez. Dejar\(a(t)\) ser la aceleración del carro (en pies por segundos cuadrados) en el momento\(t\). Dejar\(v(t)\) ser la velocidad del carro (en pies por segundo) a la vez\(t\). Deja\(s(t)\) ser la posición del auto (en pies) más allá del punto donde se aplican los frenos en el momento\(t\).
El automóvil viaja a una velocidad de\(88\) ft/seg. Por lo tanto, la velocidad inicial es\(v(0)=88\) ft/seg. Dado que el auto está desacelerando, la aceleración es
\(a(t)=−15\,\text{ft/sec}^2\).
La aceleración es la derivada de la velocidad,
\(v′(t)=-15.\)
Por lo tanto, tenemos un problema de valor inicial que resolver:
\(v′(t)=−15,\quad v(0)=88.\)
Integrando, encontramos que
\(v(t)=−15t+C.\)
Desde\(v(0)=88,C=88.\) Así, la función de velocidad es
\(v(t)=−15t+88.\)
Para saber cuánto tiempo tarda el auto en detenerse, necesitamos encontrar el tiempo\(t\) tal que la velocidad sea cero. Resolviendo\(−15t+88=0,\) obtenemos\(t=\dfrac{88}{15}\) sec.
b. Para saber qué tan lejos viaja el automóvil durante este tiempo, necesitamos encontrar la posición del automóvil después del\(\dfrac{88}{15}\) sec. Sabemos que la velocidad\(v(t)\) es la derivada de la posición\(s(t)\). Considera que la posición inicial es\(s(0)=0\). Por lo tanto, necesitamos resolver el problema del valor inicial
\(s′(t)=−15t+88,\quad s(0)=0.\)
Integrando, tenemos
\(s(t)=−\dfrac{15}{2}t^2+88t+C.\)
Ya que\(s(0)=0\), la constante es\(C=0\). Por lo tanto, la función de posición es
\(s(t)=−\dfrac{15}{2}t^2+88t.\)
Después de\(t=\frac{88}{15}\) sec, la posición es\(s\left(\frac{88}{15}\right)≈258.133\) ft.
Supongamos que el auto viaja a razón de\(44\) ft/seg. ¿Cuánto tiempo tarda en detenerse el auto? ¿Hasta dónde viajará el auto?
- Pista
-
\(v(t)=−15t+44.\)
- Responder
-
\(2.93\)seg,\(64.5\) ft
Conceptos clave
- Si\(F\) es un antiderivado de\(f,\) entonces cada antiderivado de\(f\) es de la forma\(F(x)+C\) para alguna constante\(C\).
- Resolver el problema del valor inicial\[\dfrac{dy}{dx}=f(x),\quad y(x_0)=y_0 \nonumber \] requiere primero encontrar el conjunto de antiderivados de\(f\) y luego buscar el antiderivado particular que también satisfaga la condición inicial.
Glosario
- antiderivado
- una función\(F\) tal que\(F′(x)=f(x)\) para todos\(x\) en el dominio de\(f\) es un antiderivado de\(f\)
- integral indefinida
- la antiderivada más general de\(f(x)\) es la integral indefinida de\(f\); utilizamos la notación\(\displaystyle \int f(x)\,dx\) para denotar la integral indefinida de\(f\)
- problema de valor inicial
- un problema que requiere encontrar una función\(y\) que satisfaga la ecuación diferencial\(\dfrac{dy}{dx}=f(x)\) junto con la condición inicial\(y(x_0)=y_0\)