9.5: Serie alterna

Objetivos de aprendizaje

• Utilice la prueba de serie alterna para probar una serie alterna para la convergencia.
• Estimar la suma de una serie alternada.
• Explicar el significado de convergencia absoluta y convergencia condicional.

En lo que va de este capítulo, hemos discutido principalmente series con términos positivos. En esta sección presentamos series alternas, aquellas series cuyos términos se alternan en signo. Mostraremos en un capítulo posterior que estas series suelen surgir al estudiar series de poder. Después de definir series alternas, introducimos la prueba de series alternas para determinar si dicha serie converge.

La prueba de la serie alterna

Una serie cuyos términos alternan entre valores positivos y negativos es una serie alterna. Por ejemplo, la serie

\[\sum_{n=1}^∞ \left(−\dfrac{1}{2} \right)^n=−\dfrac{1}{2}+\dfrac{1}{4}−\dfrac{1}{8}+\dfrac{1}{16}− \ldots \label{eq1} \]

y

\[\sum_{n=1}^∞\dfrac{(−1)^{n+1}}{n}=1−\dfrac{1}{2}+\dfrac{1}{3}−\dfrac{1}{4}+\ldots \label{eq2} \]

son ambas series alternas.

Definición: Serie alterna

Cualquier serie cuyos términos alternen entre valores positivos y negativos se denomina serie alterna. Una serie alterna se puede escribir en la forma

\[\sum_{n=1}^∞(−1)^{n+1}b_n=b_1−b_2+b_3−b_4+ \ldots \label{eq3} \]

o

\[\sum_{n−1}^∞(−1)^nb_n=−b_1+b_2−b_3+b_4−\ldots \label{eq4} \]

Donde\( b_n≥0\) para todos los enteros positivos\(n\).

La serie (1), mostrada en la Ecuación\ ref {eq1}, es una serie geométrica. Dado que\( |r|=|−1/2|<1,\) la serie converge. La serie (2), que se muestra en la Ecuación\ ref {eq2}, se denomina serie armónica alterna. Mostraremos que mientras la serie armónica diverge, la serie armónica alterna converge. Para probarlo, observamos la secuencia de sumas parciales\( \{S_k\}\) (Figura 1).

Prueba

Considera los términos impares\( S_{2k+1}\) para\( k≥0\). Desde\( 1/(2k+1)<1/2k,\)

\[S_{2k+1}=S_{2k−1}−\dfrac{1}{2k}+\dfrac{1}{2k+1}<S_{2k−1}. \nonumber \]

Por lo tanto,\( \{S_{2k+1}\}\) es una secuencia decreciente. También,

\[S_{2k+1}=\left(1−\dfrac{1}{2}\right)+\left(\dfrac{1}{3}−\dfrac{1}{4}\right)+ \ldots + \left(\dfrac{1}{2k−1}−\dfrac{1}{2k}\right)+\dfrac{1}{2k+1}>0. \nonumber \]

Por lo tanto,\( \{S_{2k+1}\}\) se limita a continuación. Ya que\( \{S_{2k+1}\}\) es una secuencia decreciente que está delimitada a continuación, por el Teorema de Convergencia Monótona,\( \{S_{2k+1}\}\) converge. Del mismo modo, los términos pares\( \{S_{2k}\}\) forman una secuencia creciente que está delimitada arriba porque

\[S_{2k}=S_{2k−2}+\dfrac{1}{2k−1}−\dfrac{1}{2k}>S_{2k−2} \nonumber \]

y

\[S_{2k}=1+ \left(−\dfrac{1}{2}+\dfrac{1}{3}\right)+\ldots + \left(−\dfrac{1}{2k−2}+\dfrac{1}{2k−1}\right)−\dfrac{1}{2k}<1. \nonumber \]

Por lo tanto, por el Teorema de Convergencia Monótona, la secuencia\( \{S_{2k}\}\) también converge. Desde

\[S_{2k+1}=S_{2k}+\dfrac{1}{2k+1}, \nonumber \]

sabemos que

\[\lim_{k→∞}S_{2k+1}=\lim_{k→∞}S_{2k}+\lim_{k→∞}\dfrac{1}{2k+1}. \nonumber \]

Dejar\(\displaystyle S=\lim_{k→∞}S_{2k+1}\) y usar el hecho de que\( 1/(2k+1)→0,\) concluimos eso\(\displaystyle \lim_{k→∞}S_{2k}=S\). Dado que los términos impares y los términos pares en la secuencia de sumas parciales convergen al mismo límite\( S\), se puede demostrar que la secuencia de sumas parciales converge a\( S\), y por lo tanto la serie armónica alterna converge a\( S\).

También se puede demostrar que\( S=\ln 2,\) y podemos escribir

\[\sum_{n=1}^∞\dfrac{(−1)^{n+1}}{n}=1−\dfrac{1}{2}+\dfrac{1}{3}−\dfrac{1}{4}+a\ldots=\ln (2). \nonumber \]

Figura\(\PageIndex{1}\): Para las series armónicas alternas, los términos impares\( S_{2k+1}\) en la secuencia de sumas parciales son decrecientes y acotados a continuación. Los términos parejos\( S_{2k}\) van en aumento y acotados por encima.

□

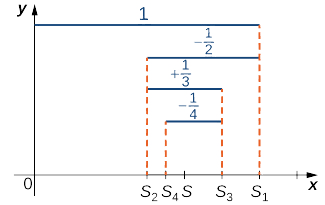
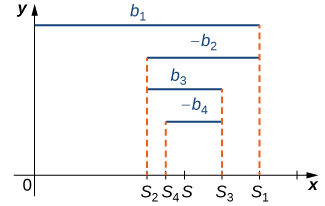
De manera más general, cualquier serie alterna de forma (3) (Ecuación\ ref {eq3}) o (4) (Ecuación\ ref {eq4}) converge siempre\( b_1≥b_2≥b_3≥⋯\) y cuando y\( b_n→0\) (Figura 2). La prueba es similar a la prueba para la serie armónica alterna.

Figura\(\PageIndex{2}\): Para una serie alterna\( b_1−b_2+b_3−⋯\) en la que\( b_1>b_2>b_3>⋯\), los términos impares\( S_{2k+1}\) en la secuencia de sumas parciales son decrecientes y acotados a continuación. Los términos parejos\( S_{2k}\) van en aumento y acotados por encima.

Prueba en serie alterna

Una serie alternante de la forma

\[\sum_{n=1}^∞(−1)^{n+1}b_n \nonumber \]o\[\sum_{n=1}^∞(−1)^nb_n \nonumber \]

converge si

1. \( 0≤b_{n+1}≤b_n\)para todos\( n≥1\) y
2. \(\displaystyle \lim_{n→∞}b_n=0.\)

Esto se conoce como la prueba en serie alterna.

Observamos que este teorema es cierto más generalmente siempre y cuando exista algún entero\( N\) tal que\( 0≤b_{n+1}≤b_n\) para todos\( n≥N.\)

Ejemplo\( \PageIndex{1}\): Convergence of Alternating Series

Para cada una de las siguientes series alternas, determine si la serie converge o diverge.

1. \(\displaystyle \sum^∞_{n=1}\frac{(−1)^{n+1}}{n^2}\)
2. \(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{n}{n+1}\)

Solución

a. desde\( \dfrac{1}{(n+1)^2}<\dfrac{1}{n^2}\) y\( \dfrac{1}{n^2}→0,\) la serie converge.

b. ya que\( n/(n+1)↛0\) as\( n→∞\), no podemos aplicar la prueba de series alternas. En su lugar, usamos la prueba de término n para la divergencia. Dado que\(\displaystyle \lim_{n→∞}\dfrac{n}{n+1}=1≠0,\) la serie diverge.

Ejercicio\(\PageIndex{1}\)

Determinar si la serie\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{n}{2^n}\) converge o diverge.

Pista

¿Está\( \left\{\frac{n}{2^n}\right\}\) disminuyendo? ¿Qué es\(\displaystyle \lim_{n→∞}\frac{n}{2^n}\)?

Contestar

La serie converge.

Resto de una serie alterna

Es difícil calcular explícitamente la suma de la mayoría de las series alternas, por lo que normalmente la suma se aproxima usando una suma parcial. Al hacerlo, nos interesa la cantidad de error en nuestra aproximación. Considerar una serie alterna

\[\sum_{n=1}^∞(−1)^{n+1}b_n \nonumber \]

satisfaciendo las hipótesis de la prueba de series alternas. Dejar\( S\) denotar la suma de esta serie y\( {S_k}\) ser la secuencia correspondiente de sumas parciales. De la Figura\( \PageIndex{2}\), vemos que para cualquier entero\( N≥1\), el resto\( R_N\) satisface

\[|R_N|=|S−S_N|≤|S_{N+1}−S_N|=b_{n+1}. \nonumber \]

Restos en serie alterna

Considere una serie alterna de la forma

\[\sum_{n=1}^∞(−1)^{n+1}b_n \nonumber \]o\[\sum_{n=1}^∞(−1)^nb_n \nonumber \]

que satisfaga las hipótesis de la prueba de series alternas. Dejar\( S\) denotar la suma de la serie y\( S_N\) denotar la suma\(N^{\text{th}}\) parcial. Para cualquier entero\( N≥1\), el resto\( R_N=S−S_N\) satisface

\[|R_N|≤b_{N+1}. \nonumber \]

Es decir, si se aplican las condiciones de la prueba de series alternas, entonces el error al aproximar la serie infinita por la suma\(N^{\text{th}}\) parcial\( S_N\) es en magnitud como máximo el tamaño del siguiente término\( b_{N+1}\).

Ejemplo\( \PageIndex{2}\): Estimating the Remainder of an Alternating Series

Considere las series alternas

\[ \sum_{n=1}^∞\dfrac{(−1)^{n+1}}{n^2}. \nonumber \]

Utilice la estimación del resto para determinar un límite sobre el error\( R_{10}\) si aproximamos la suma de la serie por la suma parcial\( S_{10}\).

Solución

Del teorema expuesto anteriormente,\[ |R_{10}|≤b_{11}=\dfrac{1}{11^2}≈0.008265. \nonumber \]

Ejercicio\(\PageIndex{2}\)

Encuentra un límite para\( R_{20}\) al aproximar\(\displaystyle \sum^∞_{n=1}\frac{(−1)^{n+1}}{n}\) por\( S_{20}\).

Pista

\( |R_{20}|≤b_{21}\)

Contestar

\( 0.04762\)

Convergencia absoluta y condicional

Considera una serie\(\displaystyle \sum_{n=1}^∞a_n\) y la serie relacionada\(\displaystyle \sum_{n=1}^∞|a_n|\). Aquí discutimos las posibilidades para la relación entre la convergencia de estas dos series. Por ejemplo, considere la serie armónica alterna\(\displaystyle \sum_{n=1}^∞\frac{(−1)^{n+1}}{n}\). La serie cuyos términos son el valor absoluto de estos términos es la serie armónica, ya que\(\displaystyle \sum_{n=1}^∞\left|\frac{(−1)^{n+1}}{n}\right|=\sum_{n=1}^∞\frac{1}{n}.\) Dado que la serie armónica alterna converge, pero la serie armónica diverge, decimos que la serie armónica alterna exhibe convergencia condicional.

Por comparación, considere la serie\(\displaystyle \sum_{n=1}^∞\frac{(−1)^{n+1}}{n^2}.\) La serie cuyos términos son los valores absolutos de los términos de esta serie es la serie\(\displaystyle \sum_{n=1}^∞\frac{1}{n^2}.\) Dado que ambas series convergen, decimos que la serie\(\displaystyle \sum_{n=1}^∞\frac{(−1)^{n+1}}{n^2}\) exhibe convergencia absoluta.

Definición: Convergencia Absoluta

Una serie\(\displaystyle \sum^∞_{n=1}a_n\) exhibe convergencia absoluta si\(\displaystyle \sum^∞_{n=1}|a_n|\) converge. Una serie\(\displaystyle \sum^∞_{n=1}a_n\) exhibe convergencia condicional si\(\displaystyle \sum^∞_{n=1}a_n\) converge pero\(\displaystyle \sum^∞_{n=1}|a_n|\) diverge.

Como lo muestra la serie armónica alterna, una serie\(\displaystyle \sum^∞_{n=1}a_n\) puede converger, pero\(\displaystyle \sum^∞_{n=1}|a_n|\) puede divergir. En el siguiente teorema, sin embargo, mostramos que si\(\displaystyle \sum^∞_{n=1}|a_n|\) converge, entonces\(\displaystyle \sum^∞_{n=1}a_n\) converge.

Convergencia absoluta implica convergencia

Si\(\displaystyle \sum^∞_{n=1}|a_n|\) converge, entonces\(\displaystyle \sum^∞_{n=1}a_n\) converge.

Prueba

Supongamos que eso\(\displaystyle \sum_{n=1}^∞|a_n|\) converge. Demostramos esto utilizando el hecho de que\( a_n=|a_n\) o\( a_n=−|a_n|\) y por lo tanto\( |a_n|+a_n=2|a_n|\) o\( |a_n|+a_n=0\). Por lo tanto,\( 0≤|a_n|+a_n≤2|a_n|\). En consecuencia, por la prueba de comparación, ya que\( 2\sum^∞_{n=1}|a_n|\) converge, la serie

\[\sum_{n=1}^∞(|a_n|+a_n) \nonumber \]

converge. Al usar las propiedades algebraicas para series convergentes, concluimos que

\[\sum_{n=1}^∞a_n=\sum_{n=1}^∞(|a_n|+a_n)−\sum_{n=1}^∞|a_n| \nonumber \]

converge.

□

Ejemplo\( \PageIndex{3}\): Absolute versus Conditional Convergence

Para cada una de las siguientes series, determine si la serie converge absolutamente, converge condicionalmente o diverge.

1. \(\displaystyle \sum^∞_{n=1}\frac{(−1)^{n+1}}{3n+1}\)
2. \(\displaystyle \sum^∞_{n=1}\frac{\cos(n)}{n^2}\)

Solución

a. Podemos ver que

\(\displaystyle \sum_{n=1}^∞\left|\dfrac{(−1)^{n+1}}{3n+1}\right|=\sum_{n=1}^∞\dfrac{1}{3n+1}\)

diverge mediante el uso de la prueba de comparación de límites con la serie armónica. De hecho,

\(\displaystyle \lim_{n→∞}\dfrac{1/(3n+1)}{1/n}=\dfrac{1}{3}\).

Por lo tanto, la serie no converge absolutamente. Sin embargo, desde

\( \dfrac{1}{3(n+1)+1}<\dfrac{1}{3n+1}\)y\( \dfrac{1}{3n+1}→0\),

la serie converge. Podemos concluir que\(\displaystyle \sum^∞_{n=1}\frac{(−1)^{n+1}}{3n+1}\) converge condicionalmente.

b. Observando que\( |\cos n|≤1,\) para determinar si la serie converge absolutamente, compare

\(\displaystyle \sum_{n=1}^∞\left|\dfrac{\cos n}{n^2}\right|\)

con la serie\(\displaystyle \sum^∞_{n=1}\frac{1}{n^2}\). Ya que\(\displaystyle \sum^∞_{n=1}\frac{1}{n^2}\) converge, por la prueba de comparación,\(\displaystyle \sum^∞_{n=1}\left|\frac{\cos n}{n^2}\right|\) converge, y por lo tanto\(\displaystyle \sum^∞_{n=1}\frac{\cos n}{n^2}\) converge absolutamente.

Ejercicio\(\PageIndex{3}\)

Determinar si la serie\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{n}{2n^3+1}\) converge absolutamente, converge condicionalmente o diverge.

Pista

Verifique primero la convergencia absoluta.

Contestar

La serie converge absolutamente.

Para ver la diferencia entre convergencia absoluta y condicional, mira lo que sucede cuando reorganizamos los términos de la serie armónica alterna\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{1}{n}\). Demostramos que podemos reorganizar los términos para que la nueva serie diverja. Ciertamente si reorganizamos los términos de una suma finita, la suma no cambia. Cuando trabajamos con una suma infinita, sin embargo, pueden suceder cosas interesantes.

Comience por agregar suficientes términos positivos para producir una suma que sea mayor que algún número real\( M=10\) Por ejemplo, let\( M=10,\) and find a integer\( k\) such that

\[1+\dfrac{1}{3}+\dfrac{1}{5}+⋯+\dfrac{1}{2k−1}>10 \nonumber \]

(Podemos hacer esto porque la serie\(\displaystyle \sum^∞_{n=1}\frac{1}{2n−1}\) diverge hasta el infinito.) Después restar\( 1/2\). Después agregue términos más positivos hasta que la suma llegue a 100. Es decir, encontrar otro entero\( j>k\) tal que

\[(1+\dfrac{1}{3}+⋯+\dfrac{1}{2k−1}−\dfrac{1}{2}+\dfrac{1}{2k+1}+ \ldots +\dfrac{1}{2j+1}>100. \nonumber \]

Después restar\( 1/4.\) Continuando de esta manera, hemos encontrado una manera de reordenar los términos en las series armónicas alternas para que la secuencia de sumas parciales para la serie reordenada quede sin límites y por lo tanto diverja.

Los términos de la serie armónica alterna también se pueden reordenar para que la nueva serie converja a un valor diferente. En Ejemplo, mostramos cómo reorganizar los términos para crear una nueva serie a la que converja\( 3\ln(2)/2\). Señalamos que las series armónicas alternas pueden reorganizarse para crear una serie que converja a cualquier número real\( r\); sin embargo, la prueba de ese hecho está más allá del alcance de este texto.

En general, cualquier serie\(\displaystyle \sum^∞_{n=1}a_n\) que converja condicionalmente puede ser reordenada para que la nueva serie diverja o converja a un número real diferente. Una serie que converge absolutamente no tiene esta propiedad. Para cualquier serie\(\displaystyle \sum^∞_{n=1}a_n\) que converja absolutamente, el valor de\(\displaystyle \sum^∞_{n=1}a_n\) es el mismo para cualquier reordenamiento de los términos. Este resultado es conocido como el Teorema del Reordenamiento de Riemann, que está más allá del alcance de este libro.

Ejemplo\( \PageIndex{4}\): Rearranging Series

Usa el hecho de que

\[ 1−\dfrac{1}{2}+\dfrac{1}{3}−\dfrac{1}{4}+\dfrac{1}{5}−⋯=\ln 2 \nonumber \]

para reorganizar los términos en la serie armónica alterna para que la suma de la serie reordenada sea\( 3\ln (2)/2.\)

Solución

Let

\[ \sum_{n=1}^∞a_n=1−\dfrac{1}{2}+\dfrac{1}{3}−\dfrac{1}{4}+\dfrac{1}{5}−\dfrac{1}{6}+\dfrac{1}{7}−\dfrac{1}{8}+⋯. \nonumber \]

Dado que\(\displaystyle \sum_{n=1}^∞a_n=\ln (2)\), por las propiedades algebraicas de las series convergentes,

\[ \sum_{n=1}^∞\dfrac{1}{2}a_n=\dfrac{1}{2}−\dfrac{1}{4}+\dfrac{1}{6}−\dfrac{1}{8}+⋯=\dfrac{1}{2}\sum_{n=1}^∞a_n=\dfrac{\ln 2}{2}. \nonumber \]

Ahora introduce la serie\(\displaystyle \sum_{n=1}^∞b_n\) tal que para todos\( n≥1, b_{2n−1}=0\) y\( b_{2n}=a_n/2.\) Entonces

\[ \sum_{n=1}^∞b_n=0+\dfrac{1}{2}+0−\dfrac{1}{4}+0+\dfrac{1}{6}+0−\dfrac{1}{8}+⋯=\dfrac{\ln 2}{2}. \nonumber \]

Luego usando las propiedades límite algebraicas de las series convergentes, ya que\(\displaystyle \sum_{n=1}^∞a_n\) y\(\displaystyle \sum_{n=1}^∞b_n\) convergen, la serie\(\displaystyle \sum_{n=1}^∞(a_n+b_n)\) converge y

\[ \sum_{n=1}^∞(a_n+b_n)=\sum_{n=1}^∞a_n+\sum_{n=1}^∞b_n=\ln 2+\dfrac{\ln 2}{2}=\dfrac{3\ln 2}{2}. \nonumber \]

Ahora sumando los términos correspondientes\( b_n\),\( a_n\) y, vemos que

\[ \sum_{n=1}^∞(a_n+b_n)=(1+0)+\left(−\dfrac{1}{2}+\dfrac{1}{2}\right)+\left(\dfrac{1}{3}+0\right)+\left(−\dfrac{1}{4}−14\right)+\left(\dfrac{1}{5}+0\right)+\left(−\dfrac{1}{6}+\dfrac{1}{6}\right)+\left(\dfrac{1}{7}+0\right)+\left(\dfrac{1}{8}−\dfrac{1}{8}\right)+⋯=1+\dfrac{1}{3}−\dfrac{1}{2}+\dfrac{1}{5}+\dfrac{1}{7}−\dfrac{1}{4}+⋯. \nonumber \]

Observamos que la serie en el lado derecho del signo igual es un reordenamiento de la serie armónica alterna. Desde que\(\displaystyle \sum_{n=1}^∞(a_n+b_n)=3\ln (2)/2,\) concluimos que

\[ 1+\dfrac{1}{3}−\dfrac{1}{2}+\dfrac{1}{5}+\dfrac{1}{7}−\dfrac{1}{4}+⋯=\dfrac{3\ln (2)}{2}. \nonumber \]

Por lo tanto, hemos encontrado un reordenamiento de la serie armónica alterna que tiene la propiedad deseada.

Conceptos clave

• Para una serie alterna\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}b_n,\) si\( b_{k+1}≤b_k\) para todos\( k\) y\( b_k→0\) como\( k→∞,\) la serie alterna converge.
• Si\(\displaystyle \sum^∞_{n=1}|a_n|\) converge, entonces\(\displaystyle \sum^∞_{n=1}a_n\) converge.

Ecuaciones Clave

• Serie alternada

\(\displaystyle \sum_{n=1}^∞(−1)^{n+1}b_n=b_1−b_2+b_3−b_4+⋯\)o

\(\displaystyle \sum_{n=1}^∞(−1)^nb_n=−b_1+b_2−b_3+b_4−⋯\)

Glosario

convergencia absoluta

si la serie\(\displaystyle \sum^∞_{n=1}|a_n|\) converge,\(\displaystyle \sum^∞_{n=1}a_n\) se dice que la serie converge absolutamente

series alternas

una serie de la forma\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}b_n\) o\(\displaystyle \sum^∞_{n=1}(−1)^nb_n\), donde\( b_n≥0\), se llama una serie alterna

prueba en serie alterna

para una serie alterna de cualquier forma, si\( b_{n+1}≤b_n\) para todos los enteros\( n≥1\) y\( b_n→0\), entonces una serie alterna converge

convergencia condicional

si la serie\(\displaystyle \sum^∞_{n=1}a_n\) converge, pero la serie\(\displaystyle \sum^∞_{n=1}|a_n|\) diverge,\(\displaystyle \sum^∞_{n=1}a_n\) se dice que la serie converge condicionalmente