3.5: Cambio de Variables en Integrales Múltiples
- Page ID
- 111257
Dada la dificultad de evaluar múltiples integrales, el lector puede preguntarse si es posible simplificar esas integrales usando una sustitución adecuada para las variables. La respuesta es sí, aunque es un poco más complicado que el método de sustitución que aprendiste en el cálculo de una sola variable.
Recordemos que si se le da, por ejemplo, la integral definitiva
\[ \int_1^2 x^3 \sqrt{x^2-1}\,dx \]
entonces harías la sustitución
\[\begin{align} u &= x^2-1 \Rightarrow x^2=u+1 \\[4pt] \nonumber du &= 2x\,dx \end{align}\]
que cambia los límites de la integración
\[ \begin{align} x &=1 \Rightarrow u=0 \\[4pt] \nonumber x&=2 \Rightarrow u=3 \end{align}\]
para que consigamos
\[\nonumber \begin{align} \int_1^2 x^3 \sqrt{x^2-1} &= \int_1^2 \dfrac{1}{2}x^2 \cdot 2x\sqrt{x^2-1}\,dx \\[4pt] \nonumber &=\int_0^3 \dfrac{1}{2}(u+1)\sqrt{u}\,du \\[4pt] \nonumber &=\dfrac{1}{2}\int_0^3 \left ( u^{3/2}+u^{1/2} \right )\,du,\text{ which can be easily integrated to give} \\[4pt] \nonumber &=\dfrac{14\sqrt{3}}{5} \end{align} \]
Echemos un vistazo diferente a lo que sucedió cuando hicimos esa sustitución, lo que dará cierta motivación para cómo funciona la sustitución en múltiples integrales. Primero, dejamos\(u = x^2 − 1\). En el intervalo de integración\([1,2]\), la función\(x \mapsto x^2 −1\) es estrictamente creciente (y mapea\([1,2] \text{ onto }[0,3])\) y por lo tanto tiene una función inversa (definida en el intervalo\([0,3]\)). Es decir, en\([0,3]\) podemos definir\(x\text{ as a function of }u\), a saber
\[x=g(u) = \sqrt{u+1}\]
Luego sustituyendo esa expresión por\(x\) en la función\(f (x) = x^3 \sqrt{x^2 −1}\) da
\[ f (x) = f (g(u)) = (u +1)^{3/2}\sqrt{u}\]
y vemos que
\[ \begin{align} \dfrac{dx}{du} = g'(u) \Rightarrow dx &= g'(u)\,du \\[4pt] \nonumber dx &= \dfrac{1}{2}(u+1)^{-1/2}\,du \end{align}\]
así que desde
\[ \begin{align} g(0) = 1 \Rightarrow 0 &=g^{-1}(1) \\[4pt] \nonumber g(3) =2 \Rightarrow 3 &= g^{-1}(2) \end{align}\]
luego realizar la sustitución como hicimos antes da
\[ \begin{align} \int_1^2 f(x)\,dx &= \int_1^2 x^3 \sqrt{x^2-1}\,dx \\[4pt] \nonumber &=\int_0^3 \dfrac{1}{2}(u+1)\sqrt{u}\,du,\text {which can be written as} \\[4pt] \nonumber &=\int_0^3 (u+1)^{3/2}\sqrt{u}\cdot \dfrac{1}{2}(u+1)^{-1/2}\,du, \text{ which means} \\[4pt] \nonumber \int_1^2 f(x)\,dx &= \int_{g^{-1}(1)}^{g^{-1}(2)} f(g(u))g'(u)\,du \end{align}\]
En general, si\(x = g(u)\) es una función uno-a-uno, diferenciable de un intervalo\([c,d]\) (que se puede pensar que está en el “\(u\)eje”) a un intervalo\([a,b]\) (en el\(x\) eje -), lo que significa que\(g′(u) \neq 0\) en el intervalo\((c,d)\), así que\(a = g(c)\text{ and }b = g(d),\text{ then }c = g^{ −1} (a)\text{ and }d = g^{−1} (b)\), y
\[\int_a^b f(x)\,dx = \int_{g^{-1}(a)}^{g^{-1}(b)} f(g(u))g'(u)\,du \label{Eq3.17}\]
Esto se llama fórmula de cambio de variable para integrales de funciones de variable única, y es lo que estabas usando implícitamente al hacer integración por sustitución. Esta fórmula resulta ser un caso especial de una fórmula más general que se puede utilizar para evaluar múltiples integrales. Estableceremos las fórmulas para integrales dobles y triples que involucran funciones de valor real de dos y tres variables, respectivamente. Asumiremos que todas las funciones involucradas son continuamente diferenciables y que las regiones y los sólidos involucrados tienen límites “razonables”. La prueba del siguiente teorema está fuera del alcance del texto.
Teorema\(\PageIndex{1}\): Change of Variables Formula for Multiple Integrals
Vamos a\(x = x(u,v) \text{ and }y = y(u,v)\) definir un mapeo uno a uno de una región\(R ′\) en el\(uv\) plano -sobre una región\(R\) en el\(x y\) -plano tal que el determinante
\[J(u,v) = \begin{vmatrix} \dfrac{∂x}{∂u} & \dfrac{∂x}{∂v} \\[4pt] \dfrac{∂y}{∂u} & \dfrac{∂y}{∂v}\\[4pt] \end{vmatrix} \label{Eq3.18}\]
nunca está en\(R'\). Entonces
\[\iint\limits_R f (x, y)\,d A(x, y) = \iint\limits_{R'}f (x(u,v), y(u,v))\,|J(u,v)|\,d A(u,v)\label{Eq3.19}\]
Utilizamos la notación\(d A(x, y)\) y\(d A(u,v)\) para denotar el elemento area en las\((x, y)\text{ and }(u,v)\) coordenadas, respectivamente.
Del mismo modo, si se\(x = x(u,v,w), y = y(u,v,w) \text{ and }z = z(u,v,w)\) define un mapeo uno a uno de un sólido\(S′\) en\(uvw\) el espacio sobre un\(S \text{ in }x yz\) espacio sólido tal que el determinante
\[J(u,v,w) = \begin{vmatrix} \dfrac{∂x}{∂u} & \dfrac{∂x}{∂v} & \dfrac{∂x}{∂w} \\[4pt] \dfrac{∂y}{∂u} & \dfrac{∂y}{∂v} & \dfrac{∂y}{∂w} \\[4pt] \dfrac{∂z}{∂u} & \dfrac{∂z}{∂v} & \dfrac{∂z}{∂w} \\[4pt] \end{vmatrix} \label{Eq3.20}\]
nunca es 0 en\(S'\), entonces
\[\iiint\limits_S f (x, y, z)dV(x, y, z) = \iiint\limits_{S'}f (x(u,v,w), y(u,v,w), z(u,v,w))|J(u,v,w)|dV (u,v,w) \label{Eq3.21}\]
El determinante\(J(u,v)\) en la Ecuación\ ref {Eq3.18} se llama jacobiano de\(x \text{ and }y \text{ with respect to }u \text{ and }v\), y a veces se escribe como
\[J(u,v) = \dfrac{∂(x, y)}{∂(u,v)}\label{Eq3.22}\]
Del mismo modo, el jacobiano\( J(u,v,w)\) de tres variables a veces se escribe como
\[J(u,v,w) = \dfrac{∂(x, y, z)}{∂(u,v,w)} \label{Eq3.23}\]
Observe que Ecuación\ ref {Eq3.19} está diciendo eso\(d A(x, y) = |J(u,v)|d A(u,v)\), que se puede pensar como una versión de dos variables de la relación\(dx = g ′ (u)\,du\) en el caso de una sola variable.
El siguiente ejemplo muestra cómo se utiliza la fórmula de cambio de variables.
Ejemplo\(\PageIndex{1}\)
Evaluar
\[\nonumber \iint _R e^{\frac{x-y}{x+y}}\,dA\]
donde\(R= {(x, y) : x ≥ 0, y ≥ 0, x+ y ≤ 1}\).
Solución
Primero, tenga en cuenta que evaluar esta doble integral sin usar la sustitución es probablemente imposible, al menos en forma cerrada. Al mirar el numerador y denominador del exponente de\(e\), intentaremos la sustitución\(u = x − y \text{ and }v = x + y\). Para usar el cambio de variables Fórmula\ ref {Eq3.19}, necesitamos escribir ambas\(x \text{ and }y\) en términos de\(u \text{ and }v\). Entonces resolviendo para\(x \text{ and }y\) da\(x = \dfrac{1}{2} (u + v) \text{ and }y = \dfrac{1}{ 2} (v − u)\). En la Figura\(\PageIndex{1}\) a continuación, vemos cómo el mapeo\(x = x(u,v) = \dfrac{1}{ 2} (u+v), y = y(u,v) = \dfrac{1}{ 2} (v− u)\) mapea la región\(R′\)\(R\) en una manera uno a uno.
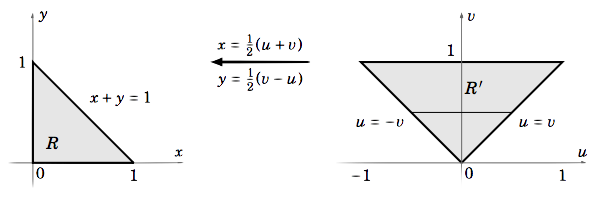
Ahora vemos que
\[\nonumber J(u,v) = \begin{vmatrix} \dfrac{∂x}{∂u} & \dfrac{∂x}{∂v} \\[4pt] \dfrac{∂y}{∂u} & \dfrac{∂y}{∂v} \\[4pt] \end{vmatrix} = \begin{vmatrix} \dfrac{1}{2} & \dfrac{1}{2} \\[4pt] -\dfrac{1}{2} & \dfrac{1}{2} \\[4pt] \end{vmatrix} = \dfrac{1}{2} \Rightarrow \lvert J(u,v) \rvert = \left\lvert \dfrac{1}{2} \right\rvert=\dfrac{1}{2} \]
así que usando rebanadas horizontales en\(R'\), tenemos
\[\nonumber \begin{align} \iint\limits_R e^{\dfrac{x-y}{x+y}}\,dA &= \iint\limits_{R'}f (x(u,v), y(u,v))|J(u,v)|d A \\[4pt] \nonumber &=\int_0^1 \int_{-v}^v e^{u/v}\dfrac{1}{2}\,du\,dv \\[4pt] \nonumber &= \int_0^1 \left ( \dfrac{v}{2}e^{u/v} \big |_{u=-v}^{u=v} \right ) dv \\[4pt] \nonumber &=\int_0^1 \dfrac{v}{2}(e-e^1)dv \\[4pt] \nonumber &=\dfrac{v^2}{4}(e-e^1)\big |_0^1 = \dfrac{1}{4} \left ( e-\dfrac{1}{e} \right ) = \dfrac{e^2-1}{4e} \end{align}\]
La fórmula de cambio de variables se puede utilizar para evaluar integrales dobles en coordenadas polares. Dejar
\[ x = x(r,θ) = r \cos{θ} \text{ and }y = y(r,θ) = r \sin{θ} , \]
tenemos
\[ J(u,v) = \begin{vmatrix} \dfrac{∂x}{∂r} & \dfrac{∂x}{∂θ} \\[4pt] \dfrac{∂y}{∂r} & \dfrac{∂y}{∂θ} \\[4pt] \end{vmatrix} = \begin{vmatrix} \cos{θ} & -r \sin{θ} \\[4pt] \sin{θ} & r\cos{θ} \end{vmatrix} = r \cos^2{ θ} + r \sin^2 {θ} = r \Rightarrow |J(u,v)| = |r| = r \]
por lo que tenemos la siguiente fórmula:
Doble Integral en Coordenadas Polares
\[\iint\limits_R f (x, y)\,dx\, d y = \iint\limits_{R'}f (r \cos{θ}, r \sin{θ}) r\, dr\, dθ \label{Eq3.24}\]
donde el mapeo\(x = r \cos{θ}, y = r \sin{θ}\) mapea la región\(R′\) en el\(rθ\) plano -sobre la región\(R\) en el\(x y\) plano -de una manera uno a uno.
Ejemplo\(\PageIndex{2}\): Volume of Paraboloid
Encuentra el volumen\(V\) dentro del paraboloide\(z = x^ 2 + y^ 2 \text{ for }0 ≤ z ≤ 1\)
Solución
Usando rebanadas verticales, vemos que
\[\nonumber V= \iint\limits_R (1− z)d A = \iint\limits_R ( 1−(x^2 + y^ 2)) d A \]
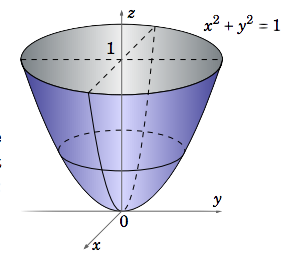
donde\(R = {(x, y) : x^ 2 + y^ 2 ≤ 1}\) se encuentra el disco de la unidad\(\mathbb{R}^2\) (ver Figura\(\PageIndex{2}\)). En coordenadas polares lo\((r,θ)\) sabemos\(x^ 2+ y^ 2 = r^ 2\) y que el disco unitario\(R\) es el conjunto\(R ′ = {(r,θ) : 0 ≤ r ≤ 1,0 ≤ θ ≤ 2\pi}\). Por lo tanto,
\[\nonumber \begin{align} V &= \int_0^{2\pi} \int_0^1 (1− r^ 2 ) r\, dr\, dθ \\[4pt] \nonumber &= \int_0^{2\pi} \int_0^1 (r − r^ 3 )dr\, dθ \\[4pt] \nonumber &= \int_o^{2\pi} \left ( \dfrac{r^2}{2}-\dfrac{r^4}{4}\big |_{r=0}^{r=1} \right )\,dθ \\[4pt] \nonumber &= \int_0^{2\pi}\dfrac{1}{4}\,dθ \\[4pt] \nonumber &=\dfrac{\pi}{2} \end{align}\]
Ejemplo\(\PageIndex{3}\): Volume of Cone
Encuentra el volumen\(V\) dentro del cono\(z = \sqrt{ x^ 2 + y^ 2}\text{ for }0 ≤ z ≤ 1\).
Solución
Usando rebanadas verticales, vemos que
\[\nonumber V= \iint\limits_R (1− z)d A = \iint\limits_R \left ( 1−\sqrt{x^2 + y^ 2}\right ) d A\]
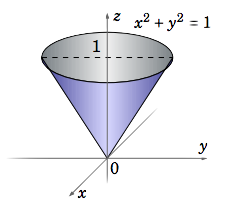
donde\(R = {(x, y) : x^ 2 + y^ 2 ≤ 1}\) se encuentra el disco de la unidad\(\mathbb{R}^2\) (ver Figura\(\PageIndex{3}\)). En coordenadas polares lo\((r,θ)\) sabemos\(\sqrt{x^ 2 + y^ 2 = r}\) y que el disco unitario\(R\) es el conjunto\(R ′ = {(r,θ) : 0 ≤ r ≤ 1,0 ≤ θ ≤ 2\pi}\). Por lo tanto,
\[\nonumber \begin{align} V &= \int_0^{2\pi}\int_0^1(1− r) r\, dr\, dθ \\[4pt] \nonumber &=\int_0^{2\pi}\int_0^1(r − r^ 2 )dr\, dθ \\[4pt] \nonumber &=\int_0^{2\pi} \left ( \dfrac{r^2}{2}-\dfrac{r^3}{3}\big |_{r=0}^{r=1} \right )dθ \\[4pt] \nonumber &= \int_0^{2\pi} \dfrac{1}{6}dθ \\[4pt] \nonumber &=\dfrac{\pi}{3} \end{align} \]
De manera similar, se puede demostrar (ver Ejercicios 5-6) que las integrales triples en coordenadas cilíndricas y esféricas toman las siguientes formas:
Triple Integral en Coordenadas Cilíndricas
\[\iiint\limits_S f (x, y, z)dx\, d y\, dz =\iiint\limits_{S'} (r \cos{θ}, r \sin{θ}, z) r\, dr\, dθ\, dz \label{Eq3.25}\]
donde el mapeo\(x = r \cos{θ}, y = r \sin{θ}, z = z\) mapea el sólido\(S ′\) en el\(rθz\) espacio sobre el\(S \text{ in }x yz\) espacio sólido de una manera uno a uno.
Triple Integral en Coordenadas Esféricas
\[\iiint\limits_S f (x, y, z)dx\, d y\, dz = \iiint\limits_{S'}f (ρ \sin{φ} \cos{θ},ρ \sin{φ} \sin{θ},ρ \cos{φ})ρ^2 \sin{φ}dρ\, dφ\,dθ \label{Eq3.26}\]
donde el mapeo\(x = ρ \sin{φ} \cos{θ}, y = ρ \sin{φ} \sin{θ}, z = ρ \cos{φ} \) mapea el sólido\(S ′\) en\(ρφθ\) el espacio sobre el sólido\(S\) en el\(x yz\) espacio de una manera uno a uno.
Ejemplo\(\PageIndex{4}\)
Pues\(a > 0\), encuentra el volumen\(V\) dentro de la esfera\(S = x^ 2 + y^ 2 + z^ 2 = a^ 2\).
Solución
Vemos que\(S\) es el conjunto\(ρ = a\) en coordenadas esféricas, entonces
\[\nonumber \begin{align} V&=\iiint\limits_S 1dV = \int_0^{2\pi}\int_0^{\pi}\int_0^a 1ρ^2 \sin{φ}dρ\, dφ\,dθ \\[4pt] \nonumber &= \int_0^{2\pi}\int_0^{\pi} \left ( \dfrac{ρ^ 3}{3}\big |_{ρ=0}^{ρ=a} \right ) \sin{φ}dφ\,dθ = \int_0^{2\pi}\int_0^{\pi}\dfrac{a^3}{3}\sin{φ}dφ\,dθ \\[4pt] \nonumber &=\int_0^{2\pi} \left (-\dfrac{a^3}{3}\cos{φ}\big |_{φ=0}^{ φ=π} \right )dθ = \int_0^{2\pi} \dfrac{2a^3}{3}dθ = \dfrac{4\pi a^3}{3}\end{align}\]