Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

3.4: Encontrar soluciones imaginarias

Última actualización

30 oct 2022
Guardar como PDF
- 3.3: Teorema del Valor Intermedio, Existencia de Solución
- 4: Diferenciación - Modelos de Pendiente usando Derivadas

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Louis calcula que el área de un rectángulo está representada por la ecuación 3x ⁴ + 7x ² = 2. ¿Louis lo calculó bien? Explicar con base en el grado y ceros de la función.

Soluciones imaginarias

Recuerda, las soluciones imaginarias siempre vienen en parejas. Para encontrar las soluciones imaginarias a una función, utilice la Fórmula Cuadrática.

Resolvamos f (x) =3x ⁴ −x ² −14.

En primer lugar, esta función cuártica se puede factorizar igual que una ecuación cuadrática.

g (x) =x ⁴ +21x ² +90

Ahora bien, debido a que ninguno de los factores se puede factorizar más y no hay x−term, podemos establecer cada uno igual a cero y resolver.

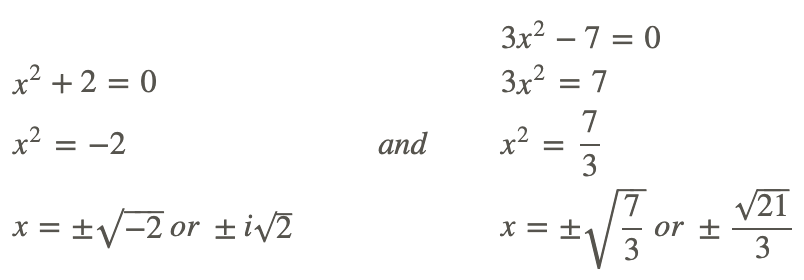
Screen Shot 2020-09-25 at 1.54.11 PM.png

Incluyendo las soluciones imaginarias, hay cuatro, que es lo que esperaríamos porque el grado de esta función es cuatro.

Ahora, vamos a encontrar todas las soluciones de la función g (x) =x ⁴ +21x ² +90.

Cuando se grafica, esta función no toca el eje x. Por lo tanto, todas las soluciones son imaginarias. Para resolver, esta función se puede factorizar como una ecuación cuadrática. Los factores de 90 que suman 21 son 6 y 15.

g (x) 0=x ⁴ +21x ² +9

0= (x ² +6) (x ² +15)

Ahora, establezca cada factor igual a cero y resuelva.

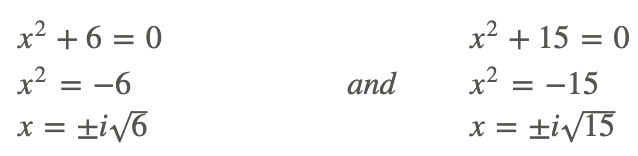
Screen Shot 2020-09-25 a las 2.01.00 PM.png

Por último, encontremos la función que tiene la solución 3, -2 y 4+i.

Observe que una de las soluciones dadas implica un número imaginario. Las soluciones imaginarias y complejas siempre vienen en pares, por lo que 4−i también es un factor. Los dos factores son conjugados complejos. Traduzca cada solución en un factor y multiplíquelas todas juntas.

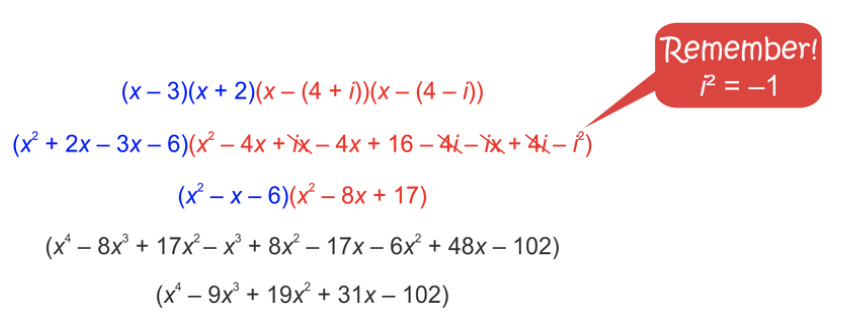
Screen Shot 2020-09-25 a las 2.06.34 PM.png

Bahman Kalantari - https://commons.wikimedia.org/wiki/File%3ANonfractal_polynomiograph.png

Cualquier múltiplo de esta función también tendría estas raíces. Por ejemplo, 2x4−18x3+38x2+62x−204 también tendría estas raíces.

Ejemplos

Ejemplo 1

Anteriormente, se le pidió que determinara si Louis calculó correctamente su trabajo.

Primero tenemos que cambiar la ecuación a la forma estándar. Entonces podemos factorizarlo.

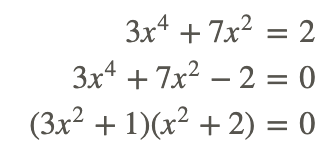
Screen Shot 2020-09-25 a las 2.21.22 PM.png

Resolviendo para x obtenemos

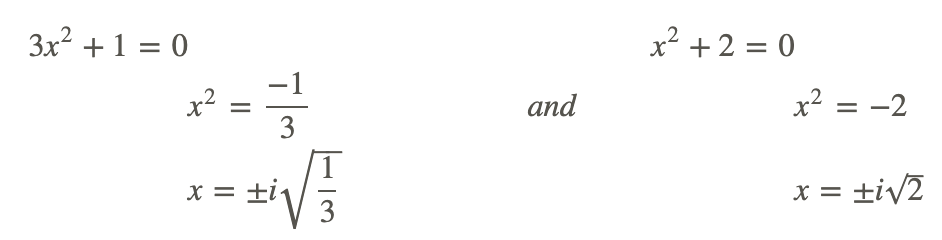
Screen Shot 2020-09-25 at 2.49.38 PM.png

Todas las soluciones son imaginarias y el área de un rectángulo debe tener soluciones reales. Por lo tanto Louis no calculó correctamente.

Ejemplo 2

Encuentre todas las soluciones a la siguiente función: f (x) =25x3−120x2+81x−4.

Primero, grafica la función.

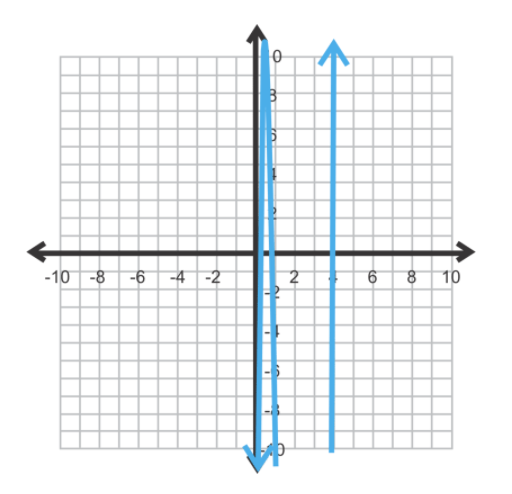
Screen Shot 2020-09-25 at 3.02.33 PM.png

Usando el Teorema de la Raíz Racional, los posibles ceros realistas podrían ser ¹/₂₅, 1 o 4. Probemos estas tres posibilidades usando división sintética.

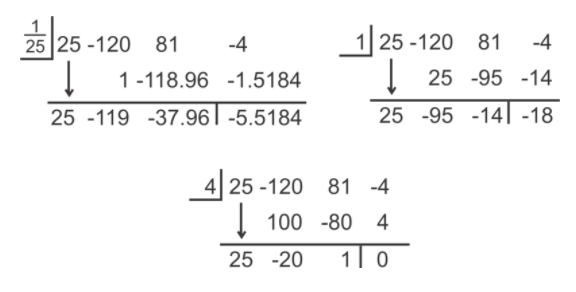
Screen Shot 2020-09-26 at 3.00.00 PM.png

De estas tres posibilidades, sólo 4 es un cero. El polinomio sobrante, 25x ² −20x+1 no es factorizable, por lo que necesitamos usar la Fórmula Cuadrática para encontrar los dos últimos ceros.

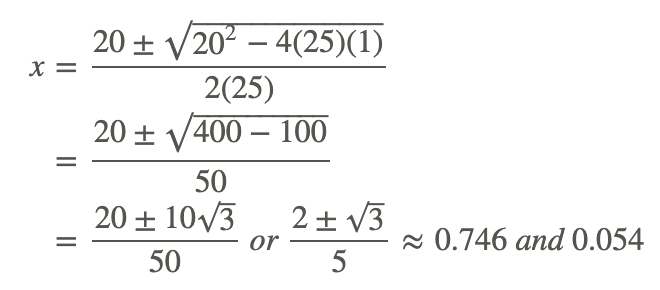
Screen Shot 2020-09-26 at 3.01.35 PM.png

Pista útil: Siempre encuentre los valores decimales de cada cero para asegurarse de que coincidan con la gráfica.

Ejemplo 3

Encuentra todas las soluciones a la siguiente función: f (x) =4x ⁴ +35x ² −9.

f (x) =4x ⁴ +35x ² −9 es factorizable. ac=−36.

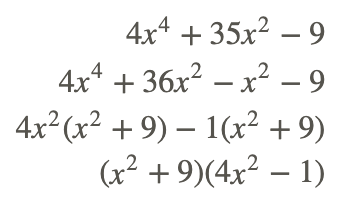
Screen Shot 2020-09-26 at 3.02.09 PM.png

Estableciendo cada factor igual a cero, tenemos:

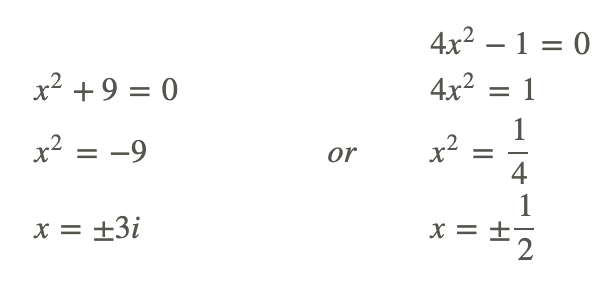
Screen Shot 2020-09-26 at 4.21.04 PM.png

Ejemplo 4

Encuentra la ecuación de una función con raíces 4, 2 ^0.5 y 1−i.

Recordemos que las raíces irracionales e imaginarias vienen en parejas. Por lo tanto, todas las raíces son 4, 2 ^0.5, −2 ^0.5 ,1+i,1−i. Multiplica las 5 raíces juntas.

Revisar

Encuentra todas las soluciones a las siguientes funciones. Utilice cualquier método.

f (x) =x ⁴ +x ³ −12x ² −10x+20
f (x) =4x ³ −20x ² −3x+15
f (x) =2x ⁴ −7x ² −30
f (x) =x ³ +5x ² +12x+18
f (x) =4x ⁴ +4x ³ −22x ² −8x+40
f (x) =3x ⁴ +4x ² −15
f (x) =2x ³ −6x ² +9x−27
f (x) =6x ⁴ −7x ³ −280x ² −419x+280
f (x) =9x ⁴ +6x ³ −28x ² +2x+11
f (x) =2x ⁵ −19x ⁴ +30x ³ +97x ² −20x+150

Encuentra una función con las siguientes raíces.

4, i
−3, −2i
5 ^0.5, −1+i
2,13,4−2 ^0,5
Redacción: Anota los pasos que usas para encontrar todos los ceros de una función polinómica.
Redacción: ¿Por qué las raíces imaginarias e irracionales siempre vienen en parejas?
Desafío: Encuentra todas las soluciones a f (x) =x5+x3+8x2+8.

Respuestas para problemas de revisión

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 6.12.

vocabulario

Término	Definición
Conjugado complejo	Los conjugados complejos son pares de binomios complejos. El complejo conjugado de a+bi es a-bi. Cuando se multiplican los conjugados complejos, el resultado es un solo número real.
número complejo	Un número complejo es la suma de un número real y un número imaginario, escritos en la forma a+bi.
teorema de pares conjugados	El teorema de pares conjugados establece que si f (z) es un polinomio de grado n, con n≠ 0 y con coeficientes reales, y si f (z0) =0, donde z0=a+bi, entonces f (z0) =0. Donde z 0 es el conjugado complejo de z0.
teorema fundamental de álgebra	El teorema fundamental del álgebra establece que si f (x) es un polinomio de grado n≥1, entonces f (x) tiene al menos un cero en el dominio numérico complejo. En otras palabras, hay al menos un número complejo c tal que f (c) =0. El teorema también se puede afirmar de la siguiente manera: un polinomio de enésimo grado con coeficientes reales o complejos tiene, con multiplicidad, exactamente n raíces complejas.
Número imaginario	Un número imaginario es un número que puede escribirse como producto de un número real e i.
Números imaginarios	Un número imaginario es un número que puede escribirse como producto de un número real e i.
Polinomio	Un polinomio es una expresión con al menos un término algebraico, pero que no indica división por una variable ni contiene variables con exponentes fraccionarios.
Raíces	Las raíces de una función son los valores de x que hacen y igual a cero.
Cero	Los ceros de una función f (x) son los valores de x que hacen que f (x) sea igual a cero.
Ceros	Los ceros de una función f (x) son los valores de x que hacen que f (x) sea igual a cero.

Recursos adicionales

PLIX: Juega, aprende, interactúa, explora - Ceros imaginarios

Video: Teorema Fundamental del Álgebra - Visión general

Práctica: Encontrar soluciones imaginarias