12.6: Superficies cuádricas

Última actualización
Guardar como PDF

Page ID: 116137

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

Identificar un cilindro como un tipo de superficie tridimensional.
Reconocer las principales características de elipsoides, paraboloides e hiperboloides.
Utilice trazas para dibujar las intersecciones de superficies cuádricas con los planos de coordenadas.

Hemos estado explorando vectores y operaciones vectoriales en el espacio tridimensional, y hemos desarrollado ecuaciones para describir líneas, planos y esferas. En esta sección, utilizamos nuestro conocimiento de planos y esferas, que son ejemplos de figuras tridimensionales llamadas superficies, para explorar una variedad de otras superficies que se pueden graficar en un sistema de coordenadas tridimensional.

Identificación de Cilindros

La primera superficie que examinaremos es el cilindro. Aunque la mayoría de la gente piensa inmediatamente en una pipa hueca o una pajita de soda cuando escuchan la palabra cilindro, aquí usamos el amplio significado matemático del término. Como hemos visto, las superficies cilíndricas no tienen que ser circulares. Un conducto de calentamiento rectangular es un cilindro, al igual que una esterilla de yoga arrollada, cuya sección transversal tiene forma de espiral.

En el plano de coordenadas bidimensionales, la ecuación$ x^2+y^2=9$ describe un círculo centrado en el origen con radio$ 3$. En el espacio tridimensional, esta misma ecuación representa una superficie. Imagine copias de un círculo apiladas una encima de la otra centrada en el$z$ eje -eje (Figura$\PageIndex{1}$), formando un tubo hueco. Entonces podemos construir un cilindro a partir del conjunto de líneas paralelas al$z$ eje -que pasa por el círculo$ x^2+y^2=9$ en el$xy$ plano -como se muestra en la figura. De esta manera, cualquier curva en uno de los planos de coordenadas se puede extender para convertirse en una superficie.

Esta figura es un sistema de coordenadas tridimensionales. Tiene un centro circular derecho con el eje z a través del centro. El cilindro también tiene puntos etiquetados en los ejes x e y en (3, 0, 0) y (0, 3, 0). — Figura$\PageIndex{1}$: En el espacio tridimensional, la gráfica de ecuación$ x^2+y^2=9$ es un cilindro con radio$ 3$ centrado en el$z$ eje. Continúa indefinidamente en las direcciones positiva y negativa.

Definición: cilindros y resoluciones

Un conjunto de líneas paralelas a una línea dada que pasa a través de una curva dada se conoce como superficie cilíndrica, o cilindro. A las líneas paralelas se les llama sentencias.

A partir de esta definición, podemos ver que todavía tenemos un cilindro en el espacio tridimensional, aunque la curva no sea un círculo. Cualquier curva puede formar un cilindro, y las reglas que componen el cilindro pueden ser paralelas a cualquier línea dada (Figura$\PageIndex{2}$).

Esta figura tiene una superficie tridimensional que comienza en el eje y y se curva hacia arriba. También están etiquetados los ejes x y z. — Figura$\PageIndex{2}$: En el espacio tridimensional, la gráfica de ecuación$ z=x^3$ es un cilindro, o una superficie cilíndrica con reglas paralelas al$y$ eje -eje.

Ejemplo$ \PageIndex{1}$: Graphing Cylindrical Surfaces

Esboce las gráficas de las siguientes superficies cilíndricas.

$ x^2+z^2=25$
$ z=2x^2−y$
$ y=\sin x$

Solución

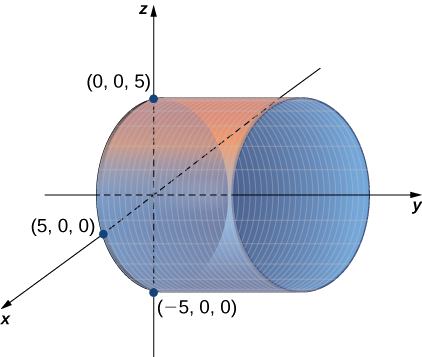
a. La variable$ y$ puede tomar cualquier valor sin límite. Por lo tanto, las líneas que gobierna esta superficie son paralelas al$y$ eje. La intersección de esta superficie con el$xz$ plano -forma un círculo centrado en el origen con radio$ 5$ (ver Figura$\PageIndex{3}$).

Esta figura es el sistema de coordenadas tridimensionales. Tiene un cilindro circular derecho en su costado con el eje y en el centro. El cilindro cruza el eje x en (5, 0, 0). También tiene dos puntos de intersección etiquetados en el eje z en (0, 0, 5) y (0, 0, -5). — Figura$\PageIndex{3}$: La gráfica de la ecuación$ x^2+z^2=25$ es un cilindro con radio$ 5$ centrado en el$y$ eje.

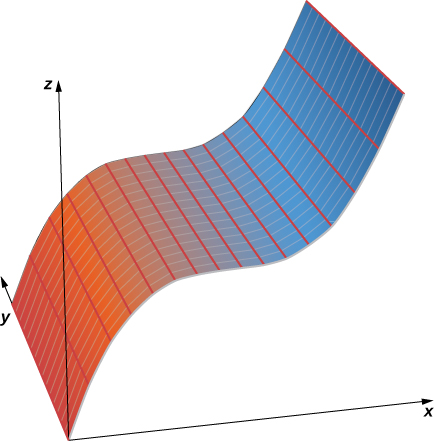
b. En este caso, la ecuación contiene las tres variables$ x,y,$ —y$ z$ —, por lo que ninguna de las variables puede variar arbitrariamente. La forma más fácil de visualizar esta superficie es usar una utilidad gráfica por computadora (Figura$\PageIndex{4}$).

Esta figura tiene una superficie en el primer octante. La sección transversal del sólido es una parábola. — Figura$\PageIndex{4}$

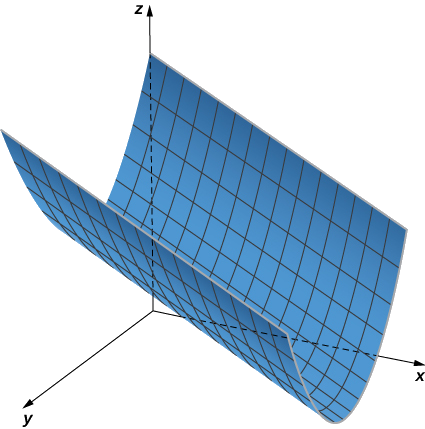
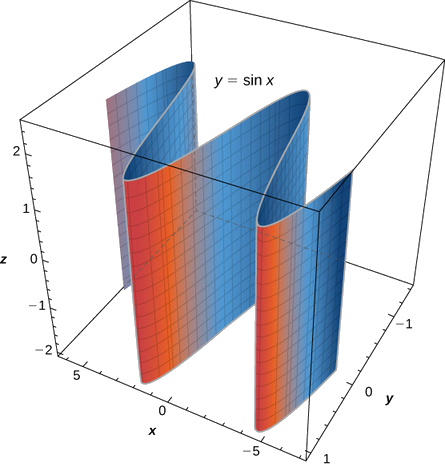
c. En esta ecuación, la variable$ z$ puede tomar cualquier valor sin límite. Por lo tanto, las líneas que componen esta superficie son paralelas al$z$ eje. La intersección de esta superficie con la curva de contornos de plano xy$ y=\sin x$ (Figura$\PageIndex{5}$).

Esta figura es una superficie tridimensional. Una sección transversal de la superficie paralela al plano x y sería la curva sinusoidal. — Figura$\PageIndex{5}$: La gráfica de la ecuación$ y=\sin x$ está formada por un conjunto de líneas paralelas al$z$ eje -que pasan por la curva$ y=\sin x$ en el$xy$ plano.

Ejercicio$ \PageIndex{1}$:

Haga un boceto o utilice una herramienta gráfica para ver la gráfica de la superficie cilíndrica definida por la ecuación$ z=y^2$.

Pista: La variable$ x$ puede tomar cualquier valor sin límite.
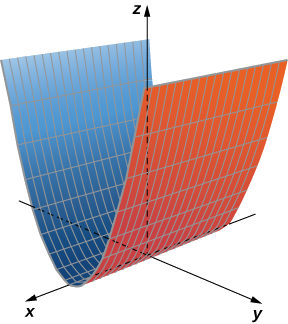
Contestar: $Esta figura es una superficie por encima del plano x y. Una sección transversal de esta superficie paralela al plano y z sería una parábola. La superficie se asienta en la parte superior del plano x y.$

Al esbozar superficies, hemos visto que es útil esbozar la intersección de la superficie con un plano paralelo a uno de los planos de coordenadas. Estas curvas se llaman trazas. Los podemos ver en la gráfica del cilindro en la Figura$\PageIndex{6}$.

Definición: traces

Las trazas de una superficie son las secciones transversales creadas cuando la superficie intersecta un plano paralelo a uno de los planos de coordenadas.

Las trazas son útiles para esbozar superficies cilíndricas. Sin embargo, para un cilindro en tres dimensiones, solo es útil un conjunto de trazas. Observe, en la Figura$\PageIndex{6}$, que la traza de la gráfica de$ z=\sin x$ en el plano xz es útil para construir la gráfica. La traza en el plano xy, sin embargo, es solo una serie de líneas paralelas, y la traza en el plano yz es simplemente una línea.

Esta figura tiene dos imágenes. La primera imagen es una superficie. Una sección transversal de la superficie paralela al plano x z sería una curva sinusoidal. La segunda imagen es la curva sinusoidal en el plano x y. — Figura$\PageIndex{6}$: (a) Esta es una vista de la gráfica de ecuación$ z=\sin x$. (b) Para encontrar el rastro de la gráfica en el$xz$ plano -plano, establecer$ y=0$. La traza es simplemente una onda sinusoidal bidimensional.

Las superficies cilíndricas están formadas por un conjunto de líneas paralelas. Sin embargo, no todas las superficies en tres dimensiones están construidas de manera tan simple. Ahora exploramos superficies más complejas, y las trazas son una herramienta importante en esta investigación.

Superficies cuadricas

Hemos aprendido sobre superficies en tres dimensiones descritas por ecuaciones de primer orden; estas son planos. Algunos otros tipos comunes de superficies pueden describirse mediante ecuaciones de segundo orden. Podemos ver estas superficies como extensiones tridimensionales de las secciones cónicas que discutimos anteriormente: la elipse, la parábola y la hipérbola. Llamamos a estas gráficas superficies cuádricas

Definición: Superficies cuádricas y secciones cónicas

Las superficies cuádricas son las gráficas de ecuaciones que se pueden expresar en la forma

\[Ax^2+By^2+Cz^2+Dxy+Exz+Fyz+Gx+Hy+Jz+K=0. \nonumber \]

Cuando una superficie cuádrica se cruza con un plano de coordenadas, el trazado es una sección cónica.

Un elipsoide es una superficie descrita por una ecuación de la forma$ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}=1.$ Set$ x=0$ para ver la traza del elipsoide en el plano yz. Para ver las huellas en los$xz$ planos$xy$ - y -conjuntos$ z=0$ y$ y=0$, respectivamente. Observe que, si$ a=b$, la traza en el$xy$ plano -es un círculo. Del mismo modo$ a=c$, si, la traza en el$xz$ plano -es un círculo y, si$ b=c$, entonces la traza en el$yz$ plano -es un círculo. Una esfera, entonces, es un elipsoide con$ a=b=c.$

Ejemplo$ \PageIndex{2}$: Sketching an Ellipsoid

Croquizar el elipsoide

\[ \dfrac{x^2}{2^2}+\dfrac{y^2}{3^2}+\dfrac{z^2}{5^2}=1. \nonumber \]

Solución

Comienza por bosquejar las huellas. Para encontrar la traza en el plano xy, establezca$ z=0: \dfrac{x^2}{2^2}+\dfrac{y^2}{3^2}=1$ (Figura$\PageIndex{7}$). Para encontrar las otras trazas, primero establece$ y=0$ y luego establece$ x=0.$

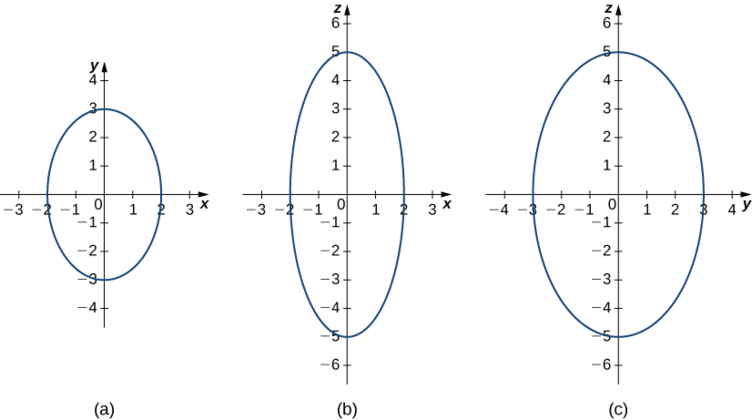
Esta figura tiene tres imágenes. La primera imagen es un óvalo centrado alrededor del origen del sistema de coordenadas rectangulares. Interseca el eje x en -2 y 2. Interseca el eje y en -3 y 3. La segunda imagen es un óvalo centrado alrededor del origen del sistema de coordenadas rectangulares. Interseca el eje x en -2 y 2 y el eje y en -5 y 5. La tercera imagen es un óvalo centrado alrededor del origen del sistema de coordenadas rectangulares. Interseca el eje x en -3 y 3 y el eje y en -5 y 5. — Figura$\PageIndex{7}$: (a) Esta gráfica representa la traza de ecuación$ \dfrac{x^2}{2^2}+\dfrac{y^2}{3^2}+\dfrac{z^2}{5^2}=1$ en el$xy$ plano -cuando establecemos$ z=0$. (b) Cuando establecemos$ y=0$, obtenemos el rastro del elipsoide en el$xz$ plano -que es una elipse. (c) Cuando establecemos$ x=0$, obtenemos el rastro del elipsoide en el$yz$ plano -que también es una elipse.

Ahora que sabemos cómo se ven las huellas de este sólido, podemos bosquejar la superficie en tres dimensiones (Figura$\PageIndex{8}$).

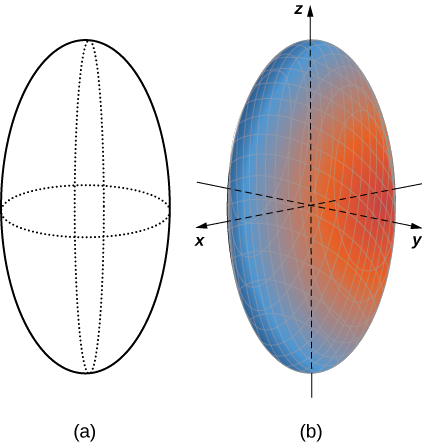
Esta figura tiene dos imágenes. La primera imagen es una elipse vertical. Hay dos curvas dibujadas con líneas discontinuas alrededor del centro horizontal y verticalmente para darle a la imagen una forma tridimensional. La segunda imagen es una forma elíptica sólida con el centro en el origen del sistema de coordenadas tridimensionales. — Figura$\PageIndex{8}$: (a) Las trazas proporcionan un marco para la superficie. b) El centro de este elipsoide es el origen.

La traza de un elipsoide es una elipse en cada uno de los planos de coordenadas. Sin embargo, este no tiene por qué ser el caso para todas las superficies cuádricas. Muchas superficies cuádricas tienen trazas que son diferentes tipos de secciones cónicas, y esto suele ser indicado por el nombre de la superficie. Por ejemplo, si una superficie puede describirse mediante una ecuación de la forma

\[ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=\dfrac{z}{c} \nonumber \]

entonces llamamos a esa superficie un paraboloide elíptico. La traza en el plano xy es una elipse, pero las trazas en el plano xz y en el plano yz son parábolas (Figura$\PageIndex{9}$). Otros paraboloides elípticos pueden tener otras orientaciones simplemente intercambiando las variables para darnos una variable diferente en el término lineal de la ecuación$ \dfrac{x^2}{a^2}+\dfrac{z^2}{c^2}=\dfrac{y}{b}$ o$ \dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}=\dfrac{x}{a}$.

Esta figura es la imagen de una superficie. Se encuentra en el sistema de coordenadas tridimensionales en la parte superior del origen. Una sección transversal de esta superficie paralela al plano x y sería una elipse. — Figura$\PageIndex{9}$: Esta superficie cuádrica se denomina paraboloide elíptico.

Ejemplo$ \PageIndex{3}$: Identifying Traces of Quadric Surfaces

Describir las huellas del paraboloide elíptico$ x^2+\dfrac{y^2}{2^2}=\dfrac{z}{5}$.

Solución

Para encontrar la traza en el$xy$ -plano, establezca$ z=0: x^2+\dfrac{y^2}{2^2}=0.$ La traza en el plano$ z=0$ es simplemente un punto, el origen. Dado que un solo punto no nos dice cuál es la forma, podemos ascender por el$z$ eje -hasta un plano arbitrario para encontrar la forma de otras trazas de la figura.

La traza en plano$ z=5$ es la gráfica de ecuación$ x^2+\dfrac{y^2}{2^2}=1$, que es una elipse. En el$xz$ plano -la ecuación se vuelve$ z=5x^2$. El rastro es una parábola en este plano y en cualquier plano con la ecuación$ y=b$.

En planos paralelos al$yz$ plano, las huellas también son parábolas, como podemos ver en la Figura$\PageIndex{10}$.

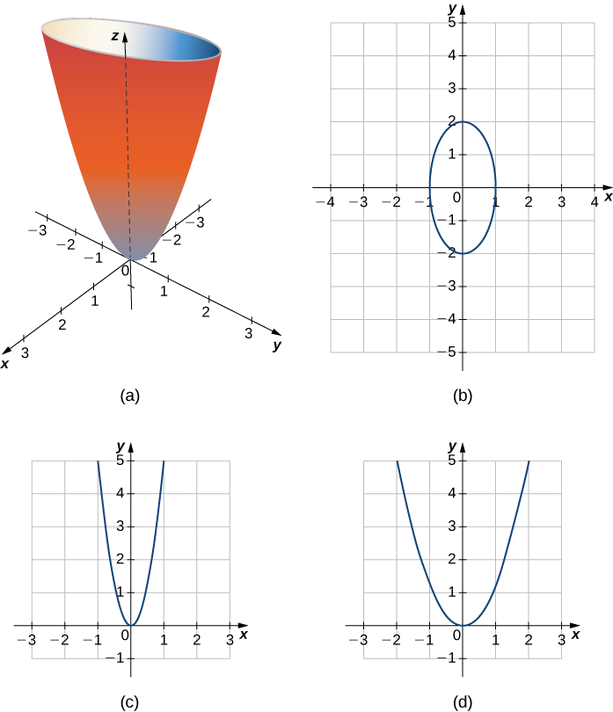
Esta figura tiene cuatro imágenes. La primera imagen es la imagen de una superficie. Se encuentra en el sistema de coordenadas tridimensionales en la parte superior del origen. Una sección transversal de esta superficie paralela al plano x y sería una elipse. Una sección transversal paralela al plano x z sería una parábola. Una sección transversal de la superficie paralela al plano y z sería una parábola. La segunda imagen es la sección transversal paralela al plano x y es una elipse. La tercera imagen es la sección transversal paralela al plano x z y es una parábola. La cuarta imagen es la sección transversal paralela al plano y z y es una parábola. — Figura$\PageIndex{10}$: (a) El paraboloide$ x^2+\dfrac{y^2}{2^2}=\dfrac{z}{5}$. b) El rastro en plano$ z=5$. c) El rastro en el$xz$ plano. d) El rastro en el$yz$ plano.

Ejercicio$ \PageIndex{2}$:

Un hiperboloide de una lámina es cualquier superficie que pueda describirse con una ecuación de la forma$ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1$. Describir las trazas del hiperboloide de una hoja dadas por la ecuación$ \dfrac{x^2}{3^2}+\dfrac{y^2}{2^2}−\dfrac{z^2}{5^2}=1.$

Pista

Para encontrar las trazas en los planos de coordenadas, establezca cada variable en cero individualmente.

Contestar

Las trazas paralelas al$xy$ plano son elipses y las trazas paralelas a los$yz$ planos$xz$ - y -son hipérbolas. Específicamente, la traza en el$xy$ plano -es elipse$ \dfrac{x^2}{3^2}+\dfrac{y^2}{2^2}=1,$ la traza en el$xz$ plano -es hipérbola$ \dfrac{x^2}{3^2}−\dfrac{z^2}{5^2}=1,$ y la traza en el$yz$ plano -es hipérbola$ \dfrac{y^2}{2^2}−\dfrac{z^2}{5^2}=1$ (ver la siguiente figura).

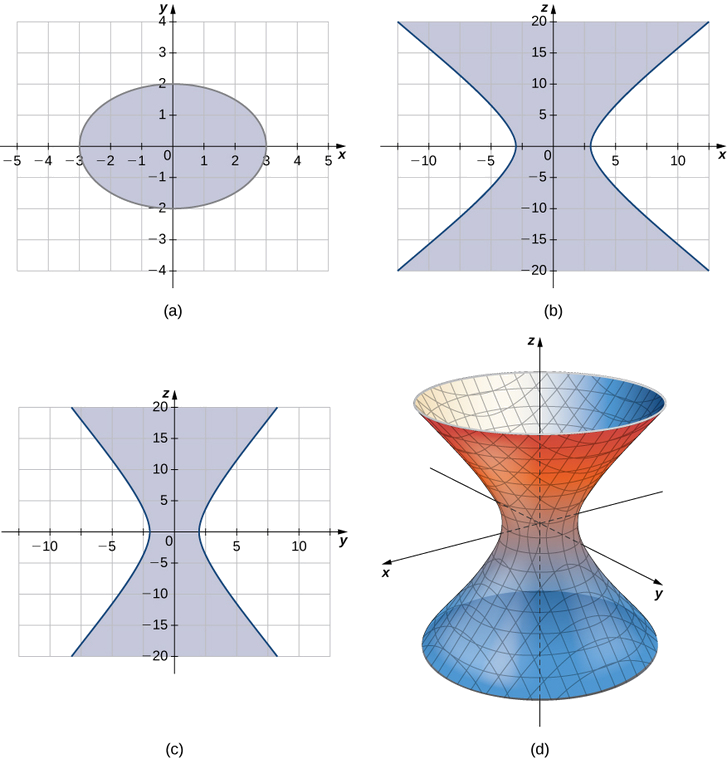
$Esta figura tiene cuatro imágenes. La primera imagen es una elipse centrada en el origen de un sistema de coordenadas rectangular. Interseca el eje x en -3 y 3. Interseca el eje y en -2 y 2. La segunda imagen es la gráfica de una hipérbola. Se trata de dos curvas, una abertura en la dirección x negativa y una simétrica en la dirección x positiva. La tercera imagen es la gráfica de una hipérbola en el plano y z. Se abre en la dirección y negativa y una curva simétrica que se abre en la dirección y positiva. La cuarta imagen es una superficie tridimensional. Sus secciones transversales superior e inferior serían circulares. Una intersección vertical sería una hipérbola.$

Los hiperboloides de una hoja tienen algunas propiedades fascinantes. Por ejemplo, se pueden construir usando líneas rectas, como en la escultura en Figura$\PageIndex{11a}$. De hecho, las torres de enfriamiento para centrales nucleares a menudo se construyen en forma de hiperboloide. Los constructores son capaces de utilizar vigas rectas de acero en la construcción, lo que hace que las torres sean muy fuertes mientras utilizan relativamente poco material (Figura$\PageIndex{11b}$).

Esta figura tiene dos imágenes. La primera imagen es una escultura hecha de palos paralelos, curvados juntos en un círculo con una sección transversal hiperbólica. La segunda imagen es una central nuclear. Las torres son de forma hiperbólica. — Figura$\PageIndex{11}$: (a) Una escultura en forma de hiperboloide puede construirse de líneas rectas. b) Las torres de enfriamiento para centrales nucleares suelen construirse en forma de hiperboloide.

Ejemplo$ \PageIndex{4}$: Chapter Opener: Finding the Focus of a Parabolic Reflector

La energía que golpea la superficie de un reflector parabólico se concentra en el punto focal del reflector (Figura$\PageIndex{12}$). Si la superficie de un reflector parabólico se describe por ecuación$ \dfrac{x^2}{100}+\dfrac{y^2}{100}=\dfrac{z}{4},$ ¿dónde está el punto focal del reflector?

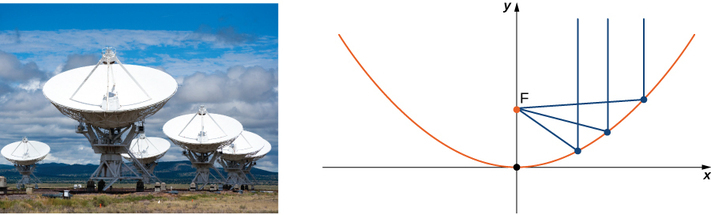
Esta figura tiene dos imágenes. La primera imagen es una imagen de antenas parabólicas con reflectores parabólicos. La segunda imagen es una curva parabólica sobre un segmento lineal. El fondo de la curva está en el punto V. Hay un segmento de línea perpendicular al otro segmento de línea a través de V. Hay un punto en este segmento de línea etiquetado F. Hay 3 líneas de F a la parábola, que se cruzan en P sub 1, P sub 2 y P sub 3. También hay tres líneas verticales de P sub 1 a Q sub 1, de P sub 2 a Q sub 2, y de P sub 3 a Q sub 3. — Figura$\PageIndex{12}$: La energía se refleja en el reflector parabólico y se recoge en el punto focal. (crédito: modificación de CGP Grey, Wikimedia Commons)

Solución

Dado que z es la variable de primera potencia, el eje del reflector corresponde al$z$ eje -eje. Los coeficientes de$ x^2$ and $ y^2$ are equal, so the cross-section of the paraboloid perpendicular to the $z$ -eje es un círculo. Podemos considerar una traza en el plano xz o en el plano yz; el resultado es el mismo. Ajuste$ y=0$, the trace is a parabola opening up along the $z$ del eje, con ecuación estándar$ x^2=4pz$, where $ p$ is the focal length of the parabola. In this case, this equation becomes $ x^2=100⋅\dfrac{z}{4}=4pz$ or $ 25=4p$. So p is $ 6.25$ m, which tells us that the focus of the paraboloid is $ 6.25$ m up the axis from the vertex. Because the vertex of this surface is the origin, the focal point is $ (0,0,6.25).$

Diecisiete superficies cuádricas estándar se pueden derivar de la ecuación general

\[Ax^2+By^2+Cz^2+Dxy+Exz+Fyz+Gx+Hy+Jz+K=0. \nonumber \]

En las siguientes cifras se resumen las más importantes.

Esta figura es de una tabla con dos columnas y tres filas. Las tres filas representan las primeras 6 superficies cuádricas: elipsoide, hiperboloide de una hoja e hiperboloide de dos láminas. Las ecuaciones y trazas están en la primera columna. La segunda columna tiene las gráficas de las superficies. La gráfica elipsoide es una forma redonda oblonga vertical. El hiperboloide de una hoja es circular en la parte superior e inferior y estrecho en el medio. El hiperboloide en dos láminas tiene dos cúpulas parabólicas opuestas entre sí. — Figura$\PageIndex{13}$: Características de las Superficies Cuádricas Comunes: Elipsoide, Hiperboloide de Una Hoja, Hiperboloide de Dos Hojas.

Esta figura es de una tabla con dos columnas y tres filas. Las tres filas representan las 6 segundas superficies cuádricas: cono elíptico, paraboloide elíptico y paraboloide hiperbólico. Las ecuaciones y trazas están en la primera columna. La segunda columna tiene las gráficas de las superficies. El cono elíptico tiene dos conos que tocan en los puntos. El paraboloide elíptico es similar a un cono pero oblongo. El paraboloide hiperbólico tiene una curva en el medio similar a una silla de montar. — Figura$\PageIndex{14}$: Características de las superficies cuádricas comunes: cono elíptico, paraboloide elíptico, paraboloide hiperbólico.

Ejemplo$ \PageIndex{5}$: Identifying Equations of Quadric Surfaces

Identificar las superficies representadas por las ecuaciones dadas.

$ 16x^2+9y^2+16z^2=144$
$ 9x^2−18x+4y^2+16y−36z+25=0$

Solución

a. los$ z$ términos$ x,y,$ y son todos al cuadrado, y todos son positivos, por lo que este es probablemente un elipsoide. Sin embargo, pongamos la ecuación en la forma estándar para un elipsoide solo para estar seguros. Tenemos

\[ 16x^2+9y^2+16z^2=144. \nonumber \]

Dividiendo por 144 da

\[ \dfrac{x^2}{9}+\dfrac{y^2}{16}+\dfrac{z^2}{9}=1. \nonumber \]

Entonces, esto es, de hecho, un elipsoide, centrado en el origen.

b. primero notamos que el$ z$ término se eleva solo a la primera potencia, por lo que este es un paraboloide elíptico o un paraboloide hiperbólico. También observamos que hay$ x$ términos y$ y$ términos que no son cuadrados, por lo que esta superficie cuádrica no está centrada en el origen. Necesitamos completar el cuadrado para poner esta ecuación en una de las formas estándar. Tenemos

\[ \begin{align*} 9x^2−18x+4y^2+16y−36z+25 =0 \\[4pt] 9x^2−18x+4y^2+16y+25 =36z \\[4pt] 9(x^2−2x)+4(y^2+4y)+25 =36z \\[4pt] 9(x^2−2x+1−1)+4(y^2+4y+4−4)+25 =36z \\[4pt] 9(x−1)^2−9+4(y+2)^2−16+25 =36z \\[4pt] 9(x−1)^2+4(y+2)^2 =36z \\[4pt] \dfrac{(x−1)^2}{4}+\dfrac{(y−2)^2}{9} =z. \end{align*}\]

Este es un paraboloide elíptico centrado en$ (1,2,0).$

Ejercicio$ \PageIndex{3}$

Identificar la superficie representada por la ecuación$ 9x^2+y^2−z^2+2z−10=0.$

Pista: Mira los signos y poderes de la$ x,y$, y$ z$ términos
Contestar: Hiperboloide de una hoja, centrado en$ (0,0,1)$.

Conceptos clave

Un conjunto de líneas paralelas a una línea dada que pasa por una curva dada se denomina cilindro, o superficie cilíndrica. A las líneas paralelas se les llama sentencias.
La intersección de una superficie tridimensional y un plano se llama traza. Para encontrar el rastro en los planos $xy$$yz$-, -, o$xz$ -, conjunto$ z=0,x=0,$ o$ y=0,$ respectivamente.
Las superficies cuádricas son superficies tridimensionales con trazas compuestas por secciones cónicas. Cada superficie cuádrica se puede expresar con una ecuación de la forma

\[Ax^2+By^2+Cz^2+Dxy+Exz+Fyz+Gx+Hy+Jz+K=0. \nonumber \]

Para bosquejar la gráfica de una superficie cuádrica, comience por esbozar las trazas para comprender el marco de la superficie.
Las superficies cuádricas importantes se resumen en Figuras$\PageIndex{13}$ y$\PageIndex{14}$.

Glosario

cilindro: un conjunto de líneas paralelas a una línea dada que pasa por una curva dada

elipsoide: una superficie tridimensional descrita por una ecuación de la forma$ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}=1$; todas las trazas de esta superficie son elipses

cono elíptico: una superficie tridimensional descrita por una ecuación de la forma$ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=0$; las trazas de esta superficie incluyen elipses y líneas de intersección

paraboloide elíptico: una superficie tridimensional descrita por una ecuación de la forma$ z=\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}$; las trazas de esta superficie incluyen elipses y parábolas

hiperboloide de una hoja: una superficie tridimensional descrita por una ecuación de las$ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1;$ trazas de forma de esta superficie incluyen elipses e hipérbolas

hiperboloide de dos hojas: una superficie tridimensional descrita por una ecuación de la forma$ \dfrac{z^2}{c^2}−\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1$; las trazas de esta superficie incluyen elipses e hipérbolas

superficies cuádricas: superficies en tres dimensiones que tienen la propiedad de que las trazas de la superficie son secciones cónicas (elipses, hipérbolas y parábolas)

dictámenes: líneas paralelas que conforman una superficie cilíndrica

trazar: la intersección de una superficie tridimensional con un plano de coordenadas

Search

Text Color

Text Size

Margin Size

Font Type

Definición: cilindros y resoluciones

Ejemplo\( \PageIndex{1}\): Graphing Cylindrical Surfaces

Ejercicio\( \PageIndex{1}\):

Definición: traces

Definición: Superficies cuádricas y secciones cónicas

Ejemplo\( \PageIndex{2}\): Sketching an Ellipsoid

Ejemplo\( \PageIndex{3}\): Identifying Traces of Quadric Surfaces

Ejercicio\( \PageIndex{2}\):

Ejemplo\( \PageIndex{4}\): Chapter Opener: Finding the Focus of a Parabolic Reflector

Ejemplo\( \PageIndex{5}\): Identifying Equations of Quadric Surfaces

Ejercicio\( \PageIndex{3}\)