8: Compuestos conjugados y aromaticidad

Conjugación: Conjugación es el término que usamos para describir una disposición de enlaces simples y dobles alternantes. Para explicar cómo se comportan los sistemas conjugados de manera diferente a los sistemas no conjugados compararemos 1,3-pentadieno (que está conjugado) y 1,4 pentadieno (que no está conjugado). Para reconocer las diferencias entre ambos, veamos los orbitales que están involucrados en la vinculación del$\pi$ sistema. Recordemos que$\pi$ los enlaces pueden considerarse como la superposición de lado a lado de p orbitales, de manera que la densidad de electrones se encuentra por encima y por debajo del plano del resto de la molécula. Consideremos los orbitales en 1,3-pentadieno: hay superposición de$\mathrm{p}$ orbitales que resultan en un continuo

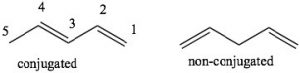
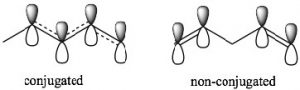
π sistema orbital sobre carbonos 1-4. La consecuencia de esto es que existe algún carácter parcial de doble enlace entre los carbonos 2 y 3. En el 1,4-pentadieno no hay posibilidad de solapamiento entre los dos$\pi$ enlaces separados. Nótese que en el sistema no conjugado, existe un carbono$\mathrm{sp}^{3}$ hibridado entre los dos conjuntos de dobles enlaces carbono-carbono$\mathrm{sp}^{2}$ hibridados lo que evita cualquier superposición de ($\mathrm{p}$) orbitales en los carbonos 2 y 4.

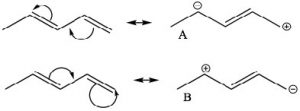
Una forma de indicar y predecir dónde puede ocurrir este carácter de doble enlace parcial es usar estructuras de resonancia. Podemos escribir estructuras de resonancia para el sistema conjugado que tienen carácter de doble enlace entre$\mathrm{C}-2$ y$\mathrm{C}-3$. Tenga en cuenta que dado que los contribuyentes de resonancia A y B son equivalentes, no hay separación de carga real en esta molécula. No es posible (sin romper un enlace sigma) escribir estructuras de resonancia como esta para 1,4-pentadieno (intenta convencerte de que esto es cierto).

Teoría Orbital Molecular: Otro modelo que se puede utilizar para describir la unión es considerar el sistema π en términos de teoría orbital molecular. La teoría orbital molecular considera que los orbitales de unión se extienden sobre toda la molécula. El número de orbitales moleculares es igual a la suma de todos los orbitales atómicos. En la práctica, este enfoque es demasiado complejo incluso para la más pequeña de las moléculas orgánicas, por lo que solemos utilizar el modelo de enlace de valencia más simple en el que consideramos que los enlaces se encuentran entre dos átomos. En el caso de sistemas conjugados, a menudo es útil usar el enfoque de enlace de valencia para el marco sigma (enlaces simples) y luego considerar el sistema π conjugado usando la teoría orbital molecular. En este caso, si tenemos un sistema conjugado de dos enlaces π, entonces cuatro orbitales atómicos p están involucrados en la formación de los cuatro orbitales moleculares.$\mathrm{MO}$ Recordemos que cuando los orbitales moleculares se forman a partir de orbitales atómicos, si las funciones de onda (mecánica cuántica)$\mathrm{MO}$ se suman en fase, la energía resultante de la es más baja, es decir, la$\mathrm{MO}$ interacción$\mathrm{MO}$ se estabiliza y la$\mathrm{AO}$ s se une s.$\mathrm{AO}$ , la interacción es desestabilizante y el resultado es antiligante$\mathrm{MO}$ s. Nótese que, en el diagrama ($\downarrow$), solo la energía más baja$\mathrm{MO}$ tiene densidad de electrones entre los carbonos 2 y 3. Todos los demás$\mathrm{MO}$ s tienen un nodo (sin densidad electrónica) en esta posición. En general, vemos que hay más densidad de$\pi$ electrones entre$\mathrm{C}-1$ y$\mathrm{C}-2$, y entre$\mathrm{C}-3$ y$\mathrm{C}-4$.

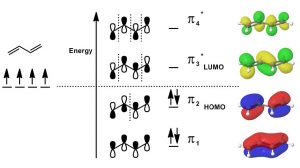
Dado que solo hay 4$\pi$ electrones, solo los dos enlaces$\mathrm{MO}$ están ocupados mientras que los dos antiligantes$\mathrm{MO}$ están desocupados. Como veremos, si consideramos reacciones usando$\mathrm{MO}$ teoría, los Ocupados Más Altos$\mathrm{MO}$ ($\mathrm{HOMO}$) y los Desocupados Más Bajos$\mathrm{MO}$ ($\mathrm{LUMO}$) son los orbitales que participan en nuevas interacciones de vinculación. En general, utilizamos el modelo más simple que nos permite predecir y explicar el resultado de las reacciones, que suele ser la teoría del vínculo de valencia, pero recurriremos a la$\mathrm{MO}$ teoría cuando sea necesario, y las discusiones sobre sistemas conjugados a veces requieren$\mathrm{MO}$ teoría para explicar fenómenos.

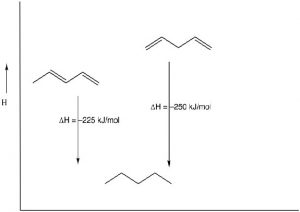
Estabilidad de Sistemas Conjugados: Como hemos visto antes, una forma de identificar la estabilidad termodinámica de los alquenos es reducirlos al alcano correspondiente añadiendo$\mathrm{H}_{2}$ (hidrógenos) a través del doble enlace y determinar el cambio de entalpía. ^[1] En el caso del 1,3- y 1,4-pentadieno, podemos comparar sus calores de hidrogenación para producir el pentano correspondiente; encontramos que el dieno conjugado es aproximadamente$25 \mathrm{kJ/mol}$ más estable. Este es un hallazgo general: cuanto más conjugado es un sistema, más estable es y menos reactivo es.